Pytorch 多项式回归

一、一般的多项式回归模型：

$y=\beta_{0}+\beta_{1} x+\beta_{2} x^{2}+\beta_{3} x^{3}+\cdots+\beta_{n} x^{n}+\varepsilon$

$\left[\begin{array}{c}y_{1} \\ y_{2} \\ y_{3} \\ \vdots \\ y_{n}\end{array}\right]=\left[\begin{array}{ccccc}1 & x_{1} & x_{1}^{2} & \ldots & x_{1}^{m} \\ 1 & x_{2} & x_{2}^{2} & \ldots & x_{2}^{m} \\ 1 & x_{3} & x_{3}^{2} & \ldots & x_{3}^{m} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n} & x_{n}^{2} & \ldots & x_{n}^{m}\end{array}\right]\left[\begin{array}{c}\beta_{0} \\ \beta_{1} \\ \beta_{2} \\ \vdots \\ \beta_{m}\end{array}\right]+\left[\begin{array}{c}\varepsilon_{1} \\ \varepsilon_{2} \\ \varepsilon_{3} \\ \vdots \\ \varepsilon_{n}\end{array}\right]$

 

二、步骤及代码

因此，首先我们需要将输入 [x1, x2, ..., xn] 转变成矩阵 $\left[\begin{array}{ccccc}1 & x_{1} & x_{1}^{2} & \ldots & x_{1}^{m} \\ 1 & x_{2} & x_{2}^{2} & \ldots & x_{2}^{m} \\ 1 & x_{3} & x_{3}^{2} & \ldots & x_{3}^{m} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n} & x_{n}^{2} & \ldots & x_{n}^{m}\end{array}\right]$，构造如下函数：

def make_features(x):
    x = x.unsqueeze(1)
    return torch.cat([x**i for i in range(0,4)],1)

传入参数x是n维向量tensor([x1,x2,...,xn]),

x.unsqueeze(1)：返回一个新的张量，对输入的既定位置插入一个新维度, 既定位置通过传入参数dim = n (0,1,2,...)指定。

                           传入参数1代表的是参数dim=1，按行unsqueeze；dim=0是按列unsqueeze

                           1. 当x是一个向量：

dim = 1:        dim = 0:    

dim = 2:            

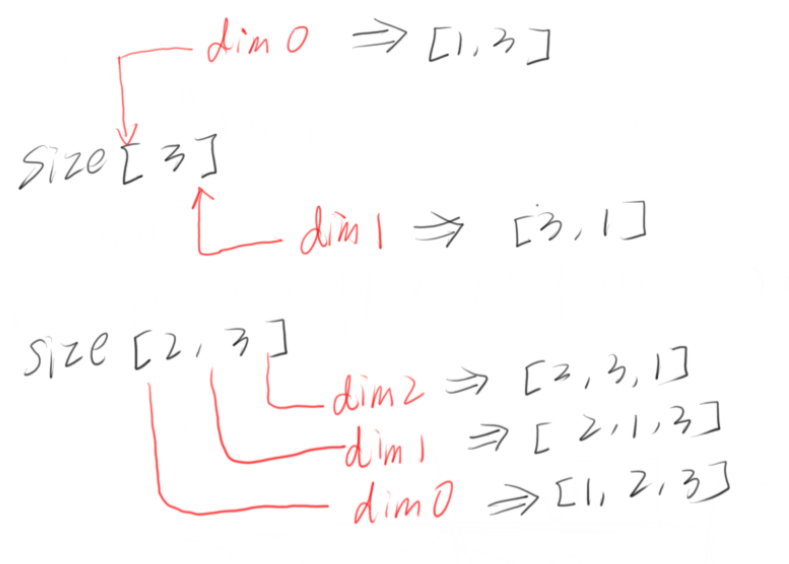
因此这个程序，就是把size[n]的tensor变成size[n,1]的tensor，之后再用torch.cat()按列连接起来。

 

torch.cat([x**i for i in range(0,4)],1)：

x是一个tensor, x**i运算是把x里每一个数都执行**i运算。1指的是dim=1，把x**i放在列上。

定义真实的函数：

def f(x):
    w_target = torch.FloatTensor([0.9,0.5,3,2.4]).unsqueeze(1)
    return x.mm(w_target)

其中：0.9-ε, 0.5-β1, 03-β2, 2.4-β3

x.mm(w_target) 和 x@w_target 一样，都是矩阵乘法

 

随机生成一些独立同分布的点：

def get_batch(batch_size=32):
    random = torch.randn(batch_size)
    x = make_feature(random)
    y = f(x)
    return x,y

torch.randn(*size, out=None)：返回一个张量，包含了从标准正态分布（均值为0，方差为1，即高斯白噪声）中抽取的一组随机数。张量的形状由参数sizes定义。size是整数序列，例如torch.randn(32)就是返回size[32]的32维向量；torch.randn(2,3)返回size[2,3]的矩阵。

 

构建模型：

class Poly_Regression(nn.Module):
    def __init__(self):
        super().__init__()
        self.poly = nn.Linear(4,1)
        
    def forward(self,x):
        out = self.poly(x)
        return out

 

实例化模型：

if torch.cuda.is_available():
    model = Poly_Regression().cuda()
else:
    model = Poly_Regression()

 

选择损失函数，优化器：

loss_fn = nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(),lr=0.001)

 

训练模型：

epoch = 0
loss_val = 1

while loss_val>0.001:
    batch_x, batch_y = get_batch()
    pred = model(batch_x)
    loss = loss_fn(pred,batch_y)
    loss_val = loss.item()
    
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    
    if epoch%100 == 0:
        print(f'Loss: {loss_val} after {epoch} batches.')
    
    epoch += 1
    
print(f'Loss: {loss_val} after {epoch} batches.')