Minkowski (Manhattan, Euclidean, Chebyshev) distance, Mahalanobis distance, cosine distance

1. Minkowski distance

$D(x, y)=\left(\sum_{u=1}^{n}\left|x_{u}-y_{u}\right|^{p}\right)^{\frac{1}{p}}$

 

(1) Manhattan distance

$d(x, y)=\sum_{i=1}^{n}\left|x_{i}-y_{i}\right|$

"Manhattan distance" is named by Minkowski and is derived from the layout of Manhattan city's blocks. It represents a total distance summed up by distances along the axes (in the following graph, there're two axes x, y, the red line is Manhattan distance, the blue and yellow line are two varieties of Manhattan distance, plus, the green line is Euclidean distance. )

The weight of each feature parameter is equal.。

 

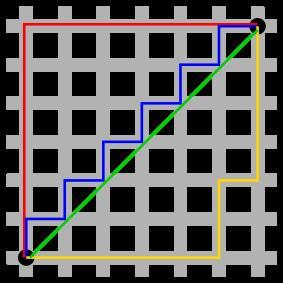
(2) Euclidean distance

$d(x, y)=\sqrt{\sum_{i=1}^{n}\left(x_{i}-y_{i}\right)^{2}}$

"Euclidean distance" is based on normal concept of "distance".

The weight of each feature parameter is equal.

For most statistical problems, it is not satisfying because it has two defects:

① when a feature $x_{i}$ is measured by some ways, it has error/noise inevitably. And different $x_{i}$ have error/noise of different magnitude

② When the components are quantities of different properties (such as $x_{1}$ is in m, $x_{2}$ is in s), the Euclidean distance should be effected by unit of measurement ?!

 

 (3) Standardized Euclidean distance

$d(x,y)=\sqrt{\sum_{i=1}^{N} \frac{\left(x_{i}-y_{i}\right)^{2}}{s_{i}^{2}}}$

 when taking variances on corresponding features into consideration, the unit of measurement would be irrelevant.

 

(4) Chebyshev distance

 Let $p \rightarrow \infty$, we can get Chebyshev distance $D(x,y)=\max _{i}\left(\left|x_{i}-y_{i}\right|\right)$

Chebyshev distance is only used in a few specific situations.

 

2. Mahalanobis distance

the Mahalanobis distance berween X and Y is:

$D_{m}(x, y)=\sqrt{(x-y)^{T} \Sigma^{-1}(x-y)}$

where X and Y are two samples from a same sample space with mean vector $\mu$ and covarriance matrix $\Sigma$

Compared with standardized Euclidean distance, Mahalanobis distance take covariance of different features into consideration.

An example: there are two category: 1. $\mu=0, \delta=0.1$ 2. $\mu=10, \delta=5$, and there is one point: $x=2$

from Euclidean distance, x is near to category 1, because it doesn't count $\delta$.

However, from our normal understanding, x is more likely to br category 2, because we consider the $\delta_{1}$, so $x_{1}$ can hardly reach 2.

 

3. Cosine distance (Cosine similarity)

First, cosine distance is more like a "simliarity" rather than a "distance", 

similarity $=\cos (\theta)=\frac{A \cdot B}{\|A\|\|B\|}=\frac{\sum_{i=1}^{n} A_{i} \times B_{i}}{\sqrt{\sum_{i=1}^{n}\left(A_{i}\right)^{2}} \times \sqrt{\sum_{i=1}^{n}\left(B_{i}\right)^{2}}}$

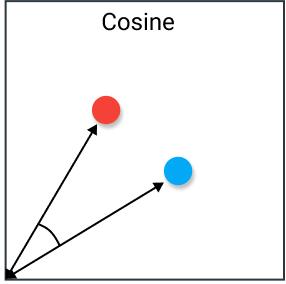
when $\theta=0$, the similarity is 1, that is to say this two vector are totally same is this feature.

Similarly, $\theta=180$, --> opposite

 

 

Reference List:

https://zhuanlan.zhihu.com/p/46626607

https://www.thepaper.cn/newsDetail_forward_11338779

https://blog.csdn.net/weixin_42056745/article/details/80583707