中学数学的公理化探索
前言
笔者高一。退役oier。痛苦的补文化课中。此处是一些游离于课堂之外的探索。全文 \(4500\) 字。
感觉我的 \(Markdown\) 比之前好多了!!!
看到课本定理十分杂乱(其实高中课本还好),只在部分地方给出了证明。因此无法仅由简单的公理演绎推理出体系。
数学的公理化。实际上,这也是现代中学的一大项工作。但除了中学阶段,我感觉做这项事情意义不大。定理数目如此庞大,光是识记都很难全部接触。一个人穷尽一生,大概也只能摸透一两个小分支罢了。甚至包括中学阶段,做这件事对学业的帮助近乎为零。可能我也只是闲的蛋疼。但他无用吗?不尽然。在不断的抽象当中,我们了解到本质,从而才能推知其他知识。
看到没大有人做这些工作,笔者在初三做了些研究,大概在中学数学体系下,我给到的这些公理能够推知大部分中学定理。只要公理无误,建立在其上的证明和理论都能经得起推敲(?)。
害,说到底还是古代数学太简单了。我现在做了这么多的工作,在现代数学眼前,相当于制作了0-1,其实并没什么用。我猜测这就是中学强调解题技巧的原因了吧。说到底还是站在前人的肩膀上舒服~
公理化体系
几何
首先是几何的公理化。即欧几里得的假设。
-
点不可再分割。
-
线只有长度而没有宽度。
-
线的两端是点。
-
直线是它上面的线一样地平铺的线。
-
面只有长度和宽度。
-
面的边是线。
-
平面是它上面的线一样地平铺的线。
-
平面角是在一个平面内但不在一条直线上的两条相交线相互的倾斜度。
-
当含有角的两条线成一条直线时,这个角称为平角。
-
当一条直线和另一条直线交成的邻角彼此相等时,这些角的每一个叫做直角,而且称这一条直线垂直于另一条直线。
-
当一个角大于直角时,该角为钝角。
-
当一个角小于直角时,该角为锐角。
-
边界是物体的边缘。
-
图形是由一个边界或几个边界所围成的。
-
圆是由一条线围成的平面图形,其内有一点与这条线上的点连接的所有线段都相等。
-
而且把这个点叫做圆心。
-
圆的直径是任意一条经过圆心的直线在两个方向被圆周截得的线段,且把圆二等分。
-
半圆是直径和由它截得的圆周所围成的图形,而且半圆的心和圆心相同。
-
直线形是由直线所围成的,三边形是由三条直线围成的,四边形是由四条直线围成的,多边形是由四条以上直线围成的。
-
在三边形中,三条边相等的,叫做等边三角形;只有两条边相等的,叫做等腰三角形;各边不等的,叫做不等边三角形。
-
此外,在三边形中,有一个角是直角的,叫做直角三角形;有一个角是钝角的,叫做钝角三角形;有三个角是锐角的,叫做锐角三角形。
-
在四边形中,四边相等且四个角是直角的,叫做正方形;角是直角,但四边不全相等的,叫做长方形;四边相等,但角不是直角的,叫做菱形;对角相等且对边也相等,但边不全相等且角不是直角的,叫做平行四边形;其余四边形叫做不规则四边形。
-
平行直线是在同一个平面内的一些直线,向两个方向无限延伸,在不论哪个方向他们都不相交。
可以看到,我是照搬的欧几里得几何原本中的定义。这是给出一些几何事物的定义。由于翻译问题,术语略有不同,譬如三边形,平行直线,分别叫做三角形,平行线。
初中教材给出的平行线定义是:
给出一条直线及不在这条直线上的一个点,至多可以画一条直线通过已知点并且平行于这条直线。等价的,可以自己证证。
下面是公设:
- 任意两点可以连成一条直线;
- 有限直线可以无限延伸;
- 以任意点为圆心,任意长度为半径,可以画出一个圆;
- 所有直角相等;
- 如果一条直线与两条直线相交,且内角之和小于两直角,那么这两条直线在这一侧必然相交。
前三条给到了直线的性质,圆的性质。实际上如果去读原著,这三条起到的作用十分之大。
还有关于等式的:
-
等于同量的量彼此相等。
-
等量加等量,其和仍相等。
-
等量减等量,其差仍相等。
-
彼此能够重合的物体是全等的。
-
整体大于部分。
自这里衔接初一平行线相关内容,初二平几内容。
给一下第一个定理,看一下如何巧妙运用:
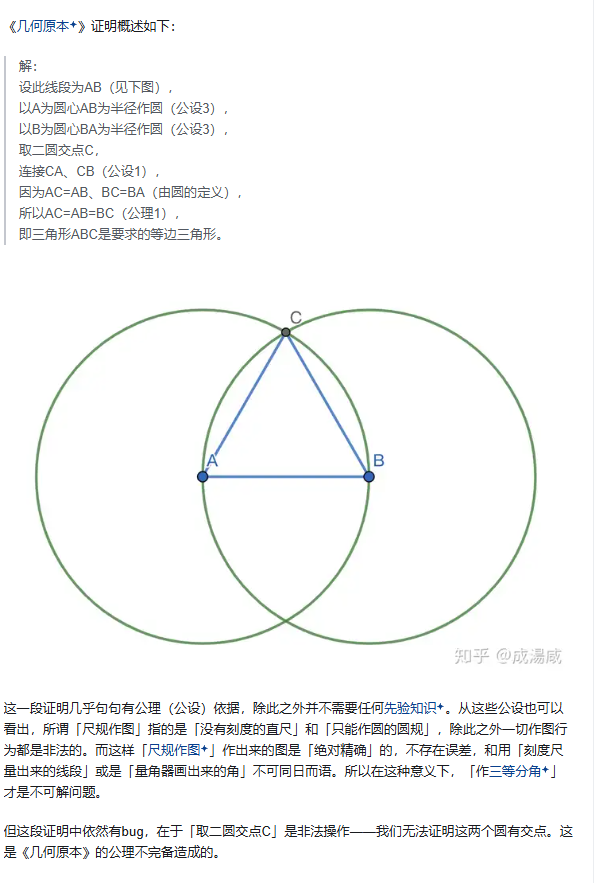
你可能会注意到,两点之间线段最短之类没有列为公理,如何证明?

那么其实就证出来了啊。两点之间,线段最短。
具体的可以去读几何原本,越读发现自己越惊叹于现代数学的符号语言。现代数学的符号语言真是太简便了,那个翻译的又臭又长。
代数
集合:
熟知的是 \(ZFC\) 公理。但我觉得对高中数学过于冗杂,做此简化(实际上是复杂化了,但我也没办法,高中用不到那么基础),实际上大部分定理是能推得。
- 元素是任何事物。集合由许多元素构成。一个集合完全由其元素决定。
- 不存在集合成为另一个集合的元素。
- 元素与集合:参与构成集合的元素属于(\(\in\))集合。反之不属于。
- 集合的二元关系之相等:拥有相同的元素,称为集合相等(\(=\))。
- 空集是没有元素的集合。且总有集合存在,空集存在。
- 集合的二元关系之并:两集合参与并(\(\cup\))运算,运算结果是一个集合,且对于两个运算集合的任意元素都属于此集合。
- 集合的二元关系之交:两集合参与交(\(\cap\))运算,运算结果是一个集合,且对于两个运算集合的共同元素都属于此集合。
- 集合二元关系之子集:如果集合 \(A\) 的任意一个元素都是集合 \(B\) 的元素,那么集合 \(A\) 称为集合 \(B\) 的子集。若不等,称作真子集。
- 上述二元关系对任意集合都存在。
- 存在无穷大小的集合。且与任何集合并的结果都是无限集。
后续可以看高中课本了。都是小推论了。另外,上述公理我在给出时直接不讨论理发师悖论。因此我相当于把集合原本定义缩窄了,但不影响高中学习。
下面出场的是数:
我首先对自然数给到定义:
-
\(0\) 是自然数;
-
每一个确定的自然数 \(a\),都有一个确定的后继数 \(a'\) ,\(a'\) 也是自然数;
-
对于每个自然数\(b、c\),\(b=c\) 当且仅当 \(b\) 的后继数 \(=c\)的后继数;
-
\(0\) 不是任何自然数的后继数;
-
任意关于自然数的命题,如果证明:它对自然数 \(0\)是真的,且假定它对自然数 \(a\) 为真时,可以证明对 \(a'\) 也真。那么,命题对所有自然数都真。)
这其实就是皮亚诺公理。精华在最后一条。这个归纳实在是太强了。
他可以证明 \(1+1=2\), 只需要用到下面的运算hhh,多年的疑惑解开了。
关于实数的引入,https://baike.baidu.com/item/实数公理 。
其实我也没太看明白,但是大概上就是拿性质去框这个数。
关于复数,呃呃由于我还没学到,不讨论了。
下面出场的是运算:
这个东西叫代数系统。实际上就是一堆定义。喜欢的可以直接搜索,笔者做如下简化(复杂化。功力有限):
不是准确定义!!!本人功力不足,尚且只能满足高中需求罢了。
\(n\) 元运算是从一个集合\(A\) 抽取 \(n\) 个元素做某种对应关系 \(f\),对应一个元素,在此基础上取遍所有可能,所对应元素形成集合 \(B\),则是 \(f: A^n → B\)。
由于一元运算(例如\(!x\))和多元运算(例如 \(A?B:C\))较为少见,我们只讨论二元运算。
从这里看出来,函数和运算有着不可分割的联系。https://www.zhihu.com/question/427870114
下面给出定义。你就会发现,所有的运算的共性。
对于 \(f: A^2 → B\), 任取做运算两个数 \(a, b\), 结果为 \(c\)。姑且写作 \(a * b=c\):
- 若 \(B=A\), 叫做封闭律。
- 若 \(a*b=b*a\),满足交换律。
- 若 \((a*b)*c=a*(b*c)\), 满足结合律。
- \(𝛥\)是另外一个运算,对于任意的 \(𝑎, 𝑏, 𝑐 ∈ 𝐴\),若有:
(1) \(𝑎 ∗ (𝑏𝛥𝑐) = (𝑎 ∗ 𝑏)𝛥(𝑎 ∗ 𝑐)\)
(2) \((𝑏𝛥𝑐) ∗ 𝑎 = (𝑏 ∗ 𝑎)𝛥(𝑐 ∗ 𝑎)\)
称 \(∗\) 对 \(𝛥\) 满足分配律.
如果只有(1)式成立, 那么称 \(∗\) 对 \(𝛥\)满足左分配律.
如果只有(2)式成立, 那么称∗对𝛥满足右分配律.
运算规律大致由这么几条,我们学过的无论加减乘除变换导积都或多或少满足以上规律。
https://www.zhihu.com/question/285971671
感性理解,封闭律就是怎么运算都跑不出去,交换律就是可以随意调换运算的数的顺序,结合律就是结果与括号打法无关。分配律就是连接两个运算的桥梁。从这个角度来说,结合律比交换律更本质。https://www.zhihu.com/question/536098304
比如:加法满足封闭律,交换律,乘法对加法有分配律。
关于结合律很多人不知道的冷知识:
函数复合也满足结合律!!!
先举几个结合律例子,
从这里就可以挖掘出超级多运算性质,同样的由于挖的太基础了,共性就更少。另外这里没有提及单位元,逆元等内容,因为用不到。
能导出什么?
当人们开始思考整数乘法时,一门伟大(dan teng)的学科就产生了。----数论。不展开。
下面是关于方程:
https://v.douyin.com/FH8PuKh/ 特别推荐此视频!!!我看了不下10遍。揭示了解方程的本质。

答案就在视频中。无需多言。我把最关键的一句截了出来。
关于组合:https://zhuanlan.zhihu.com/p/29151426
此文章把组合和集合联系了起来。
后记
本文不过是把早些时候做的工作近期整理一下。
写完了。感觉自己做了这么多工作,又好像没做。想自己写但是写的就是没有前人完善,所以此文才大篇幅引用。好像没什么意义。
我发现个神奇的东西:做着做着这些工作,我的数学直觉突然消失了。就是看什么都没有那么显然。去请教过这个问题。其实这很正常,是重建数学直觉的过程,其本质就是把这些推导变成直觉。
因为本文采取的公理化体系过于古老,因此这不是现代公理化的内容,但想学习现代公理化仍然需要以此作为跳板。比如本文采取欧几里得的公理体系,但后来被希尔伯特进行了重新定义。但是希尔伯特那本书基础的全没有(笑),可能还是要从欧几里得开始。近代也有研究欧氏几何的,可以继续研究,但是对中高考就没什么用了,(额可能数竞会有用?但是我好像对 \(MO\) 没那么感冒)。之所以选择几何原本而不是近欧,是因为我就是为了探索公理化体系,而不是更期望做题。
仅此而已了。

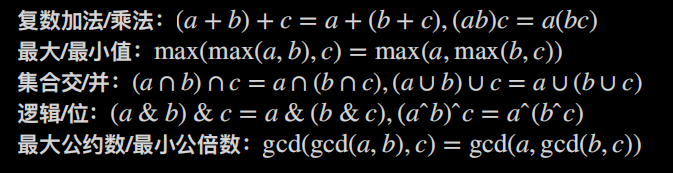
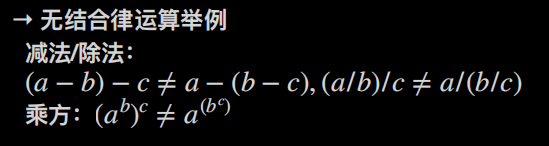

 浙公网安备 33010602011771号
浙公网安备 33010602011771号