【深度学习数学基础：高等数学】【苏德矿高等数学】第11讲：海涅定理

3. 函数极限

3.1 函数极限的概念

3.1.2 函数极限的性质

【例】\(f(x)=\left\{\begin{array}{ll} x+\sqrt{1+x^{2}}, & x<1 \\ x^{2}+2, & x \geqslant 1 \end{array}\right.\)，研究\(f(x)\)在\(x=1\)处极限是否存在。
【解】\(\lim\limits_{x\to 1^{-}}f(x)=\lim\limits_{x\to 1^{-}}(x+\sqrt{1+x^2})=1+\sqrt{2}\)
\(\lim\limits_{x\to 1^{+}}f(x)=\lim\limits_{x\to 1^{+}}(x^2+2)=3\)
由\(1+\sqrt{2}\ne 3\)知\(\lim\limits_{x\to 1}f(x)=\)不存在。

【例】\(f(x)=\left\{\begin{array}{ll} 1+x^2+3x^4, & x<0 \\ 1-x^3+x^5, & x \geqslant 0 \end{array}\right.\)，研究\(f(x)\)在\(x=0\)处极限是否存在？若存在，求极限。
【解】\(\lim\limits_{x\to 0^{-}}f(x)=\lim\limits_{x\to 0^{-}}(1+x^2+3x^4)=1\)
\(\lim\limits_{x\to 0^{+}}f(x)=\lim\limits_{x\to 0^{+}}(1-x^3+x^5)=1\)
由于\(1=1\)，所以\(\lim\limits_{x\to 0}f(x)=1\).

3.1.3 海涅定理

前置知识

【定理】\(\lim\limits_{n\to\infty}a_n=a\)，则\(\lim\limits_{n\to\infty}|a_n|=|a|\)，但反之不正确，但\(a=0\)时，反之也成立。
【证明】由\(\lim\limits_{n\to\infty}a_n=a\)，则\(\forall\varepsilon>0,\exists N\)，当\(n>N\)时，都有\(|a_n - a|<\varepsilon\)，而\(||a_n|-|a||<|a_n - a|<\varepsilon\)，从而\(n>N\)时，都有\(||a_n|-|a||<\varepsilon\)，所以\(\lim\limits_{n\to\infty}|a_n|=|a|\)，反之
当\(a=0\)时，由于\(\lim\limits_{n\to\infty}|a_n|=0\)，则\(\forall\varepsilon>0,\exists N\)，当\(n>N\)时，都有\(||a_n|-|0||<\varepsilon\)，即\(||a_n|-|0||=|a_n|=|a_n-0|<\varepsilon\)，则\(\lim\limits_{n\to\infty}a_n=0\)，此时反之也成立；
当\(a\ne 0\)时，举反例，由于\(\lim\limits_{n\to\infty}|(-1)^n|=\lim\limits_{n\to\infty}1=1\)，但\(\lim\limits_{n\to\infty}(-1)^n\)不存在，此时反之不成立。

海涅定理证明

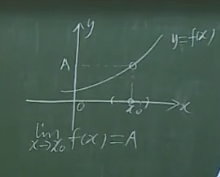
\(\lim\limits_{\to x_0}f(x)=A\)，在邻域中取一个数列包含于空心邻域（任给的数列），\(\left\{x_{n}\right\} \subset \stackrel{o}{U}\left(x_{0}\right)\)，\(\lim\limits_{n\to\infty}x_n=x_0\)
【定理】【海涅定理】【归结原则】\(\lim\limits_{x\to x_0}f(x)\)存在的充要条件是\(\forall\{x_n\} \subset \stackrel{o}{U}\)且\(\lim\limits_{n\to\infty}x_n=x_0\)，则\(\lim\limits_{n\to\infty}f(x_n)\)的极限均存在且相等。

【注】且相等是指，这些若干个\(\{f(x_n)\}\)的数列的极限都相等，且\(\lim\limits_{x\to x_0}f(x)=\lim\limits_{n\to\infty}f(x_n)\).

【证明】先证必要性：
由\(\lim\limits_{x\to x_0}f(x)\)存在，设\(\lim\limits_{x\to x_0}f(x)=A\)
即\(\forall\varepsilon>0,\exists\delta>0\)，当\(0<|x-x_0|<\delta\)时，都有\(|f(x)-A|<\varepsilon\)
\(\forall\{x_n\} \subset \stackrel{o}{U}(x_0)\)，\(\lim\limits_{n\to\infty}x_n=x_0\)，
要证明\(\lim\limits_{n\to\infty}f(x_n)=A\)
（分析：只要证\(\forall\varepsilon>0,\exists N\)，当\(n>N\)时，都有\(|f(x_n)-A|<\varepsilon\)）
由\(\lim\limits_{n\to\infty}x_n=x_0\)，对上述\(\delta>0\)，\(\exists N\)，当\(n>N\)时都有\(0<|x_n-x_0|<\delta\)（\(x_n\)在空心邻域中，不等于\(x_0\)）
都有\(|f(x_n)-A|<\varepsilon\)
所以\(\lim\limits_{n\to\infty}f(x_n)=A\)
再证充分性：
有\(\forall\{x_n\} \subset \stackrel{o}{U}(x_0)\)，\(\lim\limits_{n\to\infty}x_n=x_0\)，都有\(\lim\limits_{n\to\infty}f(x_n)\)存在且相等，设\(\lim\limits_{n\to\infty}f(x_n)=A\)
我们要证明\(\lim\limits_{x\to x_0}f(x)=A\)，用反证法：
假设\(f(x)\)当\(x\to x_0\)时不以\(A\)为极限（包含了极限不存在或者极限不等于\(A\)两种情况）
即\(\exists \varepsilon_0 >0\)，对无论多么小的\(\delta>0,\exists x_{\delta}\)，虽然\(0<|x_{\delta}-x_0|<\delta\)
但是\(|f(x_{\delta})-A|\geqslant \varepsilon_{0}\)
取\(\frac{\delta}{2}>0,\exists x_1,0<|x_1-x_0|<\frac{\delta}{2}\)，但是\(|f(x_1)-A|\geqslant \varepsilon_0\)
取\(\frac{\delta}{2^2}>0,\exists x_2,0<|x_2-x_0|<\frac{\delta}{2^2}\)，但是\(|f(x_2)-A|\geqslant \varepsilon_0\)
\(\cdots\)
取\(\frac{\delta}{2^n}>0,\exists x_n,0<|x_n-x_0|<\frac{\delta}{2^n}\)，但是\(|f(x_n)-A|\geqslant \varepsilon_0\)
\(\cdots\)
构造出一个数列\(\{x_n\}\subset \stackrel{o}{U}(x_0)\)且\(0<|x_n-x_0|<\frac{\delta}{2^n}\)

由于\(\lim\limits_{n\to\infty} 0 = 0,\lim\limits_{n\to\infty}\frac{\delta}{2^n}=0\)
由夹逼定理知\(\lim\limits_{n\to\infty}|x_n-x_0|=0\)
由前置知识中的定理可知\(\lim\limits_{n\to\infty}(x_n-x_0)=0\)
由极限的四则运算可知\(\lim\limits_{n\to\infty}(x_n-x_0)=\lim\limits_{n\to\infty}x_n - \lim\limits_{n\to\infty}x_0=(\lim\limits_{n\to\infty}x_n) - x_0=0\)
即\(\lim\limits_{n\to\infty}x_n=x_0\)
（或者按苏老师的思路写成这样也行\(\lim\limits_{n\to\infty}x_n=\lim\limits_{n\to\infty}(x_0+(x_n-x_0))\)）
但是此时的\(|f(x_n)-A|\geqslant \varepsilon_0\)
从而知\(f(x_n)\)当\(n\)趋于无穷大时不是以\(A\)为极限与\(\lim\limits_{n\to\infty}f(x_n)=A\)矛盾
所以假设不成立，故\(\lim\limits_{x\to x_0}f(x)=A\).

海涅定理的推论

【推论】若\(\exists \{x_{n}'\},\{x_{n}''\}\subset \stackrel{o}{U}(x_0)\)且\(\lim\limits_{n\to\infty}x_{n}'=x_0,\lim\limits_{n\to\infty}x_{n}''=x_0\)，有\(\lim\limits_{n\to\infty}f(x_{n}')=B,\lim\limits_{n\to\infty}f(x_{n}'')=B\)，且\(B\ne C\)或者\(\exists \{x_n\}\subset \stackrel{o}{U}(x_0)\)且\(\lim\limits_{n\to\infty}f(x_n)\)不存在，则\(\lim\limits_{x\to x_0}f(x)\)不存在。

【注】给证明数列不存在，排除选择题选项带来了方便。