【自学嵌入式:计算机组成原理】27. 乘法和除法电路的实现原理
27. 乘法和除法电路的实现原理
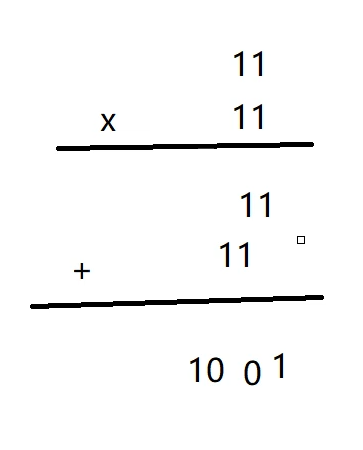
二进制乘法需要有一个与门和一个移位器

计算机的四则运算实现逻辑
计算机的加减乘除运算并非依赖独立电路,而是以加法电路为核心,通过逻辑转换与硬件优化,统一实现所有算术操作。以下从基础原理到硬件设计逐步解析,帮助理解底层逻辑。
一、加减法:共享加法电路
计算机中,加法与减法均通过加法电路完成,核心逻辑是将减法转换为“加上负数的补码”(补码规则:负数的补码 = 正数原码按位取反 + 1 )。
示例:计算 \(5 - 3\)
-
减法转加法:利用补码,减法可表示为加法:
\[5 - 3 = 5 + (-3) \] -
求负数的补码(以8位二进制为例):
- 正数 \(3\) 的原码:\(0000\ 0011\)
- 按位取反:\(1111\ 1100\)
- 加1得到补码:\(1111\ 1101\)(即 \(-3\) 的补码)
-
加法电路运算:
正数 \(5\) 的补码(与原码一致)为 \(0000\ 0011\),与 \(-3\) 的补码 \(1111\ 1101\) 相加:\[0000\ 0011 + 1111\ 1101 = 1\ 0000\ 0000 \]截断8位后结果为 \(0000\ 0010\)(对应十进制 \(2\) )。
因此,加减法共用一套加法电路,减法仅需额外的“补码转换”逻辑。
二、乘法:多次加法与硬件优化
乘法的本质是重复加法,但现代计算机通过二进制移位 + 与门优化,大幅提升运算效率。
1. 基本原理:乘法 = 多次加法
十进制中,乘法可拆解为重复加法。例如:
早期计算机通过“循环加法”实现乘法,但纯软件循环效率极低,需硬件优化。
2. 二进制乘法优化:移位 + 与门
二进制乘法利用“位运算特性”简化:乘数的每一位决定是否将被乘数左移对应位数后累加。
示例:二进制乘法 \(11_2 \times 11_2\)(即十进制 \(3 \times 3\) )
- 被乘数:\(11_2\)(十进制 \(3\) )
- 乘数:\(11_2\)(十进制 \(3\) )
二进制乘法规则:
- 乘数的低位(第0位)为 \(1\) → 加 \(\text{被乘数} \ll 0\)(即 \(11_2\) );
- 乘数的高位(第1位)为 \(1\) → 加 \(\text{被乘数} \ll 1\)(即 \(110_2\) );
- 最终累加:\(11_2 + 110_2 = 1001_2\)(对应十进制 \(9\) )。
硬件实现:与门 + 移位器 + 加法器
- 与门:判断乘数的每一位是否为 \(1\)(若为 \(1\),则触发对应移位操作)。
- 移位器:根据乘数的位位置,将被乘数左移相应位数(如第 \(n\) 位为 \(1\),则左移 \(n\) 位)。
- 加法器:累加所有移位后的结果,得到最终乘积。
三、除法:多次减法
除法的本质是重复减法,核心逻辑是“求商(减法次数)与余数(最终剩余值)”。
示例:计算 \(10 \div 3\)
通过重复减法实现:
- 减法次数:\(3\) 次(商为 \(3\) )
- 最终剩余:\(1\)(余数为 \(1\) )
计算机实现逻辑
计算机中,除法通过“循环减法 + 计数器”实现:
- 初始化商为 \(0\),余数为被除数;
- 当余数 ≥ 除数时,执行 \(\text{余数} = \text{余数} - \text{除数}\),并将商加 \(1\);
- 直到余数 < 除数,停止操作。
四、现代计算机的优化方向
为提升运算效率,现代计算机针对乘除法设计了专用硬件电路:
1. 移位乘法/除法电路
利用二进制“左移(乘法)/右移(除法)”的高效性,替代纯软件循环:
- 乘法:\(a \times 2^n\) 直接通过左移 \(n\) 位实现(无需多次加法)。
- 除法:\(a \div 2^n\) 直接通过右移 \(n\) 位实现(无需多次减法)。
2. 小数运算电路
处理带小数的乘除时(如浮点数),需遵循IEEE 754 标准,通过“符号位、指数位、尾数位”的分离与组合,设计专用电路实现高效运算。
总结
计算机的四则运算以加法电路为基础,通过逻辑转换与硬件优化实现:
- 加减法:减法转补码加法,共享加法电路;
- 乘法:本质是多次加法,通过移位 + 与门优化硬件实现;
- 除法:本质是多次减法,通过循环减法与计数器实现;
- 现代优化:专用移位电路、浮点数运算电路,进一步提升效率。
理解这一逻辑,可掌握计算机算术运算的底层设计思想——用简单电路实现复杂操作,通过逻辑转换与硬件优化平衡功能与效率。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号