【深度学习数学基础：概率论与数理统计】1.1.6 事件间的运算

1. 随机事件与概率

1.1 随机事件及其运算

1.1.6 事件间的运算

事件的运算与集合的运算相当，有并、交、差和余四种运算。

一、事件\(A\)与\(B\)的并

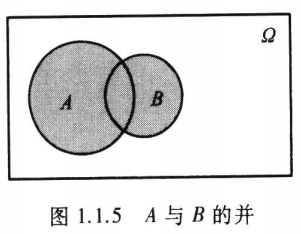
记为\(A \cup B\)。其含义为“由事件\(A\)与\(B\)中所有的样本点（相同的只计入一次）组成的新事件”（见图1.1.5）。或用概率论的语言说“事件\(A\)与\(B\)中至少有一个发生”。

如在掷一颗骰子的试验中，记事件\(A=\)“出现奇数点”\(= \{1, 3, 5\}\)，记事件\(B=\)“出现的点数不超过3”\(= \{1, 2, 3\}\)，则\(A\)与\(B\)的并为\(A \cup B = \{1, 2, 3, 5\}\)。

二、事件\(A\)与\(B\)的交

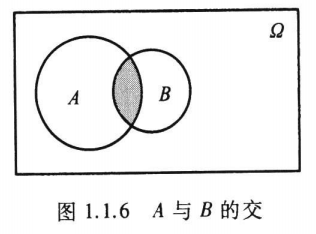
记为\(A \cap B\)，或简记为\(AB\)。其含义为“由事件\(A\)与\(B\)中公共的样本点组成的新事件”（见图1.1.6）。或用概率论的语言说“事件\(A\)与\(B\)同时发生”。

如在掷一颗骰子的试验中，记事件\(A=\)“出现奇数点”\(= \{1, 3, 5\}\)，记事件\(B=\)“出现的点数不超过3”\(= \{1, 2, 3\}\)，则\(A\)与\(B\)的交为\(AB = \{1, 3\}\)。

若事件\(A\)与\(B\)互不相容，则其交必为不可能事件，即\(AB = \varnothing\)，反之亦然。这表明：\(AB = \varnothing\)就意味着\(A\)与\(B\)是互不相容事件。

事件的并与交运算可推广到有限个或可列个事件，譬如有事件\(A_1, A_2, \cdots\)，则\(\bigcup\limits_{i=1}^n A_i\)称为有限并，\(\bigcup\limits_{i=1}^\infty A_i\)称为可列并，\(\bigcap\limits_{i=1}^n A_i\)称为有限交，\(\bigcap\limits_{i=1}^\infty A_i\)称为可列交。

三、事件\(A\)对\(B\)的差

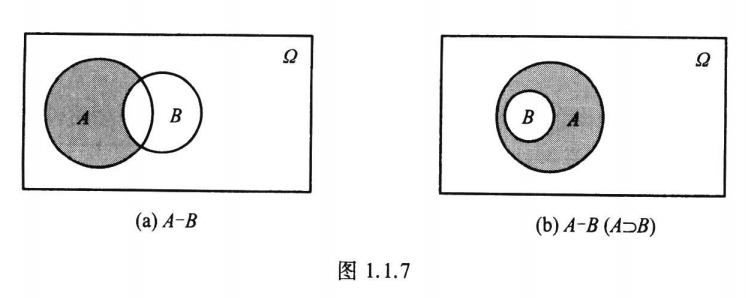
记为\(A - B\)。其含义为“由在事件\(A\)中而不在\(B\)中的样本点组成的新事件”（见图1.1.7）。或用概率论的语言说“事件\(A\)发生而\(B\)不发生”。

如在掷一颗骰子的试验中，记事件\(A=\)“出现奇数点”\(= \{1, 3, 5\}\)，记事件\(B=\)“出现的点数不超过3”\(= \{1, 2, 3\}\)，则\(A\)对\(B\)的差为\(A - B = \{5\}\)。

若设\(X\)为随机变量，则有：

\[\{X = a\} = \{X \leqslant a\} - \{X < a\}, \quad \{a < X \leqslant b\} = \{X \leqslant b\} - \{X \leqslant a\}. \]

四、对立事件

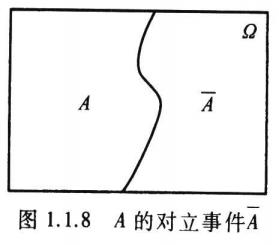
事件\(A\)的对立事件，记为\(\bar{A}\)，即“由在\(\Omega\)中而不在\(A\)中的样本点组成的新事件”（见图1.1.8），或用概率论的语言说“\(A\)不发生”，即\(\bar{A} = \Omega - A\)。注意，对立事件是相互的，即\(A\)的对立事件是\(\bar{A}\)，而\(\bar{A}\)的对立事件是\(A\)，即\(\overline{\bar{A}} = A\)。必然事件\(\Omega\)与不可能事件\(\varnothing\)互为对立事件，即\(\bar{\Omega} = \varnothing\)，\(\bar{\varnothing} = \Omega\)。

如在掷一颗骰子的试验中，事件\(A=\)“出现奇数点”\(= \{1, 3, 5\}\)的对立事件是\(\bar{A} = \{2, 4, 6\}\)，事件\(B=\)“出现的点数不超过3”\(= \{1, 2, 3\}\)的对立事件是\(\bar{B} = \{4, 5, 6\}\)。

\(A\)与\(B\)互为对立事件的充要条件是：\(A \cap B = \varnothing\)，且\(A \cup B = \Omega\)。

此性质也可作为对立事件的另一种定义，即如果事件\(A\)与\(B\)满足：\(A \cap B = \varnothing\)，且\(A \cup B = \Omega\)，则称\(A\)与\(B\)互为对立事件，记为\(\bar{A} = B\)，\(\bar{B} = A\)。

需要注意的是：
（1）对立事件一定是互不相容的事件，即\(A \cap \bar{A} = \varnothing\)。但互不相容的事件不一定是对立事件，比如下图中\(A\)与\(B\)互不相容，但却不是对立事件：

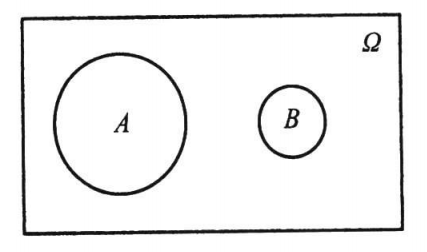
（2）\(A - B\)可以记为\(A\bar{B}\)。

例1.1.8 从数字\(1, 2, \cdots, 9\)中可重复地任取\(n\)次（\(n \geqslant 2\)），以\(A\)表示事件“所取的\(n\)个数字的乘积能被10整除”。因为乘积能被10整除必须既取到数字5，又要取到偶数，所以\(A\)的对立事件\(\bar{A}\)为“所取的\(n\)个数字中或者没有5，或者没有偶数”。如果记\(B=\)“所取的\(n\)个数字中没有5”，\(C=\)“所取的\(n\)个数字中没有偶数”，则\(\bar{A} = B \cup C\)。

例1.1.9 设\(A, B, C\)是某个随机现象的三个事件，则：
（1）事件“\(A\)与\(B\)发生，\(C\)不发生”可表示为：\(AB\bar{C} = AB - C\)。
（2）事件“\(A, B, C\)中至少有一个发生”可表示为：\(A \cup B \cup C\)。
（3）事件“\(A, B, C\)中至少有两个发生”可表示为：\(AB \cup AC \cup BC\)。
（4）事件“\(A, B, C\)中恰好有两个发生”可表示为：\(AB\bar{C} \cup A\bar{B}C \cup \bar{A}BC\)。
（5）事件“\(A, B, C\)同时发生”可表示为：\(ABC\)。
（6）事件“\(A, B, C\)都不发生”可表示为：\(\bar{A}\bar{B}\bar{C}\)。
（7）事件“\(A, B, C\)不全发生”可表示为：\(\bar{A} \cup \bar{B} \cup \bar{C}\)。

五、事件的运算性质

【补】吸收律：
\(A \cup (A \cap B) = A\)
\(A \cap (A \cup B) = A\)

1. 交换律
   \(A \cup B = B \cup A\)，\(AB = BA\)．\((1.1.1)\)

2. 结合律
   \((A \cup B) \cup C = A \cup (B \cup C)\)，\((1.1.2)\)
   \((AB)C = A(BC)\)．\((1.1.3)\)

3. 分配律
   \((A \cup B) \cap C = AC \cup BC\)，\((1.1.4)\)
   \((A \cap B) \cup C = (A \cup C) \cap (B \cup C)\)．\((1.1.5)\)

4. 对偶律（德摩根公式）
   事件并的对立等于对立的交：\(\overline{A \cup B} = \overline{A} \cap \overline{B}\)，\((1.1.6)\)
   事件交的对立等于对立的并：\(\overline{A \cap B} = \overline{A} \cup \overline{B}\)．\((1.1.7)\)

事件运算的对偶律是很有用的公式．这些性质是不难证明的，在此我们用集合论的语言证明其中的\((1.1.6)\)式．

\((1.1.6)\)式的证明

设\(\omega \in \overline{A \cup B}\)，即\(\omega \notin A \cup B\)，这表明\(\omega\)既不属于\(A\)，也不属于\(B\)，这意味着\(\omega \notin A\)和\(\omega \notin B\)同时成立，所以\(\omega \in \overline{A}\)与\(\omega \in \overline{B}\)同时成立，于是有\(\omega \in \overline{A} \cap \overline{B}\)，这说明：

\[\overline{A \cup B} \subset \overline{A} \cap \overline{B}. \]

反之，设\(\omega \in \overline{A} \cap \overline{B}\)，即同时有\(\omega \in \overline{A}\)和\(\omega \in \overline{B}\)，从而同时有\(\omega \notin A\)和\(\omega \notin B\)，这意味着\(\omega\)不属于\(A\)与\(B\)中的任一个，即\(\omega \notin A \cup B\)，也就是有\(\omega \in \overline{A \cup B}\)，这说明：

\[\overline{A \cup B} \supset \overline{A} \cap \overline{B}. \]

综合上述两方面，可得：

\[\overline{A \cup B} = \overline{A} \cap \overline{B}. \]

\((1.1.6)\)式得证．

德摩根公式可推广到多个事件及可列个事件场合：

\[\overline{\bigcup\limits_{i=1}^n A_i} = \bigcap\limits_{i=1}^n \overline{A_i}, \quad \overline{\bigcup\limits_{i=1}^\infty A_i} = \bigcap\limits_{i=1}^\infty \overline{A_i}, \quad (1.1.8) \]

\[\overline{\bigcap\limits_{i=1}^n A_i} = \bigcup\limits_{i=1}^n \overline{A_i}, \quad \overline{\bigcap\limits_{i=1}^\infty A_i} = \bigcup\limits_{i=1}^\infty \overline{A_i}. \quad (1.1.9) \]