【深度学习数学基础：高等数学】【苏德矿高等数学】第9讲：子数列推论、函数极限定义

2. 数列极限

2.2 数列极限

2.2.10 子数列推论

子数列推论

【推论】若\(\{a_n\}\)中挑选出两个子数列极限存在但不相等或挑选出一个子数列极限不存在，则\(\{a_n\}\)发散。

【例】证明\(\{\sin \frac{n\pi}{4}\}\)发散。
【证明】取\(n=8k,k\in\mathbb{N}\)，\(\{\sin\frac{8k\pi}{4}\}=\{\sin 2k\pi\}=\{0\}\)极限为\(0\)
取\(n=8k+2,k\in\mathbb{N}\)，\(\{\sin\frac{(8k+2)\pi}{4}\}=\{\sin(2k\pi+\frac{\pi}{2})\}=\{1\}\)极限为\(1\)
由\(0\ne 1\)知\(\{\sin \frac{n\pi}{4}\}\)发散。

【例】证明\(\{(-1)^{n-1}\}\)发散。
【证明】取\(n=2k,k\in\mathbb{N}\)，\(\{(-1)^{2k-1}\}=\{-1\}\)极限为\(-1\)
取\(n=2k-1,k\in\mathbb{N}\)（如果取\(n=2k+1\)，则\(k=0,1,2,\cdots\)，因为数列项数从1开始）\(\{(-1)^{2k-2}\}=\{1\}\)极限为\(1\)
由\(-1\ne 1\)知\(\{(-1)^{n-1}\}\)发散。

奇偶子数列收敛且相等，原数列收敛

【定理】\(\{a_n\}\)收敛的充要条件是\(\{a_{2k}\},\{a_{2k-1}\}\)极限都存在并且相等。
【证明】先证必要性：
由于\(\{a_n\}\)收敛，设\(\lim\limits_{n\to\infty}a_n=a\)，\(\forall\varepsilon>0,\exists N_1\)，
当\(x>N\)时，都有\(|a_n-a|<\varepsilon\)
取\(N_2=\frac{N_1}{2}\)，当\(k>N_2\)即\(2k>2N_2=N_1\)时，都有\(|a_{2k}-a|<\varepsilon\)
则\(\lim\limits_{n\to\infty}a_{2k}=a\)
取\(N_3=\frac{N_1 + 1}{2}\)，当\(k>N_3\)即\(2k-1>2N_3-1=N_1+1-1=N_1\)时，都有\(|a_{2k-1}-a|<\varepsilon\)
则\(\lim\limits_{n\to\infty}a_{2k-1}=a\)
再证充分性：
设\(\lim\limits_{n\to\infty}a_{2k}=\lim\limits_{n\to\infty}a_{2k-1}=a\)
\(\forall\varepsilon>0,\exists N_1\)，当\(k>N_1\)时，都有\(|a_{2k}-a|<\varepsilon\)
\(\exists N_2\)，当\(k>N_2\)时，都有\(|a_{2k-1}-a|<\varepsilon\)
令\(N=\max\{2N_1,2N_2-1\}\)，当\(n>N\)时都有\(|a_n-a|<\varepsilon\)
则\(\lim\limits_{n\to\infty}a_n=a\)

3. 函数极限

3.1 函数极限的概念

3.1.1 函数极限定义

背景引入

我们说，其实数列就是特殊的函数，\(y=f(n),n\in\mathbb{N}\)
【例】\(f(n)=\frac{1}{n},n\in\mathbb{N}\)，\(f(n):1,\frac{1}{2},\frac{1}{3},\cdots,\frac{1}{n},\cdots\)，下面给出其图像：

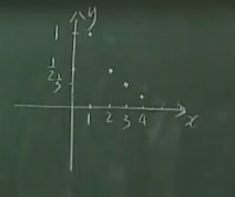
所以说数列的图像是屏幕上离散的点
\(\lim\limits_{n\to\infty}\frac{1}{n}=0\).

【例】\(f(x)=\frac{1}{x},x>0\)

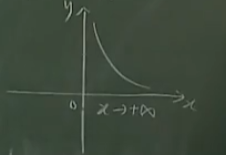
当\(x\to +\infty\)，曲线与\(x\)轴无限接近，也就是\(\lim\limits_{x\to +\infty}\frac{1}{x}=0\).

给出\(\lim\limits_{n\to \infty}f(n)=A\)：\(\forall\varepsilon>0,\exists N\)，当\(n>N\)时，都有\(|f(n)-A|<\varepsilon\).

可模仿给出函数极限\(\lim\limits_{x\to +\infty}f(x)=A\)的定义。

一般定义

【定义】设\(f(x)\)在\([a,+\infty)\)上有定义（\(a\)是某个常数），\(A\)是一个确定的常数，若\(\forall\varepsilon>0,\exists X>0\)（总能找到一个正数，但是\(X\)若是负数，假如\(x>0.5\)，那更能说明此定义成立），当\(x>X\)（的一切实数）时，都有\(|f(x)-A|<\varepsilon\)，称\(f(x)\)当\(x\)趋于\(+\infty\)时的极限为\(A\)，记作\(\lim\limits_{x\to +\infty}f(x)=A\)或\(f(x)\to A(x\to +\infty)\). （也是找到一个界限\(X\)，但是为了以后统一说明，要求\(X>0\)）


【定义】设\(f(x)\)在\((-\infty,a]\)上有定义（\(a\)是某个常数），\(A\)是一个确定的常数，若\(\forall\varepsilon>0,\exists X>0\)，当\(x<-X\)时，都有\(|f(x)-A|<\varepsilon\)，称\(f(x)\)当\(x\)趋于\(-\infty\)时的极限为\(A\)，记作\(\lim\limits_{x\to -\infty}f(x)=A\)或\(f(x)\to A(x\to -\infty)\).


【定义】【\(\infty\)既包含\(+\infty\)，又包含\(-\infty\)】设\(f(x)\)在\((-\infty,a]\cup [b,+\infty]\)（\(a\leqslant b\)均为常数），\(A\)是一个确定的常数，若\(\forall\varepsilon>0,\exists X>0\)，当\(|x|>X\)时（\(x<-X\)或\(x>X\)），都有\(|f(x)-A|<\varepsilon\)，称\(f(x)\)当\(x\)趋于\(\infty\)时的极限为\(A\)，记作\(\lim\limits_{x\to \infty}f(x)=A\)或\(f(x)\to A(x\to \infty)\).