【自学嵌入式：计算机组成原理】21. 全加器电路的搭建

21. 全加器电路的搭建

全加器（Full Adder）

全加器是数字电路中实现多位数二进制加法的核心组件，相比半加器（仅处理两个1位二进制数，无进位输入），全加器支持接收低位进位信号，可完整处理“加数 + 加数 + 低位进位”的运算，是构建多位加法器的基础。

一、核心定义与组成

（1）功能特点

全加器接收 3个输入：

• 两个1位二进制加数 \(A\)、\(B\)；
• 低位传递的进位信号 \(C_{\text{in}}\)（来自更右侧低位的加法进位）。

输出 2个结果：

• 本位和 \(\text{Sum}\)（1位二进制）；
• 新的进位信号 \(C_{\text{out}}\)（传递给更左侧高位的进位）。

（2）电路组成

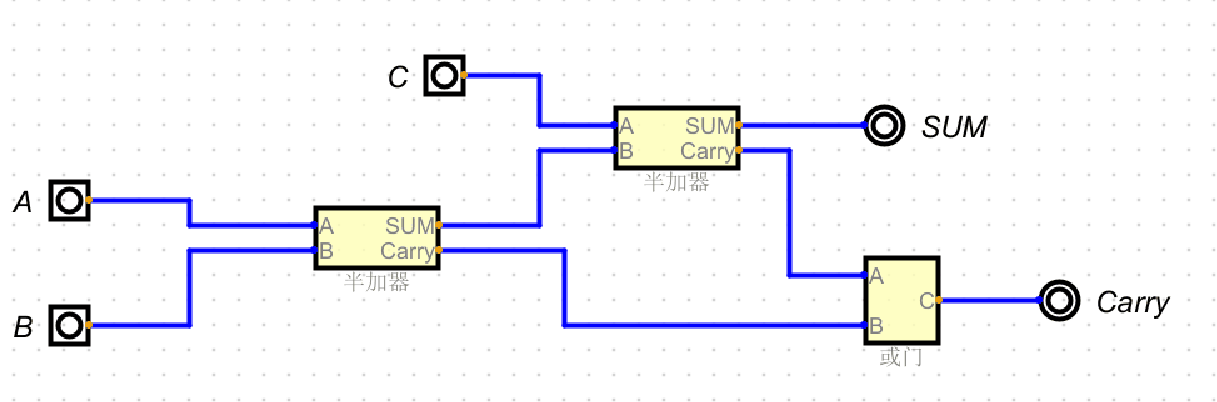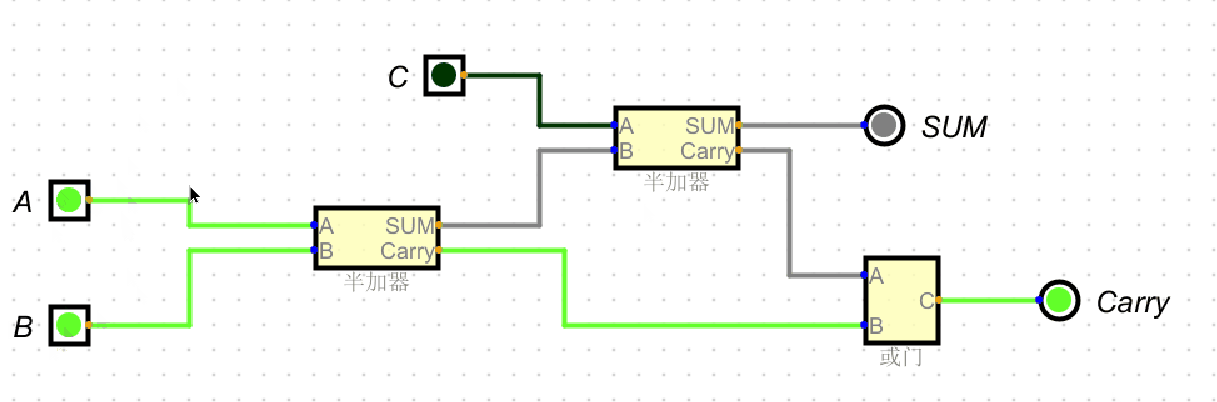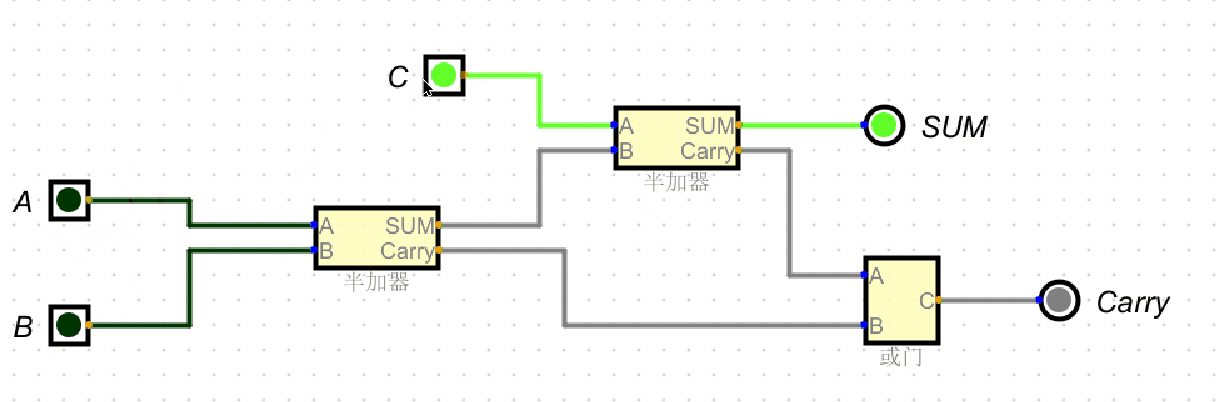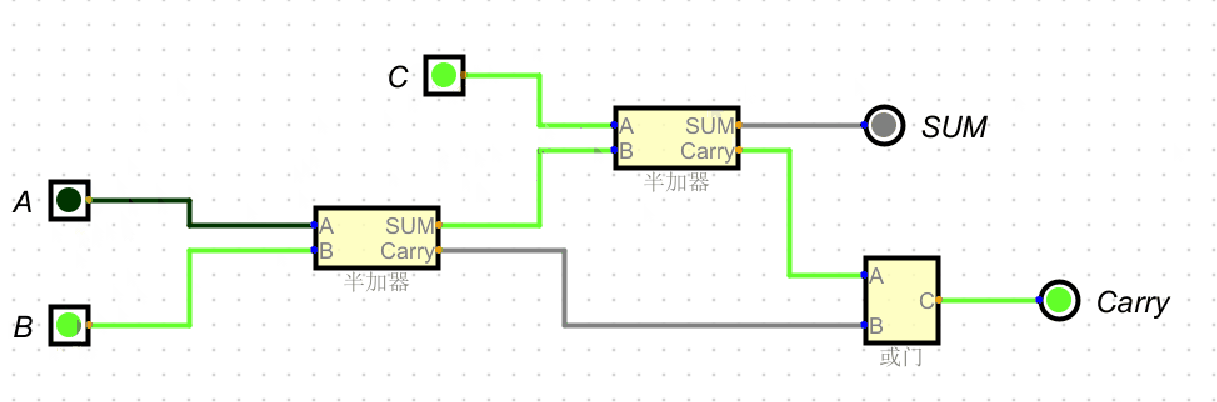
全加器由 两个半加器 + 一个或门 组合实现，结构与信号流程如下：

1. 第一个半加器：处理加数 \(A\) 和 \(B\)，输出中间和 \(A \oplus B\) 与中间进位 \(A \land B\)；
2. 第二个半加器：处理“中间和”与低位进位 \(C_{\text{in}}\)，输出最终和 \(\text{Sum} = (A \oplus B) \oplus C_{\text{in}}\)；
3. 或门：合并“中间进位”与“第二个半加器的进位”，输出最终进位 \(C_{\text{out}} = (A \land B) \lor \left[(A \oplus B) \land C_{\text{in}}\right]\)。

二、真值表（输入-输出映射）

全加器有 \(2^3 = 8\) 种输入组合，真值表完整枚举所有情况：

输入 \(A\)	输入 \(B\)	低位进位 \(C_{\text{in}}\)	本位和 \(\text{Sum}\)	高位进位 \(C_{\text{out}}\)	二进制加法示例（含进位）
\(0\)	\(0\)	\(0\)	\(0\)	\(0\)	\(0 + 0 + 0 = 0\)（进位 \(0\)）
\(0\)	\(0\)	\(1\)	\(1\)	\(0\)	\(0 + 0 + 1 = 1\)（进位 \(0\)）
\(0\)	\(1\)	\(0\)	\(1\)	\(0\)	\(0 + 1 + 0 = 1\)（进位 \(0\)）
\(0\)	\(1\)	\(1\)	\(0\)	\(1\)	\(0 + 1 + 1 = 10_2\)（进位 \(1\)）
\(1\)	\(0\)	\(0\)	\(1\)	\(0\)	\(1 + 0 + 0 = 1\)（进位 \(0\)）
\(1\)	\(0\)	\(1\)	\(0\)	\(1\)	\(1 + 0 + 1 = 10_2\)（进位 \(1\)）
\(1\)	\(1\)	\(0\)	\(0\)	\(1\)	\(1 + 1 + 0 = 10_2\)（进位 \(1\)）
\(1\)	\(1\)	\(1\)	\(1\)	\(1\)	\(1 + 1 + 1 = 11_2\)（进位 \(1\)）

三、工作原理与示例

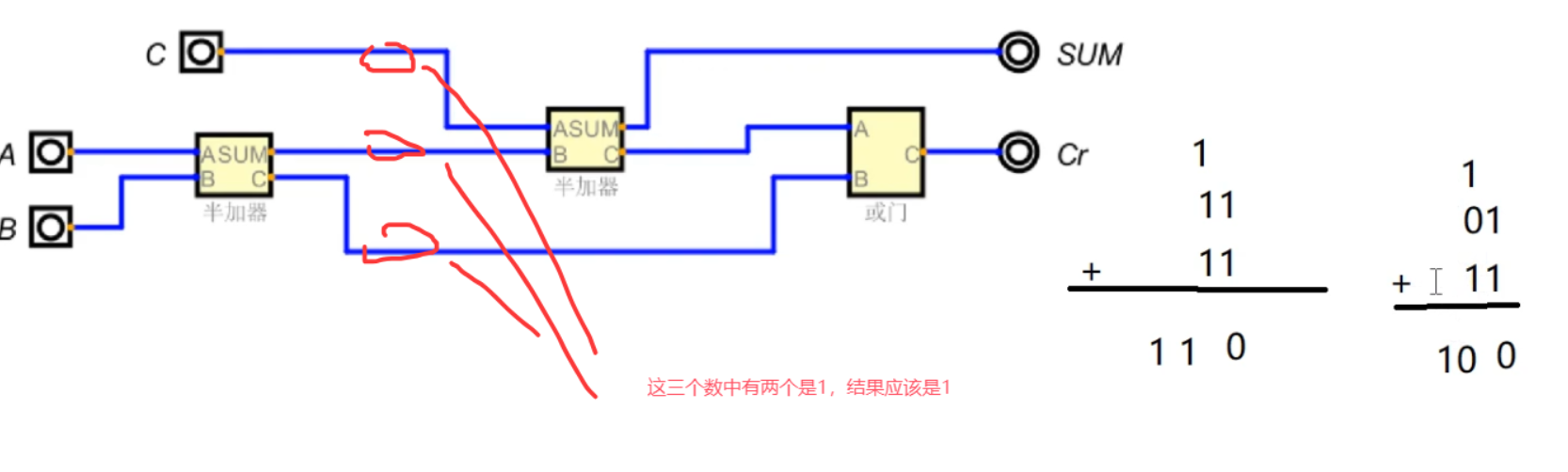
以二进制加法 \(11_2 + 11_2\)（即十进制 \(3 + 3\)）为例，展示全加器如何处理多位进位：

（1）个位加法（最右侧位）

输入：\(A=1\)、\(B=1\)、\(C_{\text{in}}=0\)（无低位进位）。

• 第一个半加器：\(1 \oplus 1 = 0\)（中间和），\(1 \land 1 = 1\)（中间进位）；
• 第二个半加器：\(0 \oplus 0 = 0\)（本位和 \(\text{Sum}=0\)）；
• 或门：\(1 \lor (0 \land 0) = 1\)（高位进位 \(C_{\text{out}}=1\)）。
  结果：个位和为 \(0\)，向十位进 \(1\)。

（2）十位加法（中间位）

输入：\(A=1\)、\(B=1\)、\(C_{\text{in}}=1\)（来自个位的进位）。

• 第一个半加器：\(1 \oplus 1 = 0\)（中间和），\(1 \land 1 = 1\)（中间进位）；
• 第二个半加器：\(0 \oplus 1 = 1\)（本位和 \(\text{Sum}=1\)）；
• 或门：\(1 \lor (0 \land 1) = 1\)（高位进位 \(C_{\text{out}}=1\)）。
  结果：十位和为 \(1\)，向百位进 \(1\)。

（3）最终结果

合并各位和与进位，\(11_2 + 11_2 = 110_2\)（即十进制 \(6\)），与全加器真值表一致。

四、核心意义

全加器通过整合低位进位，解决了半加器无法处理多位数连续加法的缺陷。多个全加器级联（每一位对应一个全加器）可构建多位加法器（如8位、32位加法器），是CPU中算术逻辑单元（ALU）实现加法运算的基础。

总结：
全加器通过“两个半加器 + 或门”的组合，支持“加数 + 加数 + 低位进位”的完整运算，其真值表与电路设计体现了“进位传递”的核心逻辑，是构建复杂算术运算单元的基石。