【自学嵌入式：计算机组成原理】14. 或门电路的搭建

14. 或门电路的搭建

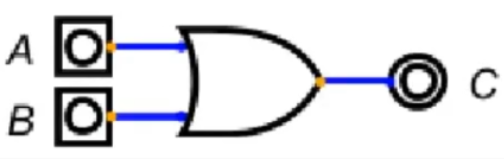
或门是数字电路中实现“逻辑或”运算的基础组件，核心规则为：只要任意一个输入为 1（真/有信号），输出即为 1；仅当所有输入为 0（假/无信号）时，输出为 0。

一、或门的输入输出规则（真值表）

或门通常包含 2个输入（记为 \(A\)、\(B\)）和 1个输出（记为 \(C\)）。其逻辑关系可通过真值表（枚举所有输入组合的输出结果）完整描述：

输入 \(A\)	输入 \(B\)	输出 \(C\)	布尔表达式（或运算）
\(0\)	\(0\)	\(0\)	\(0 \lor 0 = 0\)（或 \(0 + 0 = 0\)）
\(0\)	\(1\)	\(1\)	\(0 \lor 1 = 1\)（或 \(0 + 1 = 1\)）
\(1\)	\(0\)	\(1\)	\(1 \lor 0 = 1\)（或 \(1 + 0 = 1\)）
\(1\)	\(1\)	\(1\)	\(1 \lor 1 = 1\)（或 \(1 + 1 = 1\)）

二、或门的电路模型（并联开关类比）

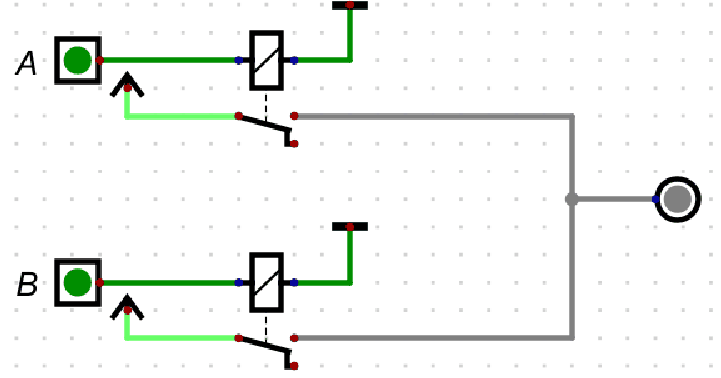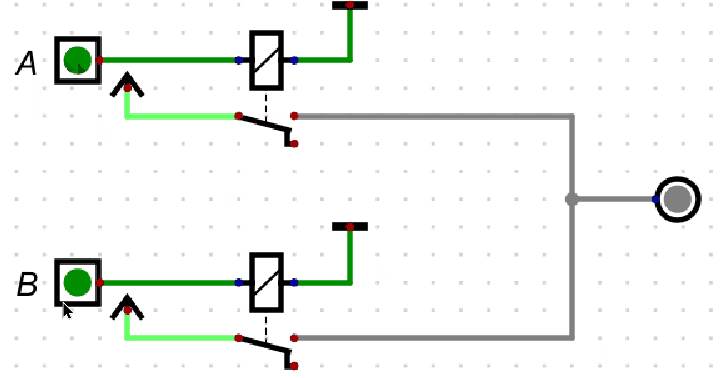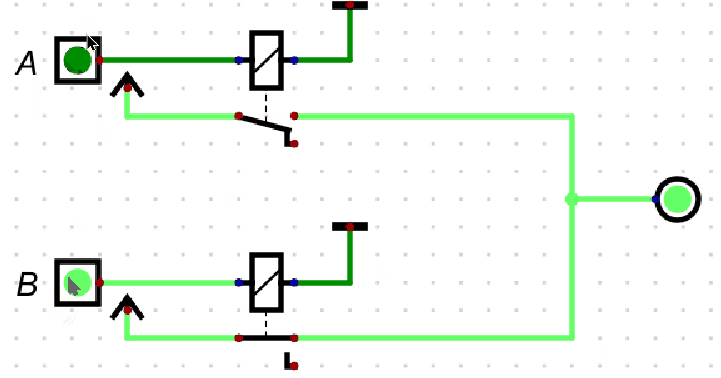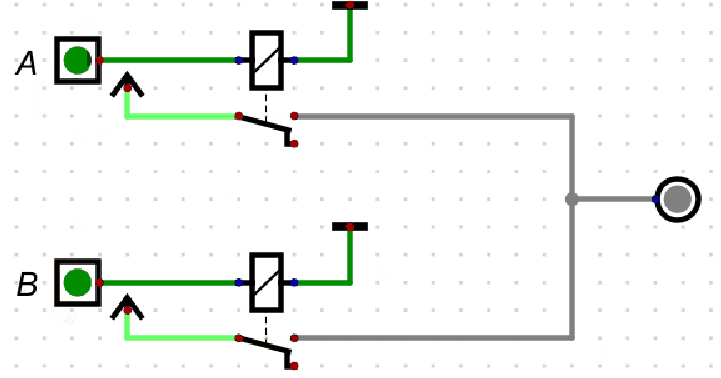
或门的逻辑可通过两个并联的开关直观理解：

• 输入 \(A\) 和 \(B\) 对应两个并联的开关，任意一个开关闭合（输入为 1）即可使电路导通（输出 \(C=1\)）；
• 仅当所有开关断开（输入均为 0）时，电路断开（输出 \(C=0\)）。

三、现实场景示例（条件满足其一即可）

假设：

• 输入 \(A\) 表示“下雨”（1=下雨，0=不下雨）；
• 输入 \(B\) 表示“下雪”（1=下雪，0=不下雪）；
• 输出 \(C\) 表示“是否不去学校”（1=不去，0=去）。

则：

• 若下雨（\(A=1\)）或下雪（\(B=1\)）→ \(C=1\)（不去学校，对应 \(1 \lor 0 = 1\) 或 \(0 \lor 1 = 1\)）；
• 若既不下雨也不下雪（\(A=0, B=0\)）→ \(C=0\)（正常去学校，对应 \(0 \lor 0 = 0\)）。

四、或门的符号与本质

在数字电路中，或门的简化符号为“开口朝左的半圆箭头”（见课程图示）。其本质是通过并联逻辑，将“满足任意条件”的现实需求映射为二进制运算，是构建复杂逻辑判断（如多路选择、故障检测）的基础单元。

总结：
或门通过“任意输入为 1 则输出 1”的规则，实现逻辑或运算。其布尔表达式 \(C = A \lor B\)（或 \(C = A + B\)）与真值表、电路模型一一对应，是理解“条件满足其一即触发结果”类逻辑的核心工具。