【自学嵌入式：计算机组成原理】11. 声音的二进制存储

11. 声音的二进制存储

声音的数字化需通过采样（Sampling） 和 量化（Quantization） 两个核心步骤，将连续的模拟声音信号转换为离散的二进制数据。

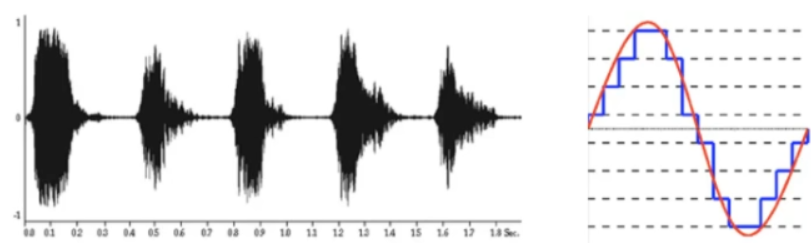
一、采样：时间维度的离散化

（一）核心原理

声音是空气振动产生的连续波信号（模拟信号）。采样是指：以固定时间间隔截取声音信号的振幅值，将连续信号转换为离散的“时间点-振幅”数据对。

（二）关键参数：采样率（Sampling Rate）

采样率定义为单位时间内的采样次数，单位为赫兹（Hz）。例如：

• 44.1kHz（CD音质）：每秒采样 44100 次；
• 48kHz（专业音频）：每秒采样 48000 次。

采样率越高，截取的“时间点”越密集，数字信号对原始声音的还原度越高，但同时数据量也越大（存储需求与采样率正相关）。

二、量化：振幅维度的离散化

（一）核心原理

采样得到的振幅值是连续的模拟量，需进一步转换为离散的数字量（二进制编码）。量化是指：将连续振幅值映射到有限个离散数值，用二进制表示这些数值。

（二）关键参数：量化精度（Bit Depth）

量化精度用二进制位数表示，定义可区分的振幅层级数量。例如：

• 16位精度：可表示 \(2^{16} = 65536\) 个离散振幅值；
• 24位精度：可表示 \(2^{24} = 16777216\) 个离散振幅值。

量化精度越高，振幅的表示越精细（声音细节更丰富），但数据量也越大（存储需求与量化位数正相关）。

三、数字化声音的二进制表示

（一）数据量计算

声音的二进制数据量由采样率、量化精度、声道数共同决定。公式为：

\[\text{数据量（字节/秒）} = \frac{\text{采样率} \times \text{量化位数} \times \text{声道数}}{8} \]

示例（CD音质：44.1kHz采样率、16位精度、立体声2声道）：

\[\text{数据量} = \frac{44100 \times 16 \times 2}{8} = 176400 \text{ 字节/秒} \approx 172 \text{ KB/s} \]

（二）存储与还原

二进制数据存储为音频文件（如WAV、MP3）后，播放时通过数模转换（DAC） 还原：

1. 读取二进制数据，解析为采样率、量化精度、振幅序列；
2. 按采样率重建连续波形，驱动扬声器振动发声。

总结：
声音的二进制表示依赖“采样（时间离散化）+ 量化（振幅离散化）”。采样率与量化精度决定声音还原度，同时直接影响存储数据量。理解这两个步骤，是掌握音频数字化、压缩编码（如MP3）的基础。