【深度学习数学基础：概率论与数理统计】1.1.5 事件间的关系

1. 随机事件与概率

1.1 随机事件及其运算

1.1.5 事件间的关系

下面的讨论总是假设在同一个 样本空间\(\boldsymbol{\Omega}\)（即同一个随机现象）中进行。事件间的关系与集合间的关系一样，主要有以下几种：

一、包含关系

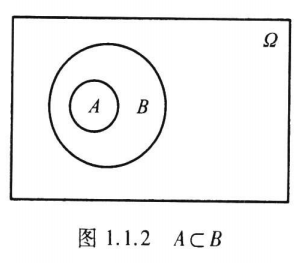
如果属于\(A\)的样本点必属于\(B\)，则称\(A\)被包含在\(B\)中（见图1.1.2），或称\(B\)包含\(A\)，记为\(\boldsymbol{A \subset B}\)，或\(\boldsymbol{B \supset A}\)。用概率论的语言说：事件\(A\)发生必然导致事件\(B\)发生。

譬如掷一颗骰子，事件\(A=\)“出现4点”的发生必然导致事件\(B=\)“出现偶数点”的发生，故\(A \subset B\)。

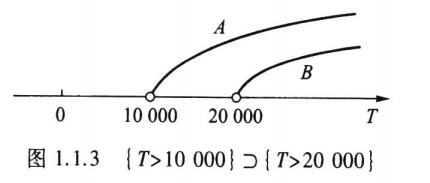
又如电视机的寿命\(T\)超过\(10000\ \text{h}\)（记为事件\(\boldsymbol{A = \{ T > 10000 \}}\)）和\(T\)超过\(20000\ \text{h}\)（记为事件\(\boldsymbol{B = \{ T > 20000 \}}\)），则\(A \supset B\)，见图1.1.3。

对任一事件\(A\)，必有\(\boldsymbol{\varnothing \subset A \subset \Omega}\)。

二、相等关系

如果事件\(A\)与事件\(B\)满足：属于\(A\)的样本点必属于\(B\)，而且属于\(B\)的样本点必属于\(A\)，即\(\boldsymbol{A \subset B}\)且\(\boldsymbol{B \subset A}\)，则称事件\(A\)与\(B\)相等，记为\(\boldsymbol{A = B}\)。

从集合论观点看，两个事件相等就意味着这两事件是同一个集合。下例说明：有时不同语言描述的事件也可能是同一事件。

例1.1.6 掷两颗骰子，以\(A\)记事件“两颗骰子的点数之和为奇数”，以\(B\)记事件“两颗骰子的点数为一奇一偶”。很容易证明：\(A\)发生必然导致\(B\)发生，而且\(B\)发生也必然导致\(A\)发生，所以\(A = B\)。

例1.1.7 口袋中有\(a\)个黑球，\(b\)个白球（\(a\)与\(b\)都大于零），从中不返回地一个一个摸球，直到摸完为止。以\(A\)记事件“最后摸出的几个球全是黑球”，以\(B\)记事件“最后摸出的一个球是黑球”。对于此题粗看好像是\(A \neq B\)，但只要设想将球全部摸完为止，则明显有：\(A\)发生必然导致\(B\)发生，即\(A \subset B\)；反之注意到事件\(A\)中所述的“几个”最少是\(1\)个，也可以是\(2\)个，…，最多为\(a\)个，则\(B\)发生时\(A\)也必然发生（对于这点请读者仔细体会），即\(B \subset A\)，由此得\(A = B\)。

三、互不相容

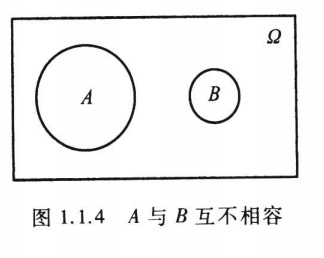
如果\(A\)与\(B\)没有相同的样本点（见图1.1.4），则称\(A\)与\(B\)互不相容。用概率论的语言说：\(A\)与\(B\)互不相容就是事件\(A\)与事件\(B\)不可能同时发生。

如在电视机寿命试验中，“寿命小于\(1\)万小时”与“寿命大于\(5\)万小时”是两个互不相容的事件，因为它们不可能同时发生。