【深度学习数学基础：高等数学】【苏德矿高等数学】第5讲：收敛数列的性质

2. 数列极限

2.2 数列极限

2.2.5 收敛数列的性质

性质1：唯一性

若数列\(\{a_n\}\)有极限，则极限必唯一。
【证法1】用反证法，假设\(\lim\limits_{n\to\infty}a_n=a,\lim\limits_{n\to\infty}a_n=b\)且\(a\ne b\)
对\(\forall\varepsilon>0,\exists N_1\)，当\(n>N_1\)时，都有\(|a_n-a|<\varepsilon\)
对\(\forall\varepsilon>0,\exists N_2\)，当\(n>N_2\)时，都有\(|a_n-b|<\varepsilon\)
取\(N=\max\{N_1,N_2\}\)，当\(n>N\)时，都有\(|a_n-a|<\varepsilon,|a_n-b|<\varepsilon\)
于是\(|a-b|=|a-a_n+a_n-b|\leqslant|a-a_n|+|a_n-b|<\varepsilon+\varepsilon=2\varepsilon\)
则\(a=b\)，矛盾
所以若数列\(\{a_n\}\)有极限，则极限必唯一。
【证法2】用反证法，取\(\varepsilon=\frac{|a-b|}{2}>0\)，
\(\exists N_1\)，当\(n>N_1\)时，都有\(|a_n-a|<\frac{|a-b|}{2}\)
\(\exists N_2\)，当\(n>N_2\)时，都有\(|a_n-b|<\frac{|a-b|}{2}\)
取\(N=\max\{N_1,N_2\}\)，当\(n>N\)时，\(|a-b|=|a-a_n+a_n-b|\leqslant|a-a_n|+|a_n-b|<\frac{|a-b|}{2}+\frac{|a-b|}{2}=|a-b|\)
矛盾（一个数小于本身）
所以若数列\(\{a_n\}\)有极限，则极限必唯一。

收敛

若数列\(\{a_n\}\)有极限，称\(\{a_n\}\)收敛，否则称\(\{a_n\}\)发散。

改变数列有限项不改变数列的收敛性

一个数列改变它的有限项（比如：\(a_1\)换成其他的数），或者在前面去掉数列有限项，或者在前面添加有限项，不改变数列的收敛性。
（因为数列收敛与否和\(n>N\)后的无限项相关。）
即若原来数列收敛，改变后极限值不变。

数列有界

若\(\exists\)常数\(M>0,\forall n\in \mathbb{N}\)，都有\(|a_n|\leqslant M\)，称\(\{a_n\}\)有界。

性质2：收敛的必要条件（有界的充分条件）

若数列\(\{a_n\}\)收敛，则\(\{a_n\}\)有界。
【证明】由数列\(\{a_n\}\)收敛，设\(\lim\limits{n\to\infty}a_n=a\)

假设取\(\varepsilon=1\)，那么邻域外面是有限项，邻域内部是无限项

取\(\varepsilon=1>0\)，由\(\lim\limits_{n\to\infty}a_n=a\)，
\(\exists\)自然数\(N_0\)，当\(n>N_0\)时，都有\(|a_n-a|<1\)
\(|a_n|-|a|\leqslant|a_n-a|<1 \Rightarrow |a_n|<1+|a|\)
记\(M=\max\{|a_1|,|a_2|,\cdots,|a_{N_0}|,1+|a|\}\) （有限项和无限项的界的最大值）
\(\forall n\in \mathbb{N}\)，都有\(|a_n|\leqslant M\)
从而得证。
【错解】设\(\max\{|a_1|,|a_2|,\cdots,|a_{n}|,\cdots\}=M\)，\(\forall n \in \mathbb{N}\)，都有\(|a_n|\leqslant M\)
【错因】有限个数有最大值，无限个数不一定有最大值，反例：\(\max\{1,2,3,\cdots,n\}\)无最大值，正无穷不是它的最大值，正无穷不是一个数，我们要找常数。
【注意】此性质逆命题不成立，反例：\(\{(-1)^n\}\)有界，但\(\{(-1)^n\}\)在后面可以证明它是发散的。

性质3：不等式性质

若\(\lim\limits_{n\to\infty}a_n=a,\lim\limits_{n\to\infty}b_n=b\)，\(a,b\)为常数且\(a<b\)，则\(\exists N_0\)，当\(n>N_0\)时，都有\(a_n<b_n\).

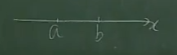
取\(b-a\)长度一半，就可以保证\(b_n\)的邻域落在\(a_n\)的邻域右侧
【证明】取\(\varepsilon=\frac{b-a}{2}>0\)，
\(\exists N_1\)，当\(n>N_1\)时，都有\(|a_n-a|<\frac{b-a}{2}\)
\(\Leftrightarrow a-\frac{b-a}{2}<a_n<a+\frac{b-a}{2}\)
\(\Leftrightarrow \frac{3a-b}{2}<a_n<\frac{a+b}{2}...(1)\)
\(\exists N_2\)，当\(n>N_2\)时，都有\(|b_n-b|<\frac{b-a}{2}\)
\(\Leftrightarrow b-\frac{b-a}{2}<b_n<b+\frac{b-a}{2}\)
\(\Leftrightarrow \frac{a+b}{2}<b_n<\frac{3b-a}{2}...(2)\)
取\(N_0=\max\{N_1,N_2\}\)，当\(n>N_0\)时，都有\(a_n<\frac{a+b}{2}<b_n\)
【推论】\(\exists N_0,n,m>N_0,a_n<b_m\)，下标可以不一致。

性质4：不等式性质

若\(\exists N_0\)，当\(n>N_0\)时，都有\(a_n\geqslant b_n\)且\(\lim\limits_{n\to\infty}a_n=a,\lim\limits_{n\to\infty}b_n=b\)，则\(a\geqslant b\).
【证明】用反证法，假设\(a<b\)，由性质3，\(\exists N_1\)，当\(n>N_1\)时，都有\(a_n<b_n\)
取\(N_2=\max\{N_0,N_1\}\)，当\(n>N_2\)时，\(a_n\geqslant b_n,a_n<b_n\)，矛盾，假设不成立
则\(a\geqslant b\).
【注意】若条件中的\(a_n\geqslant b_n\)改成\(a_n>b_n\)，结论是否可以改成\(a>b\)？不能改，反例：\(a_n=\frac{1}{n},b_n=-\frac{1}{n}\)，显然\(\frac{1}{n}>-\frac{1}{n}(n>1)\)，\(\lim\limits_{n\to\infty}\frac{1}{n}=0,\lim\limits_{n\to\infty}(-\frac{1}{n})=0\)，即\(a=b=0\).