【深度学习数学基础:高等数学】【苏德矿高等数学】第4讲:数列极限定义-1
2. 数列极限
数列极限是整个微积分的核心。它的思想贯穿整个微积分之中。
数列极限是最基本的、最核心的、最重要的、最难的。
2.1 数列
【定义】无限排列的一列数\(a_1,a_2,\cdots,a_n,\cdots\)就称为数列,记作\(\{a_n\}\),称\(a_n\)为数列的通项。
【定义】\(y=f(x),x\in\boldsymbol{D}\),特别地\(\boldsymbol{D}=\{1,2,3,\cdots,n,\cdots\}=\mathbb{N}\),\(y=f(x),x\in\mathbb{N}\),改写为\(y=f(n),n\in\mathbb{N}\)(自变量取正整函数,\(n:1,2,3,\cdots,n,\cdots\),\(f(n):f(1),f(2),f(3),\cdots,f(n),\cdots\)),由于自变量\(n\)可以按照自然数的顺序排成无限列,相应地,它的函数值也可以拍成无限列,\(f(1),f(2),f(3),\cdots,f(n),\cdots\)就称为数列,记作\(\{f(n)\}\),\(f(n)\)就称为数列的通项。
【注】设\(f(n)=a_n\),两种定义都是对的,无非就是形式不同,即数列\(a_1,a_2,a_3,\cdots,a_n,\cdots\).
庄子说:一尺之棰,日取之半,万世不竭。(一尺长的棒子,每条取剩下的一半,这样下去,永远取不完),即
天数为\(n:1,2,3,\cdots,n,\cdots\),
手中棒子的长度\(\frac{1}{2},\frac{1}{2^2},\frac{1}{2^3},\cdots,\frac{1}{2^n},\cdots\)
趋势:极限为\(0\).
【例】\(1,\frac{1}{2},\frac{1}{3},\cdots,\frac{1}{n},\cdots\)
画数轴,随着\(n\)无限增大,这个项与0越来越无限接近。
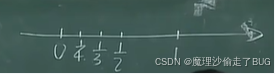
【例】\(1,-\frac{1}{2},\frac{1}{3},\cdots,\frac{(-1)^{n-1}}{n},\cdots\)
随着\(n\)无限增大,围绕着\(0\)两侧“跳来跳去”,极限为0

【例】\(\{1+\frac{(-1)^{n-1}}{n}\}\)的极限为1,并不是说极限都为0.
【例】\(\{n\}\)没有趋势(无穷大,无穷大不是数,所以称作没有趋势),也就是没有极限。
【例】\(1,-1,1,-1,\cdots,(-1)^{n-1},\cdots\)随着\(n\)无限增大,它不能与某个常数无限接近,它也是没有极限的。

因此我们只关心有趋势,也就是一个数列有极限,也就是随着\(n\)增大,数列的项与某个常数\(a\)无限地接近。
2.2 数列极限
【定义(定性分析)】设\(\{a_n\}\)是一个给定的数列,\(a\)是一个确定的常数,随着\(n\)无限增大,数列的项\(a_n\)与\(a\)无限地接近,称数列\(\{a_n\}\)的极限为\(a\),记作\(\lim\limits_{n\to\infty}a_n=a\)或\(a_n\to a(n\to\infty)\).
寻找用数学表达式给的定义,随着\(n\)无限增大,\(|a_n-a|\)与\(0\)无限地接近。\(\forall \varepsilon>0\)使得\(|a_n-a|<\varepsilon\)(你小我比你还小),找到一个自然数\(N\),当\(n>N\)都有\(|a_n-a|<\varepsilon\).
2.2.1 数列极限的定义
【定义】设\(\{a_n\}\)是一个给定的数列,\(a\)是一个确定的常数,若\(\forall \varepsilon>0\),相应地\(\exists\)自然数\(N\),当\(n>N\)时,都有\(|a_n-a|<\varepsilon\),称数列\(\{a_n\}\)的极限是\(a\),记作\(\lim\limits_{n\to\infty}a_n=a\)或\(a_n\to a(n\to\infty)\).
【例】\(1-1+1-1+\cdots+(-1)^{n-1}+\cdots\),求和。
【错解】\((1-1)+(1-1)+\cdots+(1-1)+\cdots=0\),\(1+(-1+1)+(-1+1)+\cdots+(-1+1)+\cdots=1\)
不能随便这样加括号(结合律),有限个数相加有结合律,无限个数相加不一定有结合律,其实这个是一个级数。
【例】\(1,-1,1,-1,\cdots,(-1)^{n-1},\cdots\)(不能取\(n\)大于偶数项,奇数项,极限是唯一的,不可能\(1\)是它的极限,\(-1\)也是它的极限)
对定义更进一步理解:
- 定义中的\(\forall \varepsilon>0\),从形式上,\(\varepsilon\)指的是一切正数,限制\(0<\varepsilon<1\)也可以(因为它仍然包含着0的右边的小区间,可以做到任意小的正数),但是不能限制\(\varepsilon>\)某个正数(这就没法衡量无限地接近,比如\(1,-1,1,-1,\cdots,(-1)^{n-1},\cdots\)这个数列,当\(\varepsilon>2\)时,\(|a_n-1|<2<\varepsilon\),但是这不能说明1就是它的极限),\(\varepsilon\)有时候也可以换成\(\varepsilon ^ 2,\sqrt{\varepsilon}\)(\(\varepsilon>0,\varepsilon^2 >0,\sqrt{\varepsilon}>0\),只要满足大于0的正数就行),但是\(\varepsilon\)不能换成\(\varepsilon +1\),因为\(\varepsilon+1>1\)了,\(|a_n-a|<\varepsilon\)也可以改成\(|a_n-a|\leqslant \varepsilon\).
- \(N\)的相应性,先有\(\varepsilon\),后有\(N\),再确定\(N\),使得\(n>N\)时,都有\(|a_n-a|<\varepsilon\)成立,也可以取\(N+1,N+2,\cdots\)作为新的\(N\)更能成立。甚至\(n>N\)可以改写\(n\geqslant N\),\(N\)也可以不是自然数,它只是一个下标的界限,假如\(n>3.5\),说明\(n\)从4开始也成立。
- 几何意义:\(\lim\limits_{n\to\infty}a_n=a\)即\(\forall \varepsilon>0,\exists N\),当\(n>N\)时都有\(|a_n-a|<\varepsilon\Leftrightarrow -\varepsilon<a_n-a<\varepsilon\Leftrightarrow a-\varepsilon<a_n<a+\varepsilon\Leftrightarrow a_n\in(a-\varepsilon,a+\varepsilon)\triangleq U(a,\varepsilon)\)【注1与注2】
\(U(a,\varepsilon)\)的外部只有有限项,其余项都在此邻域中,并且有无限项。
![ede6c4de7b7f4cefb48a0f949f93d09f]()
也就是对于\(a\)的任何\(\varepsilon\)邻域\(U(a,\varepsilon)\)在外部仅有数列的有限项,其余的项的统统在邻域内。如果这个邻域的半径取的越小,外面的项越多,再多也是有限项,其余的项统统在这个邻域内。
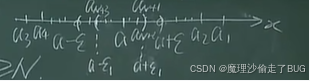
【注1】邻域与去心邻域
【定义】对区间我们常引入下面的记号,开区间\(\left(x_{0}-\delta, x_{0}+\delta\right) \xlongequal{\text { def }} U\left(x_{0}, \delta\right)(\delta>0)\)称为以\(x_0\)为中心,以\(\delta\)为半径的邻域,简称为\(x_0\)的\(\delta\)邻域。若不需要指明半径\(\delta\)时,记作\(U(x_0)\),称为\(x_0\)的某邻域。邻域一般是一个以\(x_0\)点为对称点的对称区间,如下图所示:
【定义】\(\left(x_{0}-\delta, x_{0}\right) \cup\left(x_{0}, x_{0}+\delta\right) \xlongequal{\text { def }} \stackrel{\circ}{U}\left(x_{0}, \delta\right)\)称为以\(x_0\)为中心,以\(\delta\)为半径的去心邻域(也叫空心邻域),简称为\(x_0\)的\(\delta\)去心邻域(空心邻域)。若不需要指明半径\(\delta\)时,记作\(\stackrel{\circ}{U}(x_0)\),称为\(x_0\)的某去心邻域(空心邻域)。去心邻域顾名思义是在邻域的基础上去掉对称中心\(x_0\)的区间,如下图所示:
2.2.2 分析法
【例】证明\(x>e\)时,\(x^2-3x+2>0\)
(使用分析法)
要证B成立,只要证A成立,指的是\(A\Rightarrow B\),反之不一定。即A成立是B成立的充分条件。
【证】要证\(x^2-3x+2>0\)成立
只要证\((x-1)(x-2)>0\)成立
只要证\(x<1\)或\(x>2\)成立
由\(x>e\Rightarrow x>2\Rightarrow x^2-3x+2>0\).

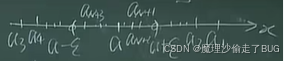



 浙公网安备 33010602011771号
浙公网安备 33010602011771号