【自学嵌入式笔记：模电】31. 常见的电学定律

31. 常见的电学定律

一、戴维宁定理（Thevenin's Theorem）

1. 核心思想

任何 线性含源二端网络（包含电源和电阻的两端子电路），可等效为一个 理想电压源（戴维宁电压 \(V_{\text{th}}\)）与一个 电阻（戴维宁电阻 \(R_{\text{th}}\)）的串联组合。

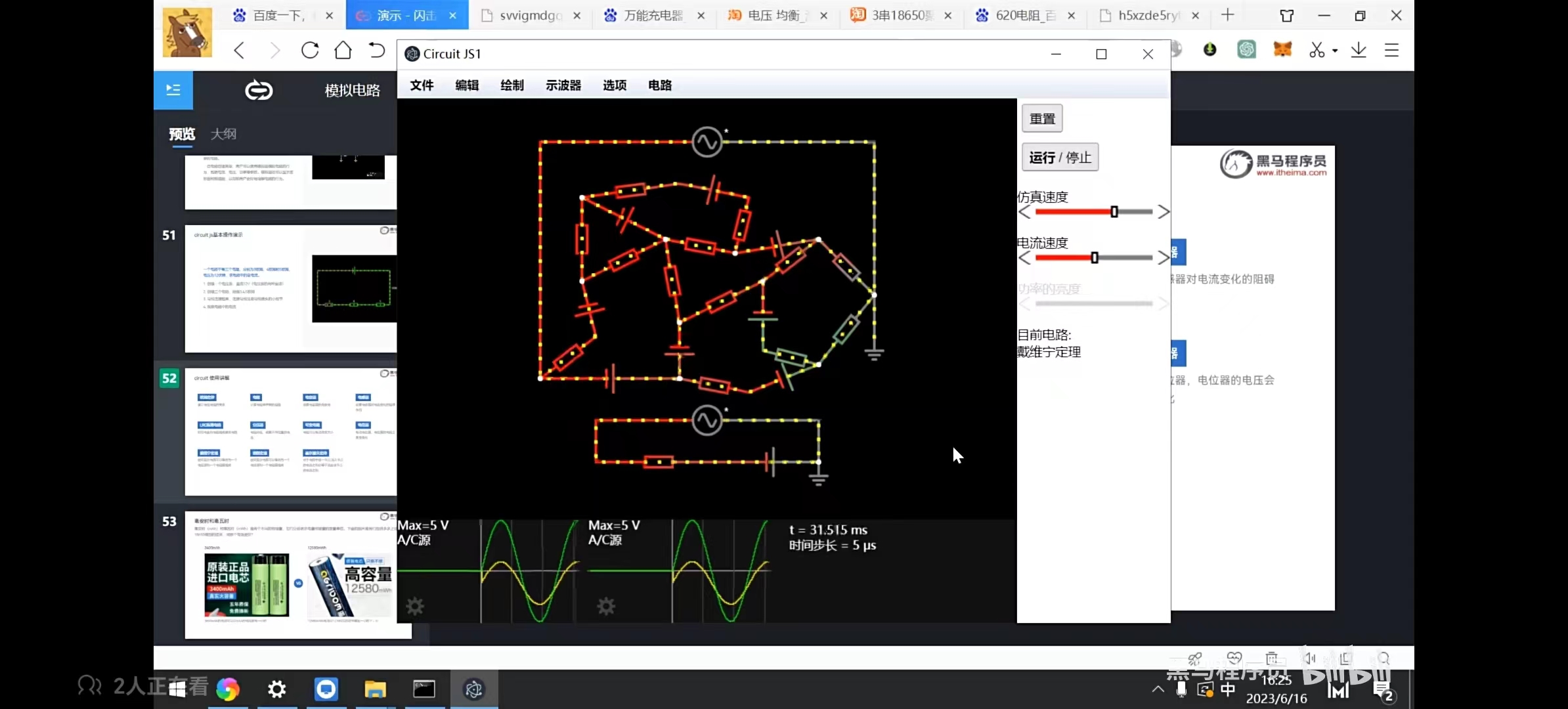
2. 仿真体现（图1复杂电路简化）

• 原电路：多电阻、电源组成的复杂网络（图1橙色连线电路）。
• 等效后：简化为 \(V_{\text{th}}\)（开路电压）和 \(R_{\text{th}}\)（等效电阻）串联，便于分析输出特性（如带负载时的电压变化）。

3. 关键步骤与公式

• 求戴维宁电压（\(V_{\text{th}}\)）：
  断开负载，测量二端网络的 开路电压（无负载时两端电压）。
• 求戴维宁电阻（\(R_{\text{th}}\)）：
  方法1：短路所有独立电源（电压源短路、电流源开路），测量二端网络的等效电阻。
  方法2：利用短路电流 \(I_{\text{sc}}\)，由 \(R_{\text{th}} = \frac{V_{\text{th}}}{I_{\text{sc}}}\) 计算（\(I_{\text{sc}}\) 为二端网络输出端短路时的电流）。

二、诺顿定理（Norton's Theorem）

1. 核心思想

任何 线性含源二端网络，可等效为一个 理想电流源（诺顿电流 \(I_{\text{n}}\)）与一个 电阻（诺顿电阻 \(R_{\text{n}}\)）的并联组合。

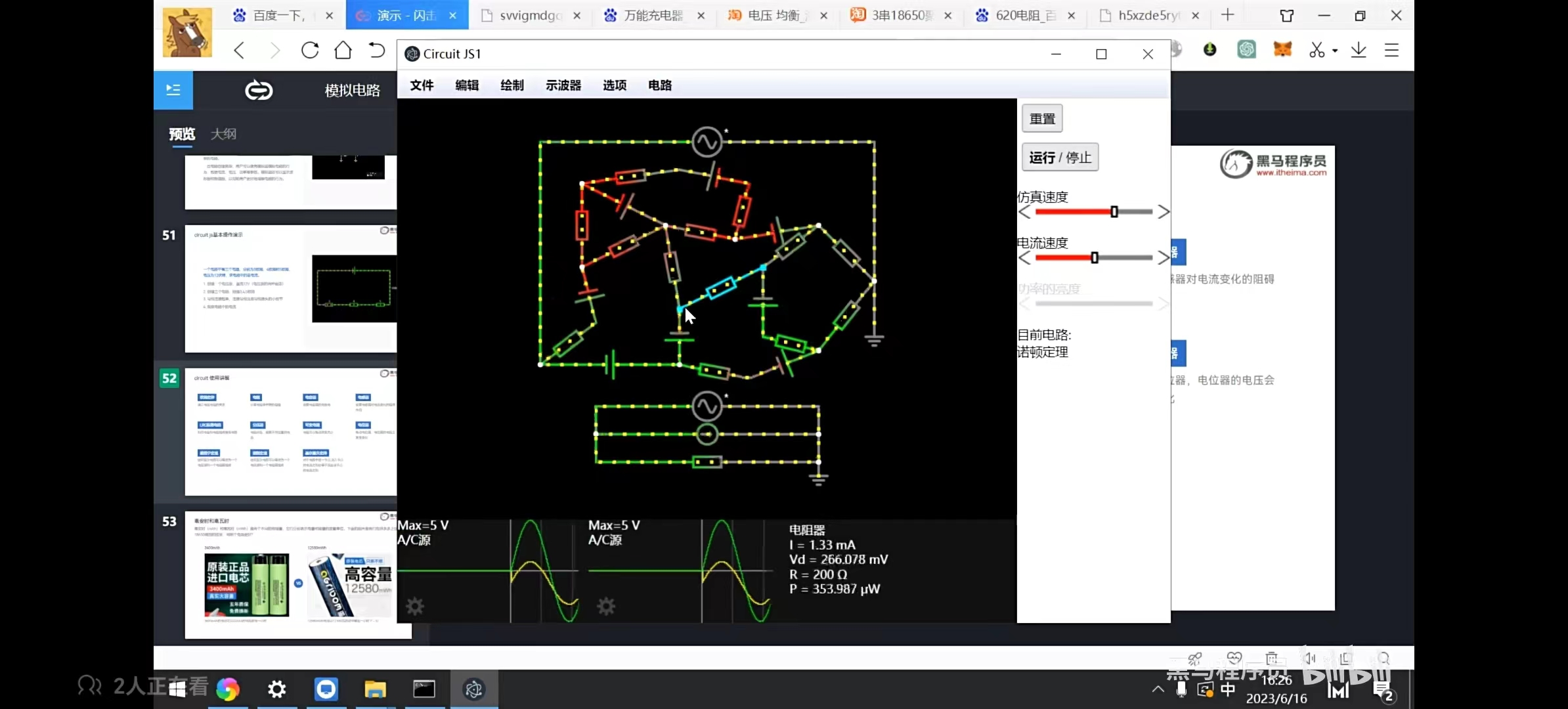
2. 仿真体现（图2复杂电路简化）

• 原电路：多电阻、电源组成的复杂网络（图2彩色连线电路）。
• 等效后：简化为 \(I_{\text{n}}\)（短路电流）和 \(R_{\text{n}}\)（等效电阻）并联，与戴维宁定理 对偶（\(V_{\text{th}} = I_{\text{n}} \cdot R_{\text{n}}\)，且 \(R_{\text{th}} = R_{\text{n}}\)）。

3. 关键步骤与公式

• 求诺顿电流（\(I_{\text{n}}\)）：
  短路二端网络输出端，测量 短路电流（输出端直接短接时的电流）。
• 求诺顿电阻（\(R_{\text{n}}\)）：
  同戴维宁电阻（因定理对偶性，\(R_{\text{n}} = R_{\text{th}}\)）。

三、基尔霍夫定律（Kirchhoff's Laws）

1. 电流定律（KCL：Kirchhoff's Current Law）

核心规则：对于电路中任一节点，流入节点的电流之和等于流出节点的电流之和，即：

\[\sum I_{\text{流入}} = \sum I_{\text{流出}} \]

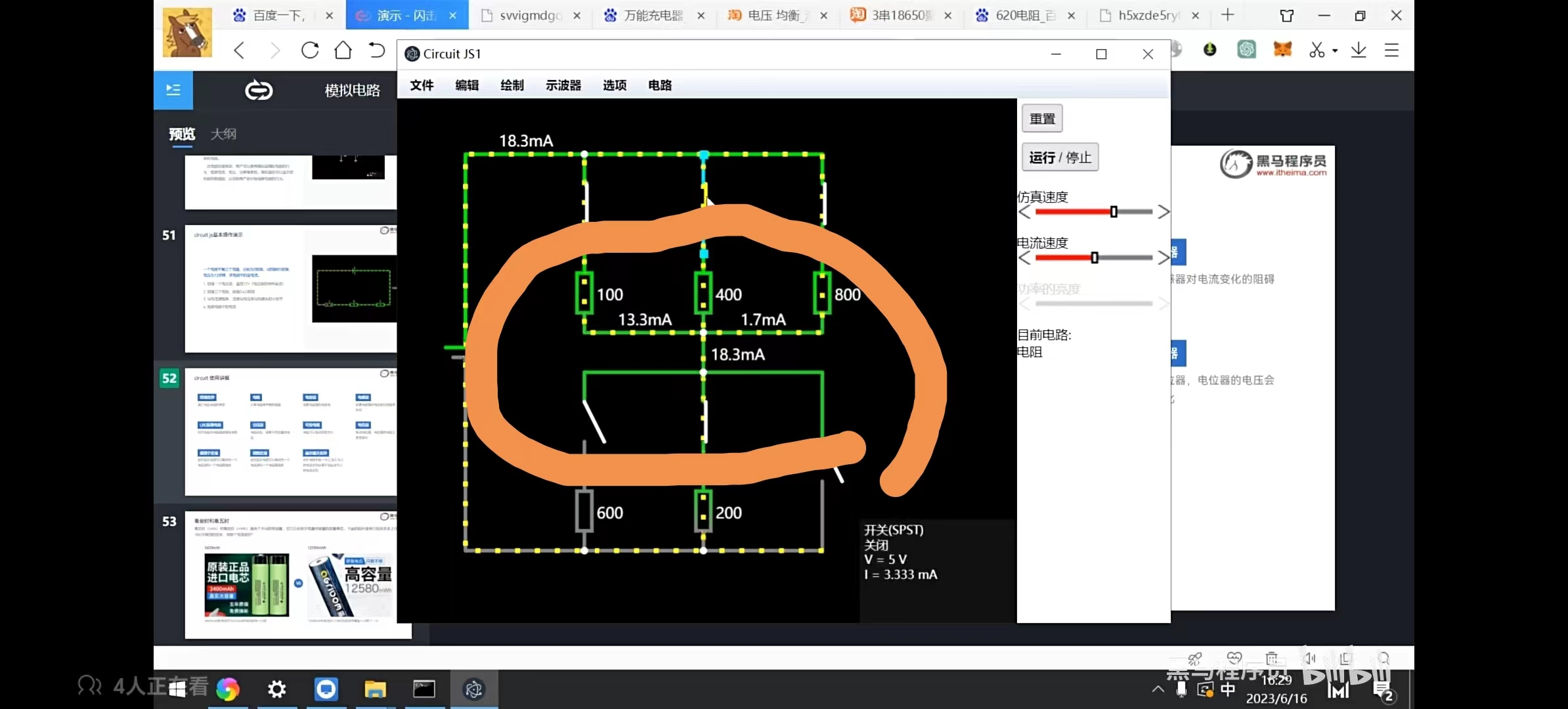
• 仿真体现（图3节点电流验证）：
  节点标注电流（如18.3mA流入），分支电流之和（13.3mA + 1.7mA + 3.333mA ≈ 18.3mA）与流入电流相等，验证KCL。

2. 电压定律（KVL：Kirchhoff's Voltage Law）

核心规则：对于电路中任一闭合回路，电压升之和等于电压降之和，即：

\[\sum V_{\text{升}} = \sum V_{\text{降}} \]

（或考虑方向时，\(\sum V = 0\)，电压升为正，电压降为负）

• 隐含验证（仿真回路电压）：
  电源电压等于回路中所有电阻的电压降之和（如5V电源 → 各电阻 \(V=IR\) 之和≈5V），验证KVL。

四、仿真工具的价值

1. 复杂电路简化：
   戴维宁/诺顿定理将多元件网络等效为2元件模型（电压源+电阻 / 电流源+电阻），大幅降低分析难度。

2. 定律直观验证：
   KCL/KVL通过仿真中 实时电流/电压标注（如图3节点电流、回路电压），直接验证理论，避免抽象推导。

五、总结

• 戴维宁与诺顿：对偶定理，分别用电压源、电流源等效复杂电路，简化分析。
• 基尔霍夫定律：电路分析基础，KCL约束节点电流，KVL约束回路电压。
• Circuit JS仿真：将抽象定理转化为可视化电流/电压动态，帮助新手理解理论与实际电路的联系。

（注：可通过调整仿真参数（如电阻值、电源电压），反复验证定理，强化理解。）