「NOIP赛前冲刺」LG126T1 折线

Solution

容易发现答案只有可能为 \(2,3,4\)，证明如下：

很明显答案不可能为 \(1\)，这里给出一种答案为 \(4\) 的满足条件的构造方案：

先找到一个点使得过这个点作一条平行 \(y\) 轴的线段，直线把所有点分成两部分（不包括直线上的点），两部分点的数量尽量平均分。

然后考虑把直线上的点分成两部分，容易发现两边点的数量之差最多为中间的点的数量，所以可以做出一条平行 \(x\) 轴的线段满足条件，再作一条平行 \(y\) 轴的线段，两条平行 \(y\) 轴的线段分开了两个部分，一条平行 \(x\) 轴的线段进行细微调整，可以看图理解：

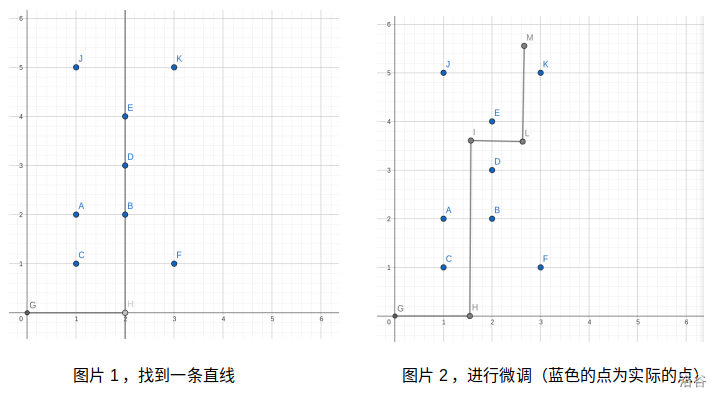
\(\text{Upd}\)：有的时候第一次竖着切时 \(4\) 次无法完成，但可以横着切，和上面同理。

所以题目转换成能判断否在 \(2\) 或 \(3\) 次内得到结果（否则就要四次）。

• 能否在 \(2\) 次得到结果

按照横坐标轴排序，求出对于某一时刻在这个点右侧的点的数量，若存在某一时刻使得答案为 \(\frac n 2\) 代表可以，纵坐标的处理相同（既可能时横着切也可能是竖着切）。

• 能否在 \(3\) 次得到结果

注意到只有先向上再向右和先向右再向上两种情况符合条件（先向下或先向左的情况还有多拐一个弯，需要 \(4\) 次），先考虑第一种情况：

还是先按照横坐标排序，从右往左枚举横坐标，容易发现纵坐标的选择有单调性（往右的横线越往上，包含的区间内点更多），可以二分纵坐标，接着可以用树状数组求出这个区间内点的个数。

具体的，把当前横坐标的右边的点的纵坐标加到树状数组里（横坐标不断左移，故每个点只加了一次），然后查询小于等于二分的纵坐标的点的数量即可，若存在某一时刻使得答案为 \(\frac n 2\) 代表可以，另一种情况同理，可以看图理解：

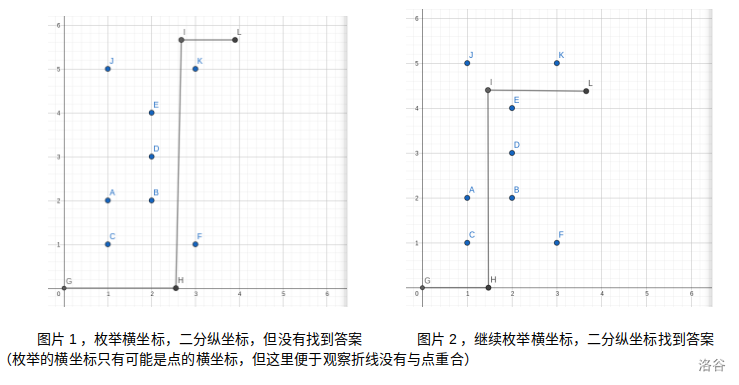
时间复杂度为 \(O(n\log^2n)\)，可以通过。

Code

判断能否为 \(2\) 的一种情况：

sort(a+1,a+n+1,cmp);
FOR(i,1,n)
{
	while(a[i].x==a[i+1].x&&i<n)i++;
	if(i==n/2)
	{
		puts("2");
		return;
	}
}

判断能否为 \(3\) 的一种情况：

sort(a+1,a+n+1,cmp);
ROF(i,n,1)
{
	while(a[i].x==a[i-1].x&&i>1)add(a[i].y),i--;
	add(a[i].y);
	int l=1,r=K;
	while(l<=r)
	{
		int mid=(l+r)/2;
		if(query(mid)==n/2)
		{
			puts("3");
			return;
		}
		if(query(mid)<n/2)
			l=mid+1;
		else r=mid-1;
	}
}