AT做题记录3

特别鸣谢

介于本人才疏学浅，有些题参考了一些大佬题解，在此提出感谢（排名不分前后）：
https://blog.csdn.net/write_1m_lines/article/details/118545542 作者：@GoodCoder666

ABC205D - Kth Excluded(*713)

Problem

给出 \(n\) 个数 \(a_i\) ，\(q\) 次询问，每次问除了这些数的第 \(k\) 大的正整数是什么。

Solution

注意到题目已经将 \(a_i\) 排好序，所以直接记 \(sum_i\) 表示 \(a_i-a_{i-1}\) 的前缀和，每次在 \(sum_i\) 里二分 \(k\)，即可算出第 \(k\) 大数在 \(a_w\) 和 \(a_{w+1}\) 之间，进而可得出答案。

ABC205E - White and Black Balls(*2025)

Problem

给出 \(n\) 个白球，\(m\) 个黑球以及一个常数 \(k\)，问你有多少种排列方式使得 \(\forall i\in[1,n+m]，w_i\le b_i+k\)，其中 \(w_i\) 表示在排列的第 \(i\) 个球以及它之前的白球个数，\(b_i\) 表示在排列的第 \(i\) 个球以及它之前的黑球个数。

答案与 \(10^9+7\) 取模。

Solution

考虑 dp，不妨设 \(f_{i,j}\) 表示用了 \(i\) 个白球和 \(j\) 个黑球满足条件的方案数，很明显有

\[f_{i,j}=f_{i,j-1}+f_{i-1,j}*[i\le j+k] \]

即在原先的基础上增加黑球一定符合条件，但增加白球不一定。

时间复杂度为 \(O(n^2)\) 无法 AC，考虑优化。

直接优化并没有什么办法，注意观察递推式，\((i,j)\) 都是从 \((i,j-1)\) 和 \((i-1,j)\) 转移过来的，所以可以把题目转化为从 $(0,0) $ 到 \((n,m)\) 的方案数（\(x\) 代表 \(w_i\)，\(y\) 代表 \(b_i\)），但不能经过直线 \(y=x+k\)，如下图：

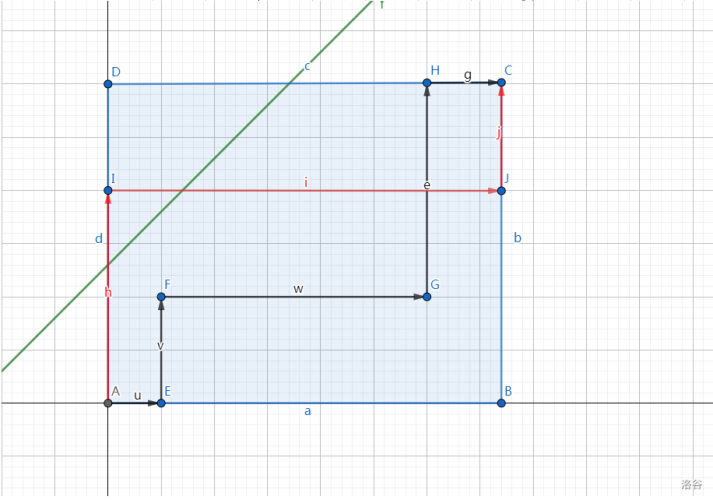
黑色的方案是合法的，但红色的方案不合法。

考虑做点 \((0,0)\) 关于 \(y=x+k+1\) 的对称点 \((-k-1,k+1)\)，那么从 \((-k-1,k+1)\) 到 \((n,m)\) 的每种方案都对应着一条从 \((0,0)\) 到 \((n,m)\) 且经过直线 \(y=x+k\) ，没有重复和遗漏的，如下图：

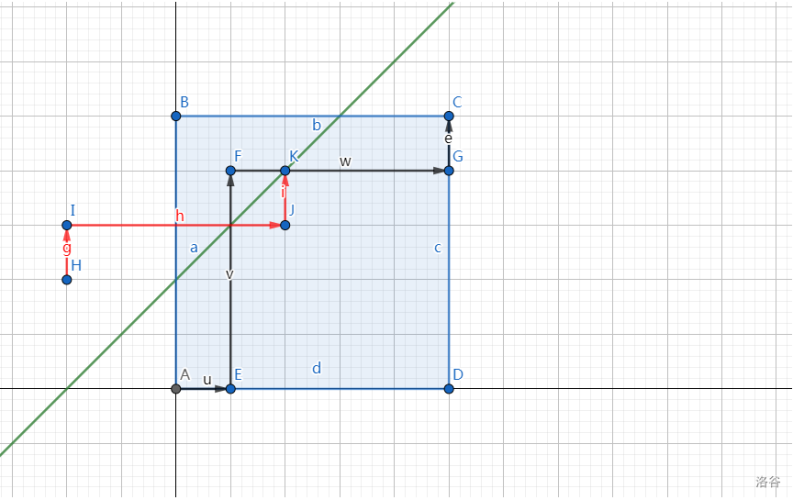
注意到是可以碰到 \(y=x+k\) 这一条直线的（即 \(w_i=b_i+k\)），所以只有碰到 \(y=x+k+1\) 才算不合法，所以做关于 \(y=x+k+1\) 的对称点。

从 \((0,0)\) 到 \((n,m)\) 的方案数为 \(\dbinom{n+m}{m}\) ，所以答案为 \(\dbinom{n+m}{m}-\dbinom{n+m}{m+k+1}\) 直接逆元求解即可。