P1600 [NOIP 2016 提高组] 天天爱跑步解析-树上差分+全局桶

思维难度：cf2300+

实现方案：贡献计算

方法：线段树合并或者树上差分+桶的统计

思路点补充：

按照题目的设定，如果一个观察员 \(j\) 能够观察到某个人经过，说明 \(j\)一定在第 \(i\)个人的路径上。

树上的路径是唯一确定的，由此可以得到两种情况。

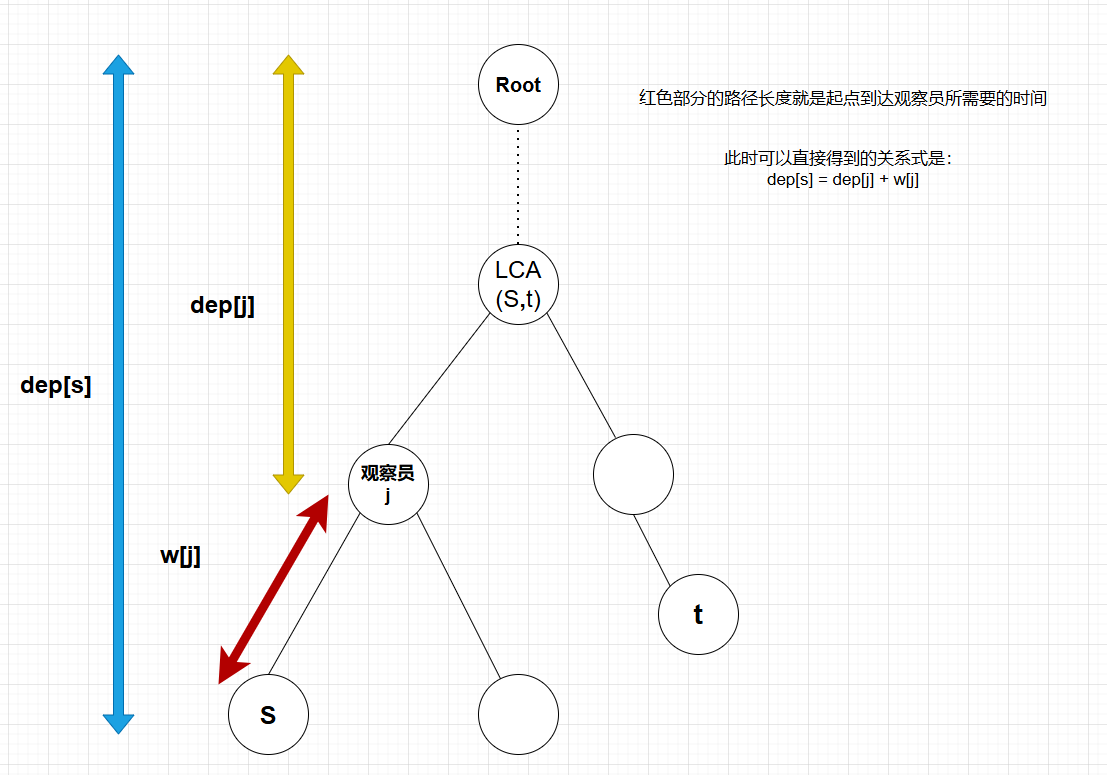
情况一：观察员 \(j\) 此时在 \(s\) 到 \(lca\) 的路径上（包括 \(lca\) ）。

此时我们可以直接得到关系式：\(dep_s = dep_j + w_j\)。

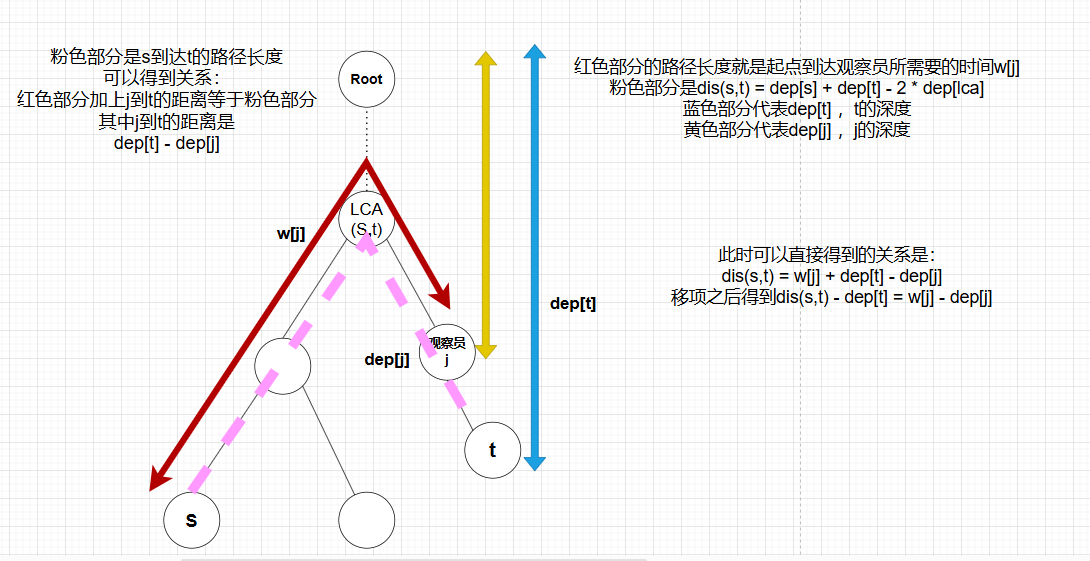
情况二：观察员 \(j\) 此时在 \(t\) 到 \(lca\) 的路径上（不包括 \(lca\) ）。

此时我们得到关系式：\(dis(s,t) - dep_t = w_j - dep_j\)。

公式 \(1\) ：\(dep_s = dep_j + w_j\)。

公式 \(2\) ：\(dis(s,t) - dep_t = w_j - dep_j\)。

观察这两个公式，我们将所有的不同的参数放在两端，此时式子等号左边是 \(s\) 到 \(t\) 的路径上的答案，右边是观察员 \(j\) 的答案。

所以我们看到上述两个公式的左边之后，$ dep_s $ 和 \(dis(s,t) - dep_t\) 都是固定值。

也就是对于观察员 \(j\) ，只要找到其子树上是否找到两个点的路径 \(s\) 到 \(t\) 是否满足公式 \(1\) 和 公式 \(2\) 即可。

但是这样实际求解的效率极低。

不妨反向考虑每条路径对于 所有观察点的影响：

观察下图，我们可以知道需要找到观察员是否对于每条路径满足上述两个公式。

用公式 \(1\) 作为样例，这个公式 \(dep_s = dep_j + w_j\) 存在的有效时间是 \(s\) 到 \(lca\) ，超过这个范围就不生效了。

相当于答案 \(dep_s\) 在 \(s\) 处出现，在 \(lca\) 处消失。

问题可以转换为 在观察员 \(j\) 这个点的子树内，有多少个点满足 \(dep_i\)等于观察员的 \(dep_j + w_j\)。

此时我们只需要将\(s\) 到 \(lca\) 上进行点权都加上 \(dep_s\) ，这样就可以得到正确的影响范围，从而将该问题转换为子树问题。

换句话来说：

公式 \(1\) 的左边 \(dep_s\) 理解为第一类特殊的数字，存在的范围是 \(s\) 到 \(lca\) , 题目统计的是每个观察点子树内有多少个存在的第一类数字。

公式 \(2\) 的右边 \(dis(s,t) - dep_t\) 理解为第二类特殊的数字，存在的范围是 \(s\) 到 \(lca\) 的直接儿子节点，题目统计的是每个观察点子树内有多少个存在的第二类数字。

两类数相加就是答案。

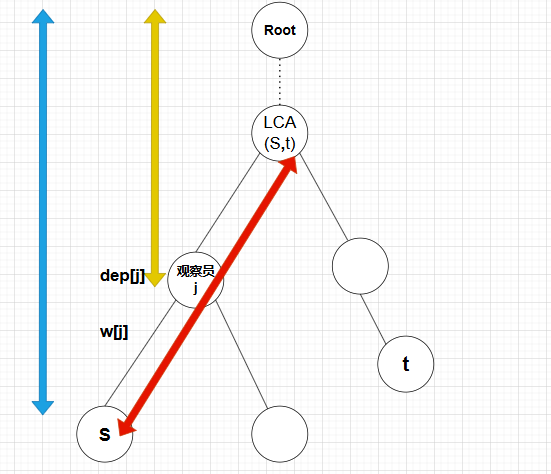
基本思路理清楚了，回归到子树问题本身，如何求解对应阶段的答案，为什么需要将 \(dep_s\) 这个当作第一类数当作增量将 \(s\) 到 \(lca\) 的点权都进行修改。

这是因为我们必须将影响的范围全部标记。比如在下图之中，答案对于两个观察员都有影响。

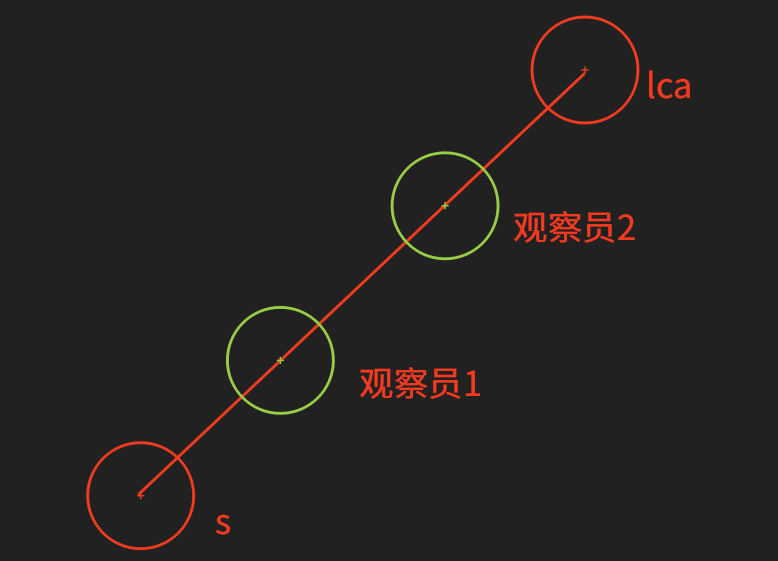
标记的做法这里我们可以利用树上点差分的方式，这里需要大家熟知差分的本质，假设有一个人从 \(s\) 移动到 \(lca\) 需要将 \(dep_s\) 的影响带给途径的所有点。

此时我们可以理解为这个人在 \(s\) 点拿到了 \(dep_s\) ，但是从 \(lca\) 之后点就不属于这个路径范围了，立马对 \(lca\) 的父亲减去 \(dep_s\)。

树上差分不在同一子树内也是同样的理解。

具体实现分析

vector<int> add1[maxn], sub1[maxn]; // 差分记录s 到 lca的影响 
vector<int> add2[maxn], sub2[maxn]; // 差分记录lca子节点 到 t的影响 

add1[s].push_back(dep[s]);
sub1[fa_lca].push_back(dep[s]); // 差分当前链
add2[t].ush_back(dep[s] - 2 * dep[LCA]);
sub2[LCA].push_back(dep[s] - 2 * dep[LCA]);
// 准确定位差分的每个点  到达该点了，就直接该add的add，该删除的删除
其中s到lca的差分是[s]++，[fa_lca]--
其中lca的子节点到t的差分是sub2[LCA]--，add2[t]++

最后如何统计子树答案？

使用两个全局桶，记录两种方向下，u这个观察点dep[u] + w[u]以及w[u] - dep[u] + n的出现次数
    子树内的数值出现次数，直接采用前后的状态之差
    比如递归到3的时候，cnt1统计的次数是5次
    回溯到3的时候，cnt1变成了10次，说明这个地方出现了5条路径满足答案。

参考代码：

#include <bits/stdc++.h>
using namespace std;
const int maxn = 3e5 + 7;
int n, m, t, dep[maxn], dp[maxn][21];
int w[maxn];
int cnt1[maxn << 1];
int cnt2[maxn << 1];
int ans[maxn];
queue<int> q;
vector<int> add1[maxn], sub1[maxn];
vector<int> add2[maxn], sub2[maxn];
vector<int> G[maxn];
bool vis[maxn];
void add_edge(int u, int v)
{
    G[u].push_back(v);
    G[v].push_back(u);
    return;
}
void dfs(int u, int fa) // u的父节点是fa
{
    dp[u][0] = fa;        // 边界条件
    dep[u] = dep[fa] + 1; // 深度
    for (int i = 1; (1 << i) <= dep[u]; i++)
    {
        dp[u][i] = dp[dp[u][i - 1]][i - 1];
    }
    for (int i = 0; i < G[u].size(); i++) // 循环u的相邻结点
    {
        int v = G[u][i];
        if (v != fa)
        {
            dfs(v, u);
        }
    }
    return;
}
int lca(int x, int y) // 约定y的深度更大
{
    if (dep[x] > dep[y])
    {
        swap(x, y);
    }
    for (int i = 20; i >= 0; i--) // 让y往上跳与x高度一致
    {
        if (dep[x] <= dep[dp[y][i]])
        {
            y = dp[y][i]; // y跳
        }
    }
    if (x == y)
    {
        return x;
    }
    for (int i = 20; i >= 0; i--) // x、y一起往上跳
    {
        if (dp[x][i] != dp[y][i])
        {
            x = dp[x][i];
            y = dp[y][i];
        }
    }
    return dp[x][0];
}

void dfs2(int u, int fa)
{
    int val1 = cnt1[dep[u] + w[u]];
    int val2 = cnt2[w[u] - dep[u] + n]; // 防止负数，加一个n
    for (int i = 0; i < G[u].size(); i++)
    {
        int v = G[u][i];
        if (v == fa)
        {
            continue;
        }
        dfs2(v, u);
    }
    for (int i = 0; i < add1[u].size(); i++)
    {
        cnt1[add1[u][i]]++;
    }
    for (int i = 0; i < sub1[u].size(); i++)
    {
        cnt1[sub1[u][i]]--;
    }
    for (int i = 0; i < add2[u].size(); i++)
    {
        cnt2[add2[u][i] + n]++;
    }
    for (int i = 0; i < sub2[u].size(); i++)
    {
        cnt2[sub2[u][i] + n]--;
    }
    ans[u] += cnt1[dep[u] + w[u]] - val1 + cnt2[w[u] - dep[u] + n] - val2; //  记录两个点的前后状态之差
    return;
}

int main()
{
    cin >> n >> m;
    for (int i = 1; i < n; i++)
    {
        int u, v;
        cin >> u >> v;
        add_edge(u, v);
    }
    for (int i = 1; i <= n; i++)
    {
        cin >> w[i];
    }
    dfs(1, 0);
    for (int i = 1; i <= m; i++)
    {
        int u, v;
        cin >> u >> v;
        int LCA = lca(u, v);
        int fa_lca = dp[LCA][0];
        add1[u].push_back(dep[u]);
        sub1[fa_lca].push_back(dep[u]); // 差分当前链
        add2[v].push_back(dep[u] - 2 * dep[LCA]);
        sub2[LCA].push_back(dep[u] - 2 * dep[LCA]);
    }
    dfs2(1, 0);
    for (int i = 1; i <= n; i++)
    {
        cout << ans[i] << ' ';
    }
    return 0;
}