宁盾杯-Crypto-BabyLCG

宁盾杯-Crypto-BabyLCG

第一次遇到LCG算法，先学习。

$$
X_{n+1}=(aX_n + b)\quad mod \quad m
$$

LCG（linear congruential generator）线性同余算法，是一种产生伪随机数的方法。

线性同余法最重要的是定义了三个整数，乘数 a、增量 b和模数 m，其中a,b,m是产生器设定的常数。
为了方便理解，我打个比方
假设现在有随机数X1=1234，乘数a=2，增量b=3，模数m=1000
那么下一个随机数X2=(2*1234+3)%1000=2471%1000=471
————————————————
版权声明：本文为CSDN博主「小健健健」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/superprintf/article/details/108964563

解题用到的公式:

目的	公式
Xn+1反推出Xn	Xn=(a-1 (Xn+1 - b))%m
求a	a=((Xn+2-Xn+1)(Xn+1-Xn)-1)%m
求b	b=(Xn+1 - aXn)%m
求m	tn=Xn+1-Xn，m=gcd((tn+1tn-1 - tntn) , (tntn-2 - tn-1tn-1))

具体六种题型详见原文

好叻，现在来做题

from secret import flag
from random import choice
from Crypto.Util.number import *
from base64 import *

base = choice([1, 2, 3])
if base == 1:
    flag = bytes_to_long(b16encode(flag))
elif base == 2:
    flag = bytes_to_long(b32encode(flag))
else:
    flag = bytes_to_long(b64encode(flag))


class LCG:
    def __init__(self, seed, multiplier, increment, modulus):
        self.state = seed
        self.multiplier = multiplier
        self.increment = increment
        self.modulus = modulus

    def up(self):
        self.state = (self.state * self.multiplier + self.increment) % self.modulus
        return self.state


LcG = LCG(flag, getPrime(512), getPrime(512), getPrime(512))
gift = []
for i in range(10):
    gift.append(LcG.up())
print('gift = ' + str(gift[7:]))
print('modulus = ' + str(LcG.modulus))

'''
gift = [6998668913539720854586318078964097924269535810376945153454874762880079122855229214946631470660390590416643009737549611992701041036474370166645418280901007, 
1892495848465417621576404191173925036164429140753793974334011134456947671358112732280576451200645683850307514019481657914071929753218355720294738264191434, 
4484145280982945455195043055386171233045034368064549769546029757634338455428186964514780286626949054244061700559656648067211088700781715028531671487463280]
modulus = 10450107588012697221920913365783869685974004783055148990692823980665238902913056762076796149418379728342781425496729735242364725136682283797430781849299753
'''

很明显，已知m，output[7]，output[8]，output[9]，求flag

根据LCG原理，如果output[0]比作Xn+1，flag就是Xn
$$
X_n=(a^{-1}(X_{n+1} - b)) \quad % \quad m
$$
由此可以知晓解题思路为通过output[7]，output[8]，output[9]求解a，b

通过a，b，m，反推8次获得flag

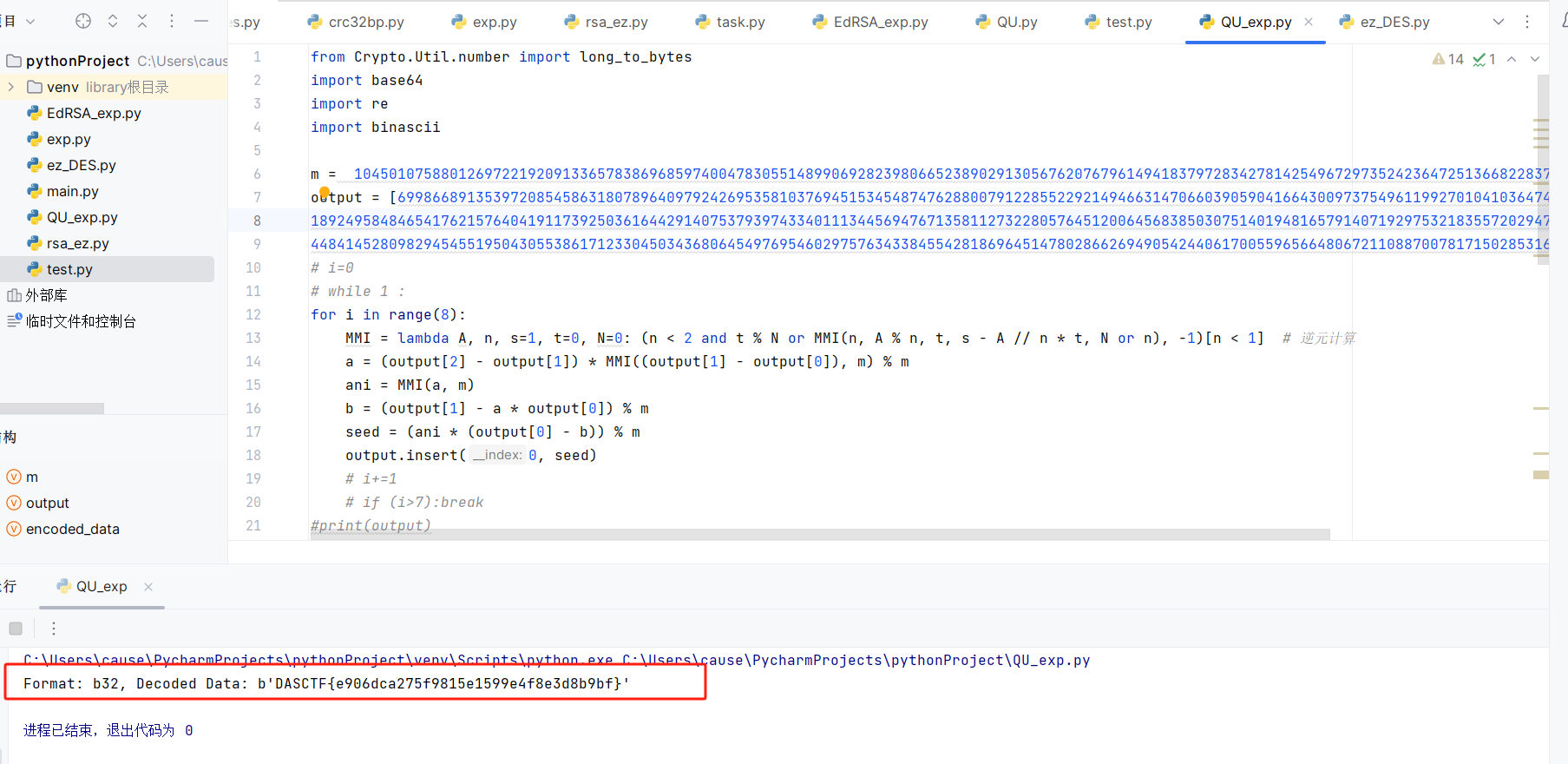
from Crypto.Util.number import long_to_bytes
import base64
import re
import binascii

m =  10450107588012697221920913365783869685974004783055148990692823980665238902913056762076796149418379728342781425496729735242364725136682283797430781849299753
output = [6998668913539720854586318078964097924269535810376945153454874762880079122855229214946631470660390590416643009737549611992701041036474370166645418280901007,
1892495848465417621576404191173925036164429140753793974334011134456947671358112732280576451200645683850307514019481657914071929753218355720294738264191434,
4484145280982945455195043055386171233045034368064549769546029757634338455428186964514780286626949054244061700559656648067211088700781715028531671487463280]

for i in range(8):
    MMI = lambda A, n, s=1, t=0, N=0: (n < 2 and t % N or MMI(n, A % n, t, s - A // n * t, N or n), -1)[n < 1]  # 逆元计算
    a = (output[2] - output[1]) * MMI((output[1] - output[0]), m) % m
    ani = MMI(a, m)
    b = (output[1] - a * output[0]) % m
    seed = (ani * (output[0] - b)) % m
    output.insert(0, seed)

encoded_data = long_to_bytes(output[0])
for format in ["b64", "b32", "b16"]:
    try:
        decoded_data = getattr(base64, format + "decode")(encoded_data)
        if re.findall(b'CTF', decoded_data):
            print(f"Format: {format}, Decoded Data: {decoded_data}")
    except (binascii.Error,TypeError):
        pass

#Format: b32, Decoded Data: b'DASCTF{e906dca275f9815e1599e4f8e3d8b9bf}'