OO Unit1 总结
综述
第一单元的任务主要是进行包含幂运算的表达式化简,在随后几次作业的迭代开发后可以实现支持幂函数,括号嵌套,有限个自定义函数(及其嵌套),三角函数与求和函数。主体架构采用递归下降算法拆分表达式为Expr(表达式)、Term(项)、Factor(因子),后对于拆分好的字符串进行计算、化简与合并同类项。
一、程序架构分析
HW1
-
实现一个包含加、减、乘与乘方的表达式展开与化简,允许出现至多一层括号
-
代码架构
-
基本类及其行为
![]()
-
其中,可以分为递归下降部分、存储因子及计算两部分。
Lexer与Parser为递归下降法先拆分后按类读取字符串的过程,对表达式进行初步的解析。通过递归下降算法,将表达式分为Expr,Term与Variable,其内部逻辑与指导书中形式化表示贴合。
其中Expr表示:空白项 [加减 空白项] 项 空白项 | 表达式 加减 空白项 项 空白项
Term→ [加减 空白项] 因子 | 项 空白项 * 空白项 因子
Variable→ 变量因子 | 常数因子 | 表达式因子。
其中,最为关键的基本项为Variable类,用以表示最基本同时涵盖所有类型因子的情况:
我为其设置了三个元素来充分的表示:Cofficient(常数),Power(幂次),Negitive(符号),在合并同类相前,式子应被化简为n个variable相加减的形式。由此,我完成了作业一在架构方面的基本构思。
关于拆分后表达式的计算:
初步的考虑采用递归的方法将因子计算,返回上一层项中计算,最后返回表达式类,再合并同类项输出结果。最后因为时间(和心态QWQ)的问题,没有在架构中成功实现,而采用了将每个项中的元素暴力相乘,最后一并在expr中进行加减,过长的method与多层嵌套的ifelse结构,为无穷的bug制造了绝佳的机会…也预示了后续迭代的痛苦重构:(
-
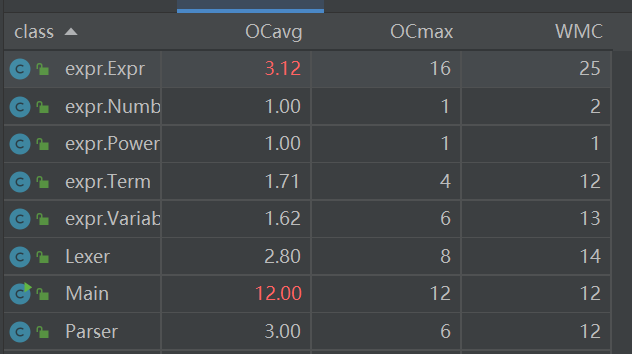
复杂度分析
![]()
(非常惊人的数据,由于在Main中做了大量字符串的预处理,当做一次教训了
-
化简与合并同类项
-
存储的容器十分关键,用Hashmap存储Variable,key为power,value为Cofficient,方便计算与合并
-
一些细节的优化如:cofficient = 1、power = 0的情况,与
x**2->x*x;
-
HW2
-
内容简述:在HW1的基础上增加了三角函数、求和函数与自定义函数,多余括号仍为最多一层。
对于求和函数与自定义函数,我采用不失语义的带入法(通俗而言就是带括号的带入加细节处理),对表达式进行预处理,转化为符合HW1形式化表述的的表达式后,套用第一次的计算与化简。
-
代码架构分析
![]()
在基本类中增加了三角函数类与自定义函数类,对于新增项各自放到类中处理完后,以表达式的形式添加到原有表达式中,同样参与计算即可。此时,计算部分的巨大mothed还没有重构(由于懒惰hhh),好在各种细节注意到了,没有在互测环节伤痕累累。
-
复杂度分析
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Lexer.Lexer(String) | 0 | 1 | 1 | 1 |
| Lexer.getCos() | 8 | 5 | 3 | 6 |
| Lexer.getNumber() | 2 | 1 | 3 | 3 |
| Lexer.getPower() | 3 | 1 | 7 | 7 |
| Lexer.getSin() | 8 | 5 | 3 | 6 |
| Lexer.next() | 13 | 2 | 8 | 9 |
| Lexer.peek() | 0 | 1 | 1 | 1 |
| Parser.Parser(Lexer) | 0 | 1 | 1 | 1 |
| Parser.parseExpr() | 5 | 1 | 4 | 4 |
| Parser.parseFactor() | 25 | 9 | 14 | 14 |
| Parser.parseTerm() | 2 | 1 | 3 | 3 |
| advance.preCheck() | 8 | 1 | 8 | 9 |
| advance.setStr(String) | 0 | 1 | 1 | 1 |
| cal.cal1() | 27 | 1 | 8 | 8 |
| cal.setExpr(Expr) | 0 | 1 | 1 | 1 |
| expr.Cos.Cos(String) | 0 | 1 | 1 | 1 |
| expr.Expr.Expr() | 0 | 1 | 1 | 1 |
| expr.Expr.addTerm(Term) | 0 | 1 | 1 | 1 |
| expr.Expr.cal(Term) | 91 | 1 | 19 | 19 |
| expr.Expr.getMi() | 0 | 1 | 1 | 1 |
| expr.Expr.getTerm() | 0 | 1 | 1 | 1 |
| expr.Expr.getTerms() | 0 | 1 | 1 | 1 |
| expr.Expr.setMi(int) | 0 | 1 | 1 | 1 |
| expr.Expr.toString() | 3 | 1 | 3 | 3 |
| expr.Function.getExpr() | 0 | 1 | 1 | 1 |
| expr.Function.getItem() | 0 | 1 | 1 | 1 |
| expr.Function.getName() | 0 | 1 | 1 | 1 |
| expr.Function.setExpr(String) | 0 | 1 | 1 | 1 |
| expr.Function.setName(char) | 0 | 1 | 1 | 1 |
| expr.Function.setVariable(String) | 4 | 3 | 2 | 3 |
| expr.Number.Number(BigInteger) | 0 | 1 | 1 | 1 |
| expr.Number.toString() | 0 | 1 | 1 | 1 |
| expr.Sin.Sin(String) | 0 | 1 | 1 | 1 |
| expr.Term.Term() | 0 | 1 | 1 | 1 |
| expr.Term.addFactor(Factor) | 0 | 1 | 1 | 1 |
| expr.Term.addNegitive(boolean) | 0 | 1 | 1 | 1 |
| expr.Term.caculate() | 11 | 2 | 6 | 6 |
| expr.Term.getFactors() | 0 | 1 | 1 | 1 |
| expr.Term.getNegitive() | 0 | 1 | 1 | 1 |
| expr.Term.toString() | 3 | 1 | 3 | 3 |
| expr.Variable.Variable(BigInteger, int) | 0 | 1 | 1 | 1 |
| expr.Variable.addCofficient(BigInteger) | 0 | 1 | 1 | 1 |
| expr.Variable.addCos(String, int) | 7 | 3 | 3 | 6 |
| expr.Variable.addNegitive1(boolean) | 0 | 1 | 1 | 1 |
| expr.Variable.addSin(String, int) | 7 | 3 | 3 | 6 |
| expr.Variable.copyCos(HashMap<String, Integer>) | 0 | 1 | 1 | 1 |
| expr.Variable.copySin(HashMap<String, Integer>) | 0 | 1 | 1 | 1 |
| expr.Variable.getCoefficient() | 0 | 1 | 1 | 1 |
| expr.Variable.getCos() | 0 | 1 | 1 | 1 |
| expr.Variable.getNegitive1() | 0 | 1 | 1 | 1 |
| expr.Variable.getPower() | 0 | 1 | 1 | 1 |
| expr.Variable.getSin() | 0 | 1 | 1 | 1 |
| expr.Variable.toString() | 24 | 2 | 11 | 12 |
复杂度重灾区仍然是计算cal部分,没有和整体架构融为一体的计算模块虽然完成了相关任务,但是却非常不利于迭代开发。
-
化简与合并同列项
由于表达式最终仍被化简为
Variable+Variable+的形式,故新添加的因子同样应该以一定的形式储存在Variable中
对于Sin与Cos,采用
Hashmap<String,Integer>以三角函数内expr为key,三角函数的power为value,方便合并同类项
HW3
-
内容分析
在作业二的基础上增添多层括号嵌套与自定义函数嵌套
-
代码架构
与第二次的UML图几乎完全相同,计算的环节完全重构,采用后缀表达式的方式来解决括号嵌套的问题,而对于表达式嵌套,采用递归带入的方式处理,总体由第二次作业迭代开发完成。
-
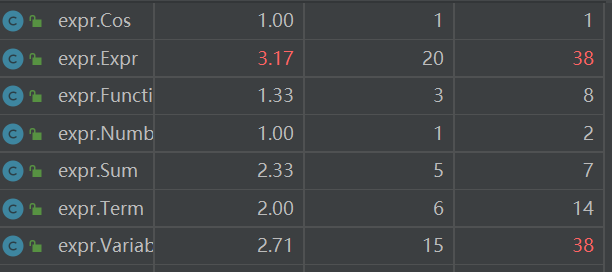
复杂度分析
![]()
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Func.Func(HashMap<Integer, Function>, String) | 0 | 1 | 1 | 1 |
| Func.checkFunc() | 155 | 18 | 29 | 31 |
| Lexer.Lexer(String) | 0 | 1 | 1 | 1 |
| Lexer.getCos() | 8 | 5 | 3 | 6 |
| Lexer.getNumber() | 2 | 1 | 3 | 3 |
| Lexer.getPower() | 3 | 1 | 7 | 7 |
| Lexer.getSin() | 8 | 5 | 3 | 6 |
| Lexer.next() | 13 | 2 | 8 | 9 |
| Lexer.peek() | 0 | 1 | 1 | 1 |
| Parser.Parser(Lexer) | 0 | 1 | 1 | 1 |
| Parser.parseExpr() | 5 | 1 | 4 | 4 |
| Parser.parseFactor() | 27 | 9 | 15 | 15 |
| Parser.parseTerm() | 1 | 1 | 2 | 2 |
| advance.preCheck() | 8 | 1 | 8 | 9 |
| advance.setStr(String) | 0 | 1 | 1 | 1 |
| caculate.cal() | 23 | 4 | 16 | 16 |
| caculate.getCos() | 8 | 5 | 3 | 6 |
| caculate.getNumber() | 2 | 1 | 3 | 3 |
| caculate.getSin() | 8 | 5 | 3 | 6 |
| caculate.muLit(Expr, Expr) | 21 | 1 | 8 | 8 |
| caculate.setExpr(String) | 0 | 1 | 1 | 1 |
| sinCos.simPlify() | 18 | 7 | 6 | 9 |
| sinCos.sinCos(String) | 0 | 1 | 1 | 1 |
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| expr.Cos.Cos(String) | 0 | 1 | 1 | 1 |
| expr.Expr.Expr() | 0 | 1 | 1 | 1 |
| expr.Expr.addStandExpr(Variable) | 0 | 1 | 1 | 1 |
| expr.Expr.addTerm(Term) | 0 | 1 | 1 | 1 |
| expr.Expr.copyExpr(Expr) | 0 | 1 | 1 | 1 |
| expr.Expr.fan() | 4 | 1 | 3 | 3 |
| expr.Expr.getMi() | 0 | 1 | 1 | 1 |
| expr.Expr.getStandExpr() | 0 | 1 | 1 | 1 |
| expr.Expr.getTerm() | 0 | 1 | 1 | 1 |
| expr.Expr.getTerms() | 0 | 1 | 1 | 1 |
| expr.Expr.setMi(int) | 0 | 1 | 1 | 1 |
| expr.Expr.toString() | 11 | 1 | 6 | 6 |
| expr.Function.getExpr() | 0 | 1 | 1 | 1 |
| expr.Function.getItem() | 0 | 1 | 1 | 1 |
| expr.Function.getName() | 0 | 1 | 1 | 1 |
| expr.Function.setExpr(String) | 0 | 1 | 1 | 1 |
| expr.Function.setName(char) | 0 | 1 | 1 | 1 |
| expr.Function.setVariable(String) | 4 | 3 | 2 | 3 |
| expr.Number.Number(BigInteger) | 0 | 1 | 1 | 1 |
| expr.Number.toString() | 0 | 1 | 1 | 1 |
| expr.Sum.SumString() | 7 | 1 | 5 | 5 |
| expr.Sum.setBegin(BigInteger) | 0 | 1 | 1 | 1 |
| expr.Sum.setSum(String) | 0 | 1 | 1 | 1 |
| expr.Term.Term() | 0 | 1 | 1 | 1 |
| expr.Term.addFactor(Factor) | 0 | 1 | 1 | 1 |
| expr.Term.addNegitive(boolean) | 0 | 1 | 1 | 1 |
| expr.Term.caculate() | 11 | 2 | 6 | 6 |
| expr.Term.getFactors() | 0 | 1 | 1 | 1 |
| expr.Term.getNegitive() | 0 | 1 | 1 | 1 |
| expr.Term.toString() | 3 | 1 | 3 | 3 |
| expr.Variable.Variable(BigInteger, int) | 0 | 1 | 1 | 1 |
| expr.Variable.addCofficient(BigInteger) | 0 | 1 | 1 | 1 |
| expr.Variable.addCos(String, int) | 7 | 3 | 3 | 6 |
| expr.Variable.addNegitive1(boolean) | 0 | 1 | 1 | 1 |
| expr.Variable.addSin(String, int) | 7 | 3 | 3 | 6 |
| expr.Variable.copyCos(HashMap<String, Integer>) | 0 | 1 | 1 | 1 |
| expr.Variable.copySin(HashMap<String, Integer>) | 0 | 1 | 1 | 1 |
| expr.Variable.getCoefficient() | 0 | 1 | 1 | 1 |
| expr.Variable.getCos() | 0 | 1 | 1 | 1 |
| expr.Variable.getNegitive1() | 0 | 1 | 1 | 1 |
| expr.Variable.getPower() | 0 | 1 | 1 | 1 |
| expr.Variable.getSin() | 0 | 1 | 1 | 1 |
| expr.Variable.setMultiItem(boolean) | 0 | 1 | 1 | 1 |
| expr.Variable.toString() | 35 | 2 | 14 | 15 |
二、bug分析
第一次作业:
计算过程过于暴力以至于式子太长时出现多种情况的处理不好,一直在修改cal内部的逻辑。
第二次作业:
强测错了四个点,互测时被hack了一刀,一共查出了三个bug:
-
符号的问题,在expr中toString中多设置了符号的判断,导致错误。
-
第二个是类似于x*-1的问题
-
第三个是式子结果为0的情况,应判断空串情况再输出。
第三次作业:
强测错了四个点,互测时被hack了sum的范围,用的long类型,找到了同房间小伙伴的一些bug,主要有以下:
-
大数bug,互测的同学都在爆int爆long(互相伤害),使用了int或long存储数据,而非BigInteger造成了bug。
-
sum函数的bug:出现s1n,s2n的情况;上界小于下界的情况;BigInteger负数的情况;sum嵌套的情况…
-
零次幂bug,这部分bug第一次作业应该就修过了,但是遇到sin和cos函数,自定义和sum函数参数替换,以及层层嵌套关系后,有时零次幂又会输出奇怪的结果。
三、Hack策略分析
我一般只是手动输入一些数据,比如x**0、x*-2*-1、1**+0001等等一些简单易错的数据,还有一些边界大数的数据,充分利用代码架构中最冗杂逻辑性较差的部分找出来漏洞去hack,用自己的bug样例…在对自己的程序做了较多测试,积累了一定bug的经验之后,对于相似架构的代码可以尝试同样的方法hac。
四、收获总结
在第一单元的三次作业中,我逐渐学习到了面向对象编程的思想和方法,深刻体会到到了一个良好的架构对程序迭代开发的重要性,设计是重中之重,在开发之初就应该保有着为迭代做准备的想法,同时代码风格检查也让我改正了很多不好的习惯。以下是我在第一单元的主要收获:
-
在着手开始写之前,把基本的代码架构想好,不可以边写边重构:( 把各个类、函数的关系搞清楚.
-
仔细阅读指导书,深入理解形式化表述的深层逻辑,思考程序设计的目的,与迭代的可能方向,在指导书中有着出题者的意图与做法的而推荐,都应该仔细理解消化。
-
重构要趁早,赶到第三次作业再去面对一个迭代性能几乎为0的代码内心实际是崩溃的,如果没有办法再一开始就避免无法迭代需要重构的情况,就在发现问题后立马着手去做,对于坏的架构疯狂丰富细节的意义不是很大
五、心得体会
因为寒假的Pre没有认真做好,前三周经历了一个边学基础知识边处理问题的痛苦经历,思路的匮乏和无限的重构,耗费了很多的时间,但是收获也很多,可以说是一个被逼着快速入门的过程了QWQ 另外,我充分感觉到了面向对象这门课对个人代码能力的要求,作业发下来后对着题目坐牢一天,才能开始着手实现,有时需要和同学讨论,求教助教等等,实现前的压力和实现后的成就感反复叠加…第二单元增加对于架构与迭代的考虑,避免走第一单元过度重构的弯路。






 浙公网安备 33010602011771号
浙公网安备 33010602011771号