动态规划之一阳指——转移状态的横向对比
先粗略介绍解决动态规划的整个过程,这里提供两个解决思路:
第一种,固定模式:
1 确定状态
需要两个意识:
最后一步:最优策略的最后一步。
子问题:子问题与原问题类似
2 设置转移方程
3 添加初始条件和边界情况,比如题目的限制条件等等
4 计算优化,空间、时间上
第二种,递归改写,但是对于有些问题递归是不太好写的。
1 设计暴力算法——递归(递归的思路相当清晰,写出来的代码相当短小精悍)
2 找到冗余设计并存储状态(-维,二维,三维数组,甚至用Map )
3 更改递归式(状态转移方程),存储递归返回的值。
4 自底向上计算最优解(编程方式)
从局部上看,本文主要想解决的问题是如何分析动态规划的状态问题,状态是解决转移方程的关键钥匙,不论采用何种方法解决问题,状态是一定要事先确定的!
设置状态——
一般是采用数组存储的方式:
1 一维数组
每个元素 f[ i ] 的含义
2 二维数组
f[ i ][ j ],i * j 个元素,每个元素的含义
DP类型
最大最小值规划:
LintCode 669: Coin Change
你有三种硬币,分别面值2元,5元和7元, 每种硬币都有足够多,买一本书需要27元
如何用最少的硬币组合正好付清,不需要对方找钱。
输入: [1, 2, 5] 11 输出: 3 解释: 11 = 5 + 5 + 1
输入: [2] 3 输出: -1
分析状态:由于是线性序列,可以采用一维数组 f[ ],f[ ] 存储硬币个数,故设
状态 f[ X ] = 最少用多少枚硬币拼出 X,X 为数值;
硬币有三种:2、5、7,
拼出X所需要的最少硬币数:
f[ X ] = min{ f[ X - 2 ] + 1, f[ X - 5 ] + 1, f[ X - 7 ] + 1 }
有一个机器人的位于一个 m × n 个网格左上角。
机器人每一时刻只能向下或者向右移动一步。机器人试图达到网格的右下角。
问有多少条不同的路径?
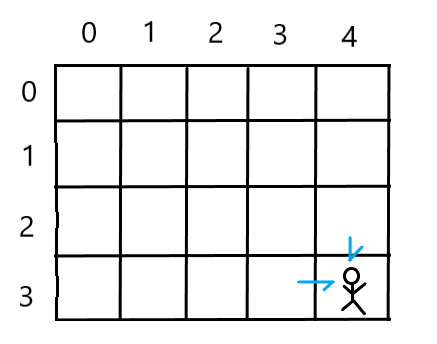
eg1: Input: n = 1, m = 3 Output: 1 Explanation: Only one path to target position. eg2: Input: n = 3, m = 3 Output: 6 Explanation: D : Down R : Right 1) DDRR 2) DRDR 3) DRRD 4) RRDD 5) RDRD 6) RDDR
分析:网格结构,坐标的移动需坐标 ( x, y) 的变化,故开辟一个二维数组 valueDp[ ][ ]。但是这个数组如何设置含义呢?
最后一步:无论机器人用何种方式到达右下角,总有最后挪动的一步;
每一步向右或者向下,右下角坐标设为 ( m - 1, n - 1 ),那么前一步机器人一定是在 (m - 2, n - 1 )或者 (m - 1, n - 2)
状态:设 f[ i ][ j ]为机器人有多少种方式从左上角走到 (i, j);
自然地,f[ i - 1 ][ j ] 表示机器人有多少种方式走到 (i - 1, j);
自然地,f[ i ][ j - 1] 表示机器人有多少种方式走到 (i, j - 1)
那么,对于任意一个格子( i, j ),有两个方向可以到达此位置,根据加法组合原理,可以推导出转移方程:
f[ i ][ j ] = f[ i - 1 ][ j ] + f[ i ][ j - 1]
存在型DP
LintCode 116. 跳跃游戏 jump-game
给出一个非负整数数组,你最初定位在数组的第一个位置;
数组中的每个元素代表你在那个位置可以跳跃的最大长度。
判断你是否能到达数组的最后一个位置。
e.g.1: 输入 : [2,3,1,1,4] 输出 : true e.g.2: 输入 : [3,2,1,0,4] 输出 : false
分析:题目是一维数组,判断结果是否可达,所以采用一维数组状态
状态:设 f[ j ] 表示青蛙能不能跳到石头 j;
那么选择上一个石头 i 的条件是什么?为什么上一个石头不是 j - 1 呢?这是设置变量 i 的原因。
抛出来三个问题:
怎么选择石头 i;能不能跳到石头 i;最后一步的距离不能超过 ai ;
OR 0<=i<j ; f[ i ] i + a[ i ] >= j
就是构成转移方程的元素:
f[ j ] = OR 0<=i<j (f[ i ] AND i + a[ i ] >= j )
LintCode 191. 乘积最大子序列 maximum-product-subarray
给定a[0], ... a[n-1],找出一个序列中乘积最大的连续子序列(至少包含一个数)。
样例 1: 输入:[2,3,-2,4] 输出:6 样例 2: 输入:[-1,2,4,1] 输出:8
分析状态:其乘积最大,为一维数组,记为 f[ ],
乘积的结果和数字的正负号相关,当前值为正数最大值,再乘一个负值,就变成负数最小值了,再乘负数,变成正数最大值;
考虑到一个数组存储空间和 序列相关的话,不够用,所以选取两个一维数组,f[ ] 和 g[ ]
f[ j ] = 以 a[ j ]结尾的连续子序列的最大乘积
g[ j ] =以 a[ j ]结尾的连续子序列的最小乘积
故状态:
f[ j ] = 以 a[ j ] 结尾的连续子序列的最大乘积
情况1 :子序列就是a[ j ]本身,a[ j ];
情况2 :以a[ j - 1 ]结 尾的连续子序列的最大/最小乘积,乘上 a[ j ],max{ a[ j ] * f[ j - 1 ], a[ j ] * g[ i - 1 ] }
转移方程:f[ j ] = max{ a[ j ],max{ a[ j ] * f[ j - 1 ], a[ j ] * g[ i - 1 ] } | j > 0 }
坐标型动态规划:数组下标 [ i ][ j ] 即坐标 (i, j)
LintCode 115: Unique Paths II
给定 m 行 n 列的网格,有一个机器人从左上角(0,0)出发,每一步可以向下或者向右走一步
网格中有些地方有障碍,机器人不能通过障碍格
问有多少种不同的方式走到右下角
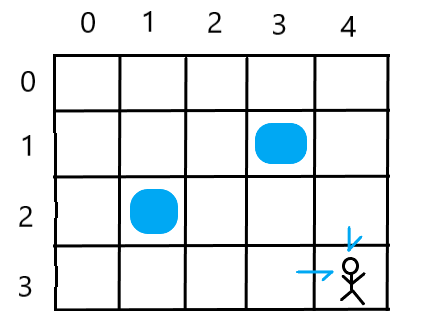
Example 1: Input: [[0]] Output: 1 Example 2: Input: [[0,0,0],[0,1,0],[0,0,0]] Output: 2 Explanation: Only 2 different path.
状态分析:假设坐标为 (x, y),记为 (i, j)
最后一步一定是从左边 (i, j - 1) 或上边 (i - 1, j) 过来
设状态 f[ i ][ j ] 表示从左上角有多少种方式走到格子 (i, j);
那么 (i, j - 1) 记为 f[ i ][ j - 1 ] 表示从左边有多少种方式走到格子 (i, j - 1);
(i - 1, j) 记为 f[ i - 1 ][ j ] 表示从上边有多少种方式走到格子 (i - 1, j)
所以状态转移方程为:
f[ i ][ j ] = f[ i - 1 ][ j ] + f[ i ][ j - 1 ]
但是如果遇到障碍怎么办?则加上限制条件:
f[ i ][ j ] = 0
初始条件和边界条件不在本文的讨论范围内。
LintCode 515 Paint House
这里有 n 个房子在一列直线上,现在我们需要给房屋染色,分别有红色蓝色和绿色。每个房屋染不同的颜色费用也不同,你需要设计一种染色方案使得相邻的房屋颜色不同,并且费用最小,返回最小的费用。
费用通过一个 n x 3 的矩阵给出,比如 cost[ 0 ][ 0 ] 表示房屋 0 染红色的费用,cost[ 1 ][ 2 ] 表示房屋 1 染绿色的费用。
样例 1: 输入: [[14,2,11],[11,14,5],[14,3,10]] 输出: 10 解释: 第一个屋子染蓝色,第二个染绿色,第三个染蓝色,最小花费:2 + 5 + 3 = 10. 样例 2: 输入: [[1,2,3],[1,4,6]] 输出: 3
显然题目中是二维数组,故状态也要开辟一个二维数组空间
当前房子 i 所要涂的颜色与前一个房子 i - 1 涂的颜色相关,
只有三个颜色,所以二维元素个数为 3.
即可以设置状态: valueDp[ i ][ j ] 为第 i 个房子油漆颜色 j 所需要的花费;
当前房子为红色:
valueDp[ i ][ 0 ] = min{ valueDp[ i - 1 ][ 1 ] + cost[ i - 1 ][ 0 ], valueDp[ i - 1 ][ 2 ] + cost[ i - 1 ][ 0 ] };
当前房子为蓝色:
valueDp[ i ][ 1 ] = min{ valueDp[ i - 1 ][ 0 ] + cost[ i - 1 ][ 1 ], valueDp[ i - 1 ][ 2 ] + cost[ i - 1 ][ 1 ] };
当前房子为绿色:
valueDp[ i ][ 2 ] = min{ valueDp[ i - 1 ][ 0 ] + cost[ i - 1 ][ 2 ], valueDp[ i - 1 ][ 1 ] + cost[ i - 1 ][ 2 ] };
划分型
LintCode 512 Decode Ways
有一个消息包含A-Z通过以下规则编码
'A' -> 1
'B' -> 2
...
'Z' -> 26
现在给你一个加密过后的消息,问有几种解码的方式
样例 1: 输入: "12" 输出: 2 解释: 它可以被解码为 AB (1 2) 或 L (12). 样例 2: 输入: "10" 输出: 1
状态分析:字符的数值范围在 1 ~ 26,超过这个范围必然会被截断。
字符串的长度个数设置为 i ,对应的一维数组状态 f[ i ] = 字符长度为 i 有多少种解密方式
但是这个动态转移方程有点不太好想,可以假设数字串 S 前 i 个数字解密成字母串有 f[ i ] 种方式
f[ i ] = f[ i - 1 ] | S[ i - 1 ] 对应一个字母+ f[ i - 2 ] | S[ i - 2 ] S[ i - 1 ] 对应一个字母
LintCode 667. 最长的回文序列
给一字符串 s, 找出在 s 中的最长回文子序列的长度. 你可以假设 s 的最大长度不超过 1000.
样例1 输入: "bbbab" 输出: 4 解释: 一个可能的最长回文序列为 "bbbb" 样例2 输入: "bbbbb" 输出: 5
分析状态:
字符串需要转成字符数组便于取出具体的字符元素;
虽然是一维序列,但是对字符数组的操作是从两边进行的,所以需要设置二维数组来存储状态。
故设 transferDp[ i ][ j ]为 S[ i...j ] 的最长回文子串的长度,i j 为字符数组 S[ ] 的起始下标
当 S[ i ] == S[ j ] 时,字符数组 S,两边同时缩减一个字符,状态数组 + 2 ==> transferDp[ i + 1 ][ j - 1 ] + 2 ;
transferDp[ i ][ j ] = max{ transferDp[ i + 1][ j ], transferDp[ i ][ j - 1 ], transferDp[ i + 1 ][ j - 1 ] + 2 | S[ i ] == S[ j ] }

遍历过程如下图:
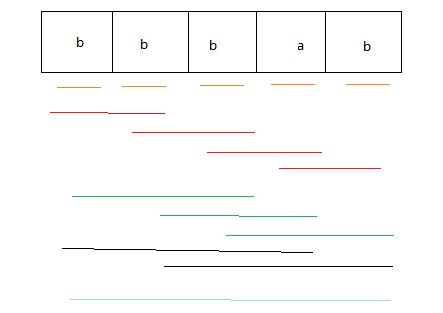
这里提醒重要的一点:状态数组一定要和实际意义结合起来,数组虽然可以存储值,但是与操作过程相违背,可以不用赋值。
transferDp[ i ][ j ] = 字符数组 i 至 j 之间的字符元素;transferDp[ ][ ] 的下三角元素就不存在实际意义,就可以不用赋值,可以写成:
for (int i = 0 ; i < n ; i++) {
for (int j = i; j < n; j++) {
valueDp[i][j] = -1;
}
}
练习:
LintCode 396 Coins In A Line III
给定一个序列 a[0], a[1], ... a[N-1]
两个玩家Alice和Bob轮流取数
每个人每次只能取第-一个数或最后一个数双方都用最优策略,使得自己的数字和尽量比对手大问先手是否必胜
如果数字和一样,也算先手胜
输入:[1,5, 233, 7] 输出: True (先手取走1, 无论后手取哪个,先手都能取走233)
答案:设 f[ i ][ j ] 为一方先手在面对 a[ i...j ] 这些数字时,能得到的最大的与对手的数字差


 浙公网安备 33010602011771号
浙公网安备 33010602011771号