逻辑回归

一、概述

1.1  模型间接

Logistic Regression 虽然被称为回归，但其实际上是分类模型，并常用于二分类；

Logistic 回归的本质是：假设数据服从这个分布（sigmoid函数），然后使用极大似然估计做参数的估计。

 

 

二、数学依据

2.1 sigmoid函数

 

 

 

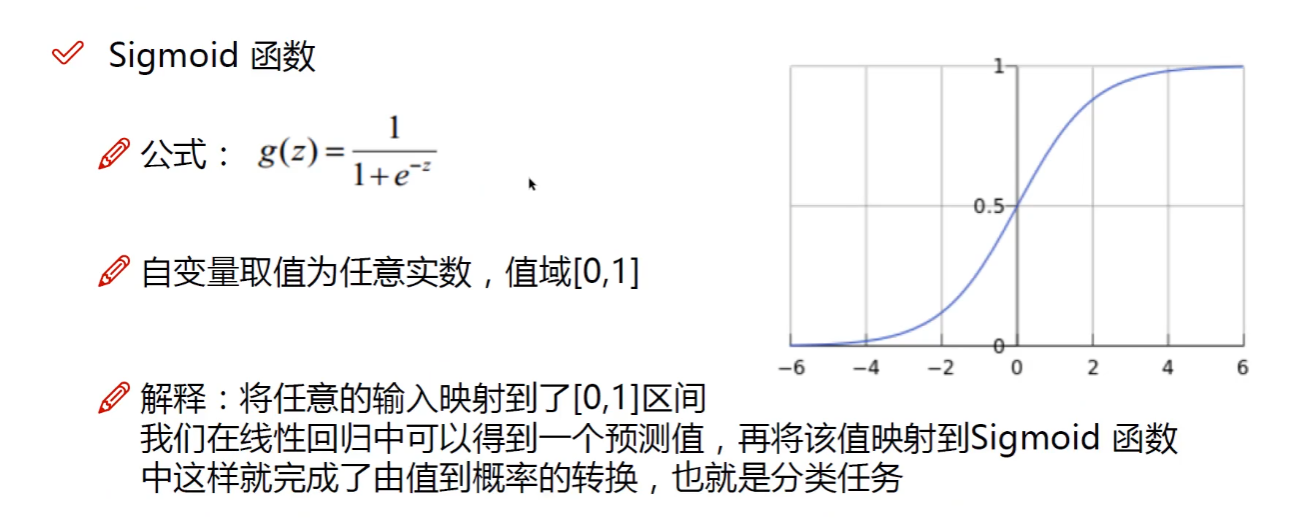
逻辑回归模型本质就是将线性回归模型通过Sigmoid函数进行了一个非线性转换，

得到一个介于0～1之间的概率值，对于二分类问题（分类0和1）而言，其预测分类为1（或者说二分类中数值较大的分类）的概率可以用如下所示的公式计算。

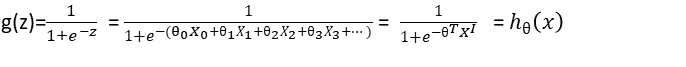
其中X₀ = 1 

 

 

 

 

 

 

 

 

 

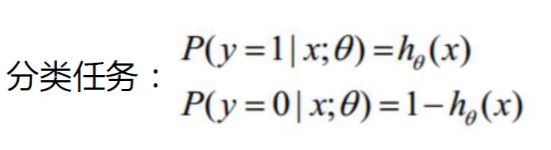
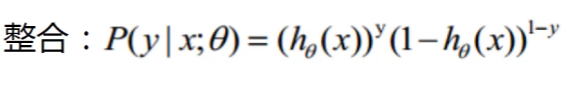
 2.2 似然函数

这一步的主要作用求出_^θ的值。

 原理参考：https://blog.csdn.net/u011508640/article/details/72815981

^{_{最大似然估计：当我们知道总体的概率分布模型的时候，但是不知道概率分布函数的参数的情况下，我们用样本来估计参数。}}

简单来说，就是通过确定分布函数的参数是多少的情况下，使得我们抽的当下样本的概率最大。

 

 

 

 

 

 

 

 

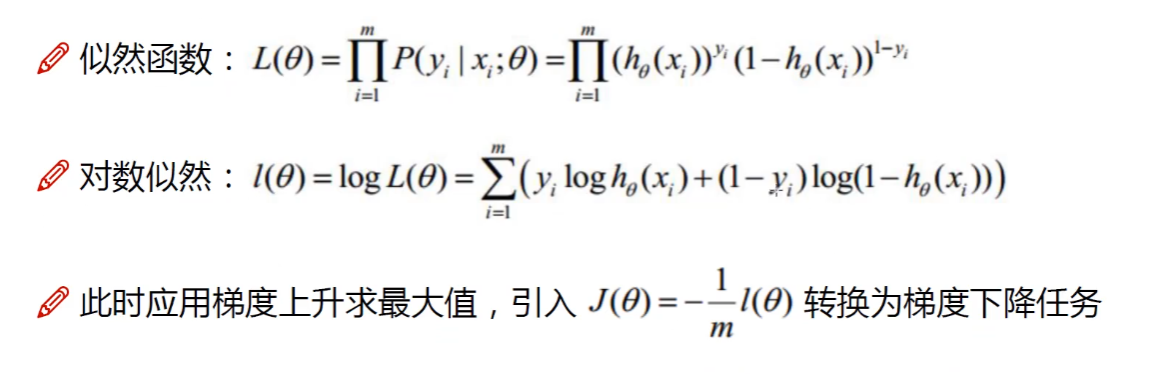
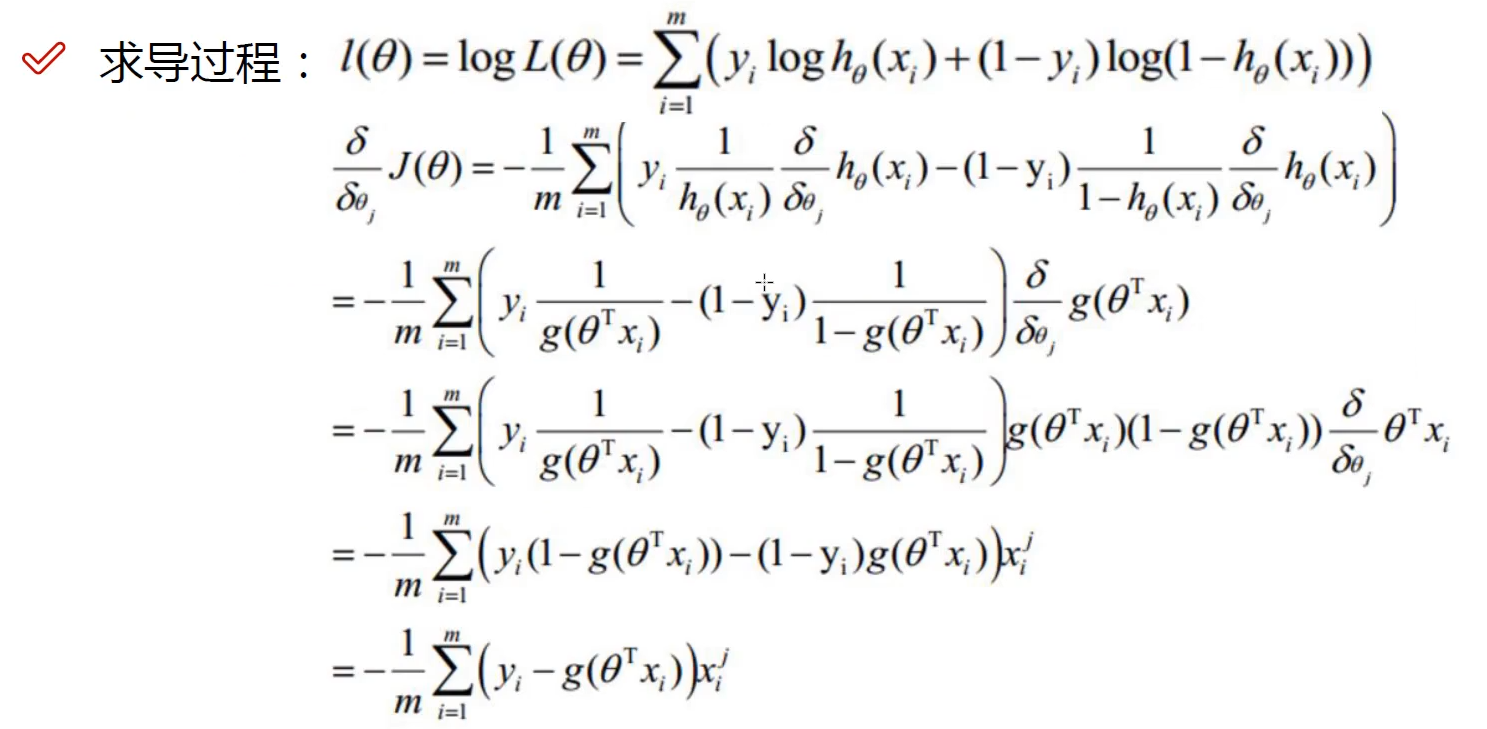
2.3 预测

通过极大似然估计求出θ_{^{的值，再将}}θ带入到sigmoid函数中，再讲测试集或者未来数据带入到sigmoid中，岂可求出预测值。

三、极简案例

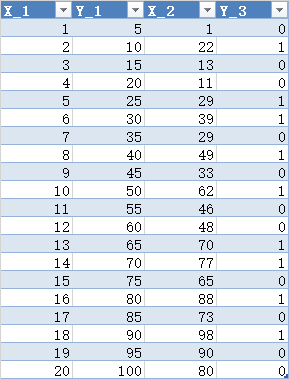
3.1 数据

Y_1  = X*5

Y_3 = IF(Y_1>X_2，0,1）

 

 

 

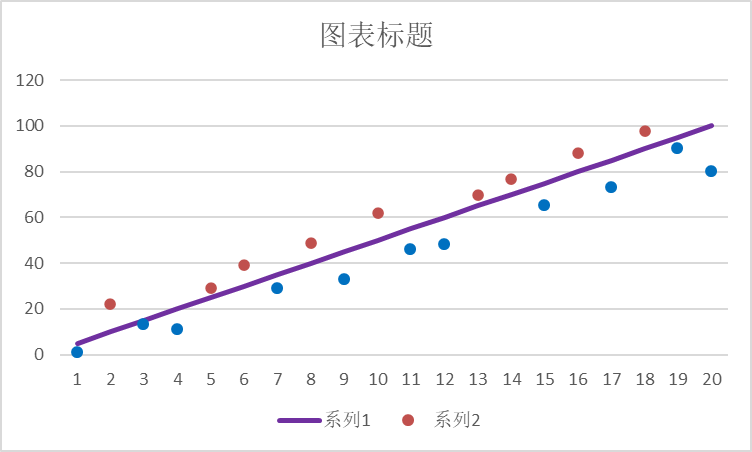
 3.2 图形展示

紫色是的直线是y = 5* X

圆点是X_1与X_2的点。

在紫色线上的标位红点，即Y_3为0

在紫色线下的标位蓝点，即Y_3为1

 

 

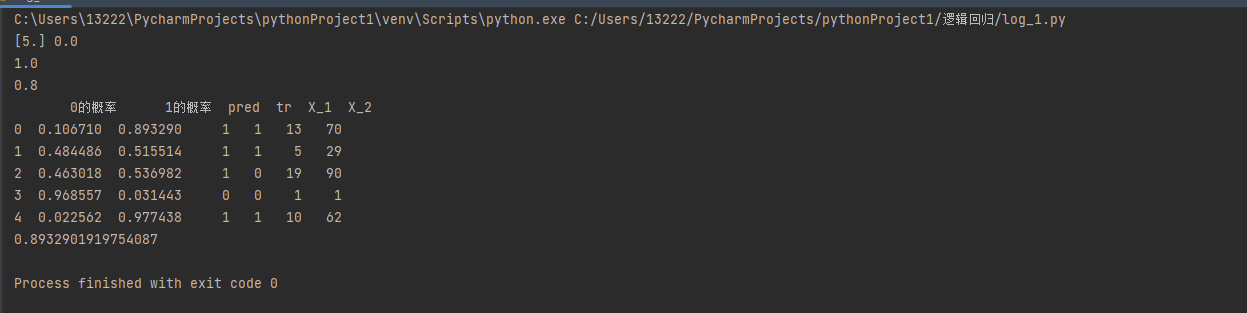
 3.3 代码展示

import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
import warnings
warnings.filterwarnings('ignore')

df = pd.read_excel(io='../data/逻辑回归.xlsx',sheet_name='Sheet1')

X1 = df.drop(columns=['Y_1', 'X_2', 'Y_3'])
X2 = df.drop(columns=['Y_1', 'Y_3'])
y1 = df['Y_1']
y3 = df['Y_3']


# 测一下线性回归
X_train, X_test, y_train, y_test = train_test_split(X1, y1, test_size=0.25, random_state=2)
lir = LinearRegression()
lir.fit(X_train, y_train)
print(lir.coef_, lir.intercept_)
print(lir.score(X_test, y_test))


# 下面是逻辑回归
X_train, X_test, y_train, y_test = train_test_split(X2, y3, test_size=0.25, random_state=2)
lor = LogisticRegression()
lor.fit(X_train, y_train)
sc = lor.score(X_test,y_test)
print(sc)

# 造一个DataFrame
pro = pd.DataFrame(data=lor.predict_proba(X_test),columns=['0的概率', '1的概率'])
pro['pred'] = lor.predict(X_test)
pro['tr'] = np.array(y_test)
df_X = pd.DataFrame(X_test).reset_index(drop=True)
pro = pd.concat([pro, df_X], axis=1)
print(pro)


# 1的概率是如何算出来的。

def get_pro(x1,x2):
    w1 = lor.coef_[0][0]
    w2 = lor.coef_[0][1]
    w0 = lor.intercept_[0]
    z = w0 + w1*x1+w2*x2
    p = 1/(1+np.exp(-z))
    return p

# 当X_1 = 13 ;X_2 = 70 1的概率为：
print(get_pro(13,70))