4.串

串

1. 串的定义

   串，即字符串是由字符组成的序列。记为
   S='a[1]a[2]...a[n]'(n>=0)

   eg.

   S="HelloWorld";
   T="iPhone 11 Pro Max"
   

   子串：串中任意个连续字符组成的子序列(请回想高中的集合知识)

   主串：包含子串的串

   序号：字符在主串中的位置(第一次出现的位置)

   子串的位置：子串的第一个字符在主串中的位置

   空串 M='' 空格串 N=' '

   串是一种特殊的线性表，数据元素之间呈线性关系

   串的数据对象限定为字符集，串的增删改查通常以子串为操作对象

2. 串的基本操作

   StrAssign(&T,chars)：赋值操作。把串T赋给chars。

   StrCopy(&T,S)：复制操作。由串S复制得到串T。

   StrEmpty(S)：判断字符串S是否为空。

   StrLength(S)：求串长，返回S的元素个数。

   ClearString(&S)：清空串。

   Destroy(&S)：销毁串并释放存储空间。

   Contact(&T,S1,S2)：串连接。用T返回S1，S2连接成的新串。

   SubString(&Sub,S,pos,len)求子串，用Sub返回从S的第pos个位置长度为len的字符串。

   Index(S,T)：定位操作，返回T在S中第一次出现的位置，若没有则返回0。

   StrCompare(S,T)：比较操作。S>T返回1,S=T返回0，S<T返回-1

串的存储结构

1. 串的顺序存储
   

   静态数组实现（定长顺序存储）

   #define MAXLEN 255		//预定义最大串长度
   typedef struct{
   	char ch[MAXLEN];	//每个分量存储一个字符
   	int length;			//串的实际长度
   }SString;
   

   动态数组实现（动态分配存储）

   typedef struct{
   	char *ch;
   	int length;
   }HString;
   HString S;
   S.ch=(char *)malloc(MAXLEN *sizeof(char));
   s.length=0;
   

   可以结合顺序表来理解这部分内容

2. 串的链式存储
   

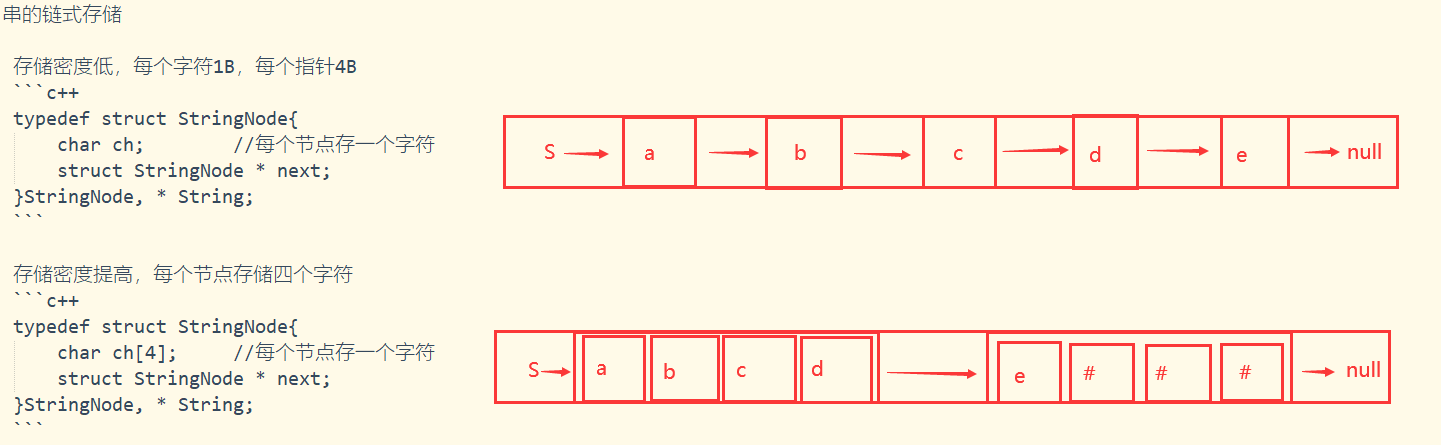
   存储密度低，每个字符1B，每个指针4B

   typedef struct StringNode{
   	char ch;		//每个节点存一个字符
   	struct StringNode * next;
   }StringNode, * String;
   

   存储密度提高，每个节点存储四个字符

   typedef struct StringNode{
   	char ch[4];		//每个节点存一个字符
   	struct StringNode * next;
   }StringNode, * String;
   

串的基本操作实现

1. 求子串

   #define MAXLEN 255		//预定义最大串长度
   typedef struct{
   	char ch[MAXLEN];	//每个分量存储一个字符
   	int length;			//串的实际长度
   }SString;
   
   bool SubString(SString &Sub,SString S,int Pos,int len){
   	if(pos+len-1>S.length) return false;	//子串范围越界
   	for(int i=pos;i<pos+len;i++){
   		Sub.ch[i-pos+1]=S.ch[i];
   	}
   	Sub.length=len;
   	return true;
   }
   

2. 比较操作

   int StrCompare(SString S,SString T){
   	for(int i=0;i<=S.length&&S<=T.length;i++){
   		if(S.ch[i]!=T.ch[i]) return S.ch[i]-T.ch[i];
   	}
   	return S.length-T.length;	//扫描之后字符相同，长度大的串更大
   }
   

3. 定位操作

   int Index(SString S,SString T){
   	int i=1,n=S.length,m=T.length;
   	SString sub;
   	while(i<=n-m+1){
   		SubString(sub,S,i,m);
   		if(StrCompare(sub,T)!=0) ++i;
   		else return i;
   	}
   	return 0;
   }
   

串的朴素模式匹配

什么是模式匹配？

主串：S="wangdao"
子串："wang" "ang" "ao"
模式串："gda" "bao"

串的模式匹配：在主串中找到与模式串相同的子串，并返回其所在的位置

模式匹配本质就是定位操作

1. 朴素模式匹配算法

   int Index(SString S,SString T){
   	int i=j=k=1;
   	while(i<=S.length&&j<=T.length){
   		if(S.ch[i]==T.ch[i]){
   			++i;
   			++j;
   		}else{
   			k++;
   			i=k;
   			j=1;
   		}		
   	}
   	if(j>T.length) return k;
   	else return 0;
   }
   

   另一种方法

   int Index(SString S,SString T){
   	int i=j=1;
   	while(i<=S.length&&j<=T.length){
   		if(S.ch[i]==T.ch[i]){
   			//继续比较后续字符
   			++i;
   			++j;
   		}else{
   			//指针后移重新开始匹配
   			i=i-j+2;
   			j=1;
   		}
   	}
   	if(j>T.length) return i-T.length;
   	else return 0;
   }
   

2. 朴素模式匹配算法的性能分析

   较好的情况：每个子串的第一个字符就与模式串不匹配
   

   最坏的情况：模式串的前几个总能对应上，最后一个对应不上
   

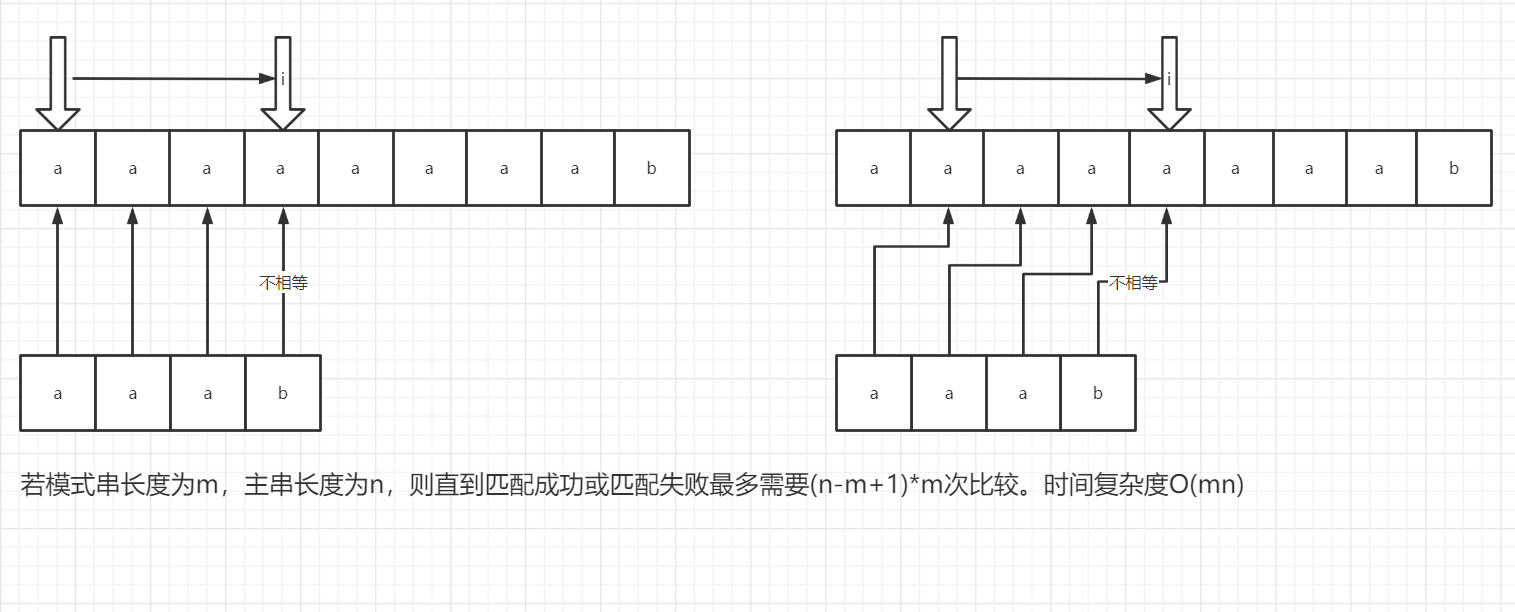
3. KMP算法：朴素模式匹配算法的优化
   

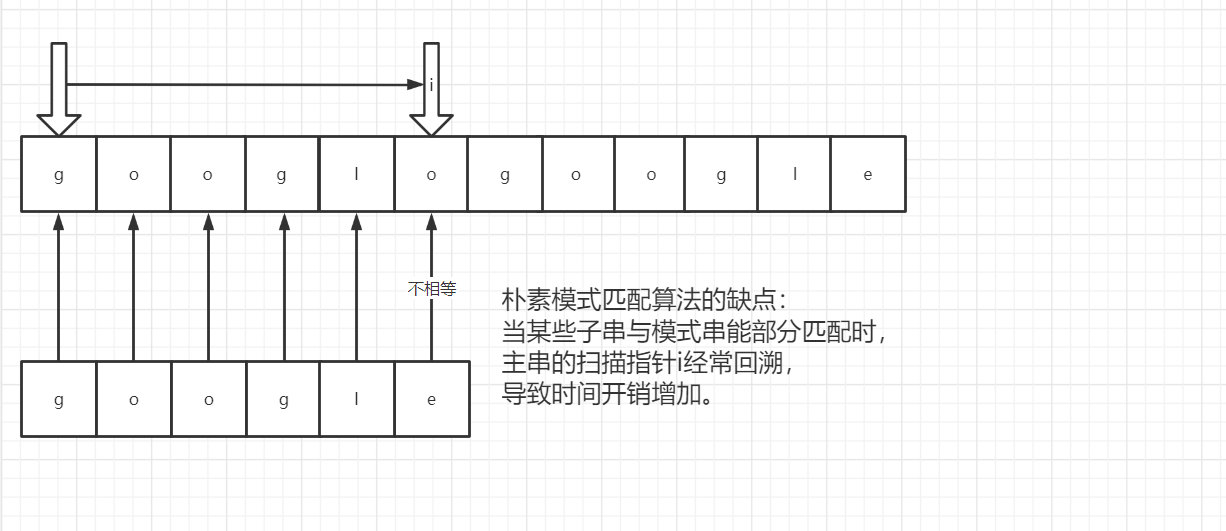
   解决主串回溯问题

   这里很难用文字和图片表述，所以给出：视频链接

   改进思路：主串不回溯指针，只有模式串回溯指针

   若j=k时才发现匹配失败，说明1~k-1都匹配成功

   SString S="googlogooglegooglo";
   SString T="google";
   int next[7]={0,1,1,1,2,1};
   
   int Index_KMP(SString S,SString T){
   	int i=j=1;
   	while(i<=S.length&&j<=T.length){
   		if(j==0||S.ch[i]==T.ch[i]){
   			++i;
   			++j;
   		}else j=next[j];
   	}
   	if(j>T.length) return i-T.length;
   	else return 0;
   }
   

   求模式串的next数组

   这里很难用文字和图片表述，所以给出：视频链接

   next数组：当模式串的第j个字符匹配失败时，领模式串调到next[j]再继续匹配

   Eg.

   #define MAXLEN 255		//预定义最大串长度
   typedef struct{
   	char ch[MAXLEN];	//每个分量存储一个字符
   	int length;			//串的实际长度
   }SString;
   
   SString T='abcabd';
   SString S='abcab????';//当j=6时匹配失败
   //--->
   next[6]=3
   
   SString S='?????????';//当j=1时匹配失败
   //--->
   next[1]=0;//无论什么模式串，next[1]=0是确定的
   
   //======
   
   SString T='abababcdef';
   SString S='ababab?????????';//当j=7时匹配失败
   //--->
   next[7]=5;
   
   //======
   
   SString T='aaaabcd';
   SString S='aaaa??????';当j=5时匹配失败
   //--->
   next[5]=2;
   
   //======
   
   SString T='abcdefg';
   SString S='abcd?????';当j=5时匹配失败
   //--->
   next[5]=1;
   

   串的前缀：包含第一个字符，且不包含最后一个字符的子串

   串的后缀：包含最后一个字符，且不包含第一个字符的子串

   前缀后缀的概念与英语单词的前缀后缀概念是一样的

   当第j个字符匹配失败时，有前1~j-1个字符组成的串记为S,则：
   next[j]=S的最长相等前后缀长度+1
   特殊情况，next[1]始终等于0，next[2]始终等于1

   模式串：'ababaa'

   序号j	1	2	3	4	5	6
   模式串	a	b	a	b	a	a
   next[j]	0	1	1	2	3	4

   

   next[j]={
   	0, j=1
   	max{k|1<k<j&&'p[1]...p[k-1]'=='p[j-k+1]...p[j-1]'}
   	1, 其他情况
   }
   

4. KMP算法机算实现
   

   //求模式串T的next数组
   void get_next(SString T,int next[]){
   	int i=1,j=0;
   	next[1]=0;
   	while(i<T.length){
   		if(j==0||T.ch[i]==T.ch[j]){
   			++i;
   			++j;
   			next[i]=j;
   		}else j=next[j];
   	}
   }
   
   //KMP算法
   int Index_KMP(SString S,SString T){
   	int i=j=1;
   	int next[T.length+1];
   	get_next(T,next);
   	while(i<=S.length&&j<=T.length){
   		if(j==0||S.ch[i]==T.ch[i]){
   			++i;
   			++j;
   		}else j=next[j];
   	}
   	if(j>T.length) return i-T.length;
   	else return 0;
   }
   

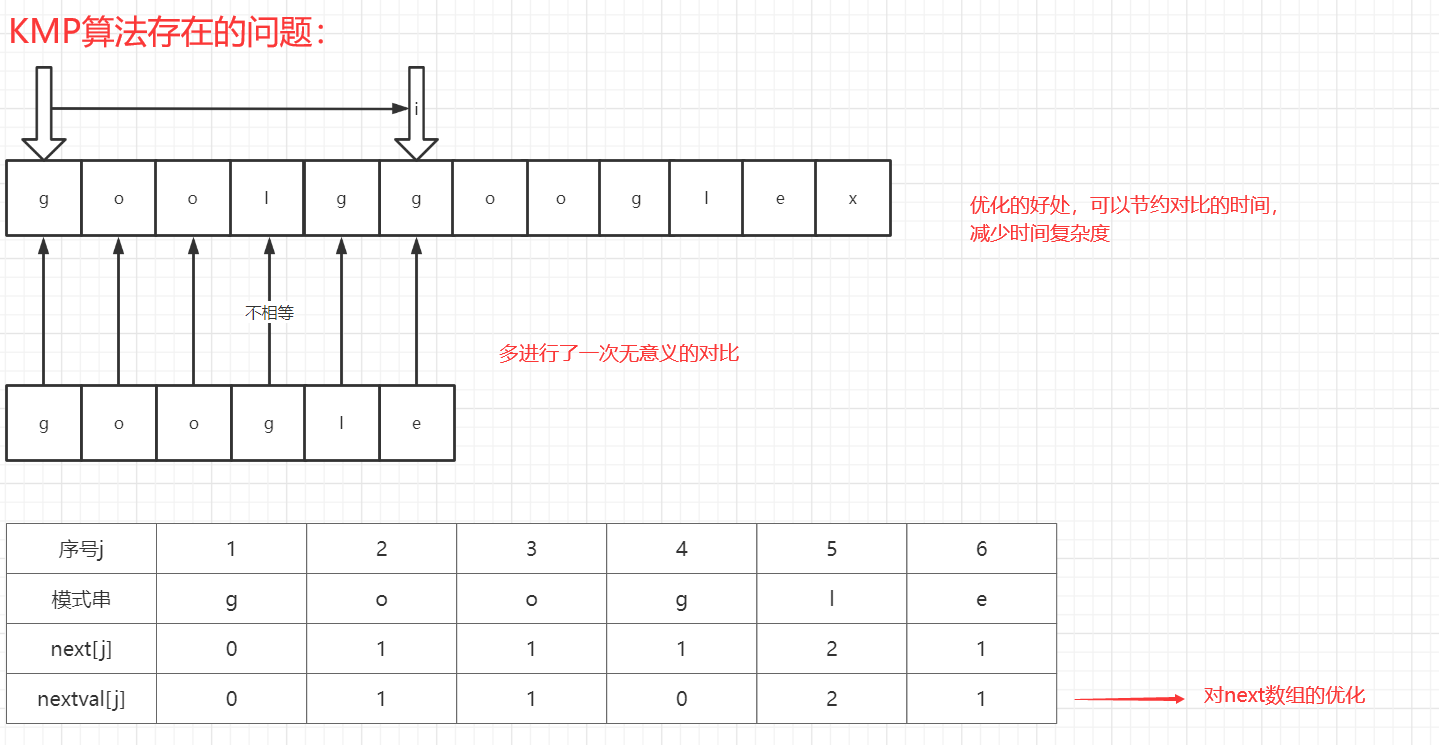
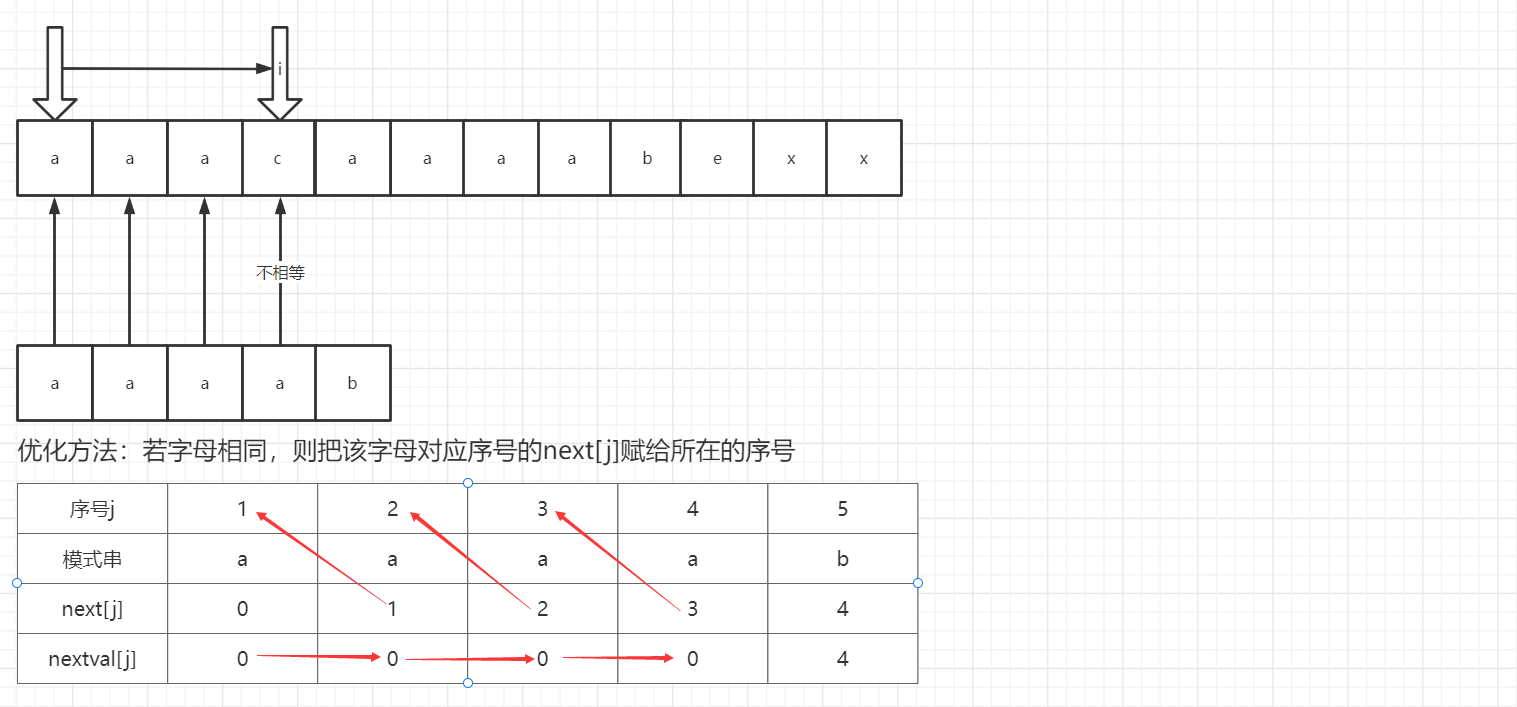
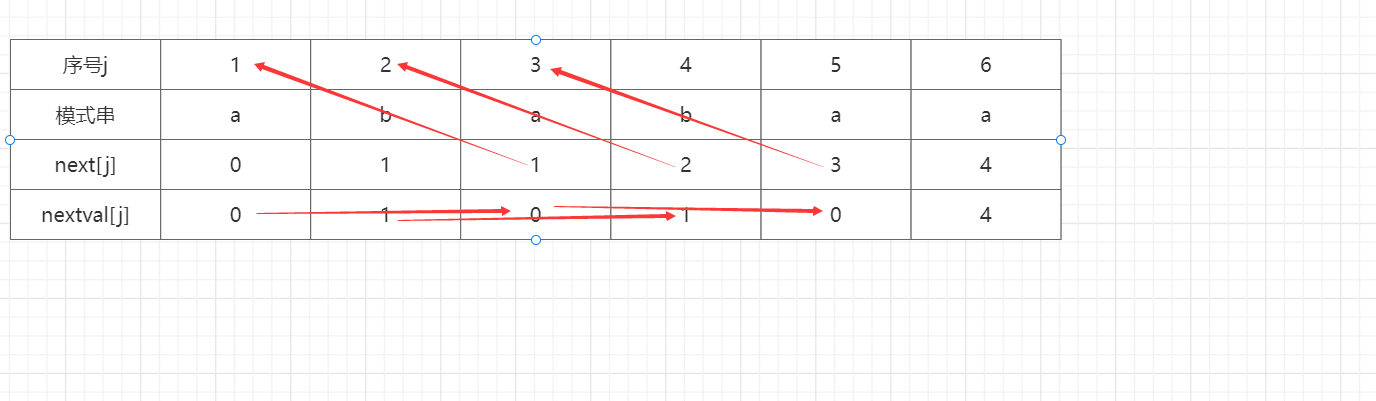
5. KMP算法优化---nextval数组