GIOU 相比于IOU的好处

前言：

　　在目标检测的任务中，一样的损失函数可能有不同的IOU值，如下图（L2作为损失函数）

 

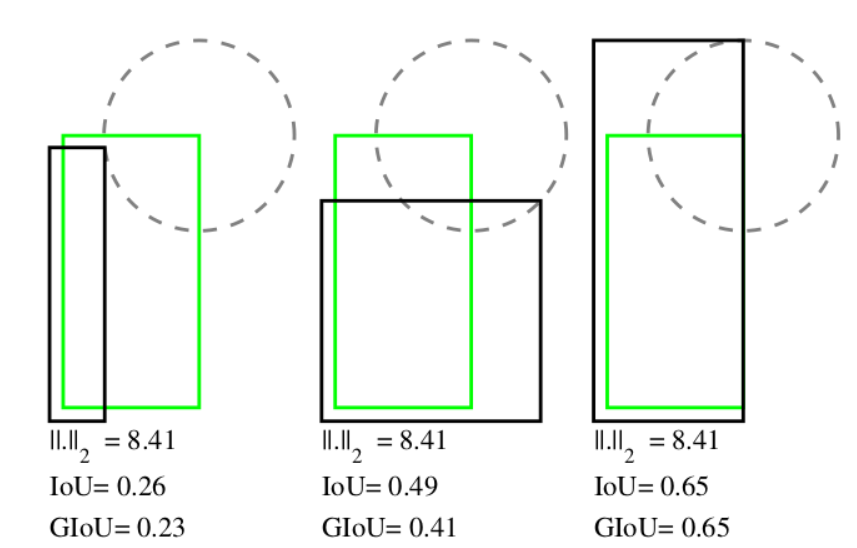
　　上图三张图有一样的L2距离，但是IoU值却完全不同。坐标表示方法为(x1,y1,x2,y2)。

　　下图为L1距离。坐标表示方法为(x,y,w,h)，x,y为中心点坐标。

 

 

 科普一下L1与L2距离，明白的请跳过：

 

 

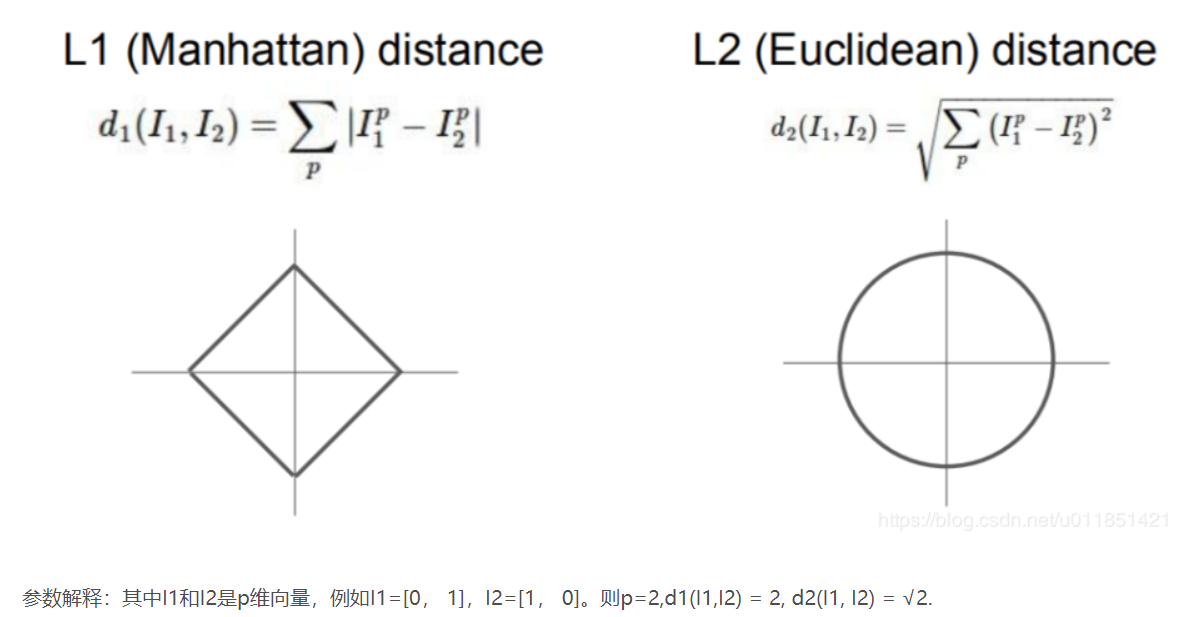
 IOU有它的优点也有它的缺点：

优点：

　　IOU作为距离时(比如：作为损失函数时L=1−IOU)，是一个度量。它包含了作为度量的非负性，不确定性对称性和三角不等性等所有属性。

IoU有尺度不变性，也就是说任意两个方框Ａ和Ｂ的相似性与他们的空间尺度大小无关。
缺点:
　　1.如果两个目标没有重叠，IoU将会为０,此时两个方框距离无论远近，IOU都无法体现，如果IoU用作于损失函数，梯度为０，无法优化。
　　2.IoU无法区分两个对象之间不同的对齐方式。更确切地讲，不同方向上有相同交叉级别的两个重叠对象的IoU会完全相等。如下图

 

 

于是GIOU应运而生：

　　对于任意的Ａ、B框，首先找到一个能够包住它们的最小方框Ｃ。然后计算C \ (A ∪ B) 的面积与Ｃ的面积的比值，注：C \ (A ∪ B) 的面积为C的面积减去A∪B的面积。再用Ａ、Ｂ的IoU值减去这个比值得到GIoU。

 

 

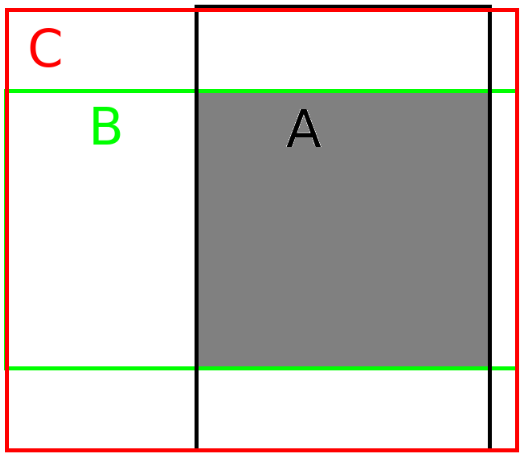
GIoU作为度量时的性能：GIoU作为距离时，L=1−GIoU，具有非负性，不确定性，对称性以及三角不等性，尺度不变性。

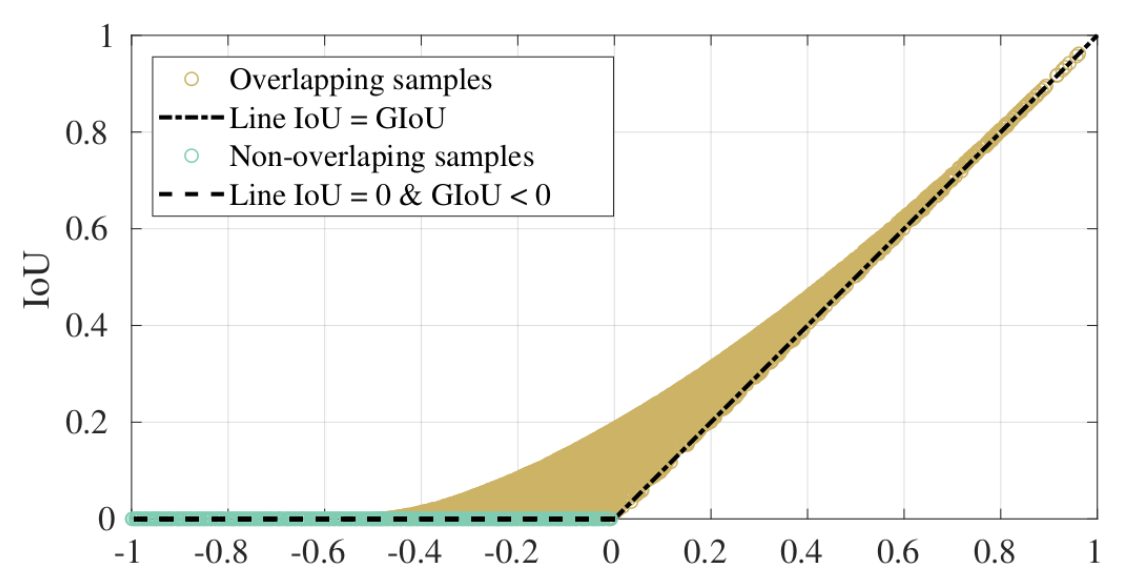
GIoU始终是IoU的下限，即GIoU(A,B) <= IoU(A,B)。当A,B形状相似，并且接近时，GIoU(A,B)接近=IoU(A,B)

其范围是-1 ≤ GIoU(A,B) ≤ 1。A,B完全重合时，GIoU(A,B) = IoU(A,B) = 1。(A∪B)/C→0 时，也就是A∪B的面积相对于C框很小很小时，GIoU收敛于-1。
GIoU考虑到了 IoU 没有考虑到的非重叠区域，能够反应出 A,B 重叠的方式。

IoU和GIoU做为边框损失函数时的算法流程：

 

 

 

————————————————————————————————————————

本文基于CSDN博主「景唯acr」的博文进行了知识扩展以及增删操作
原文链接：https://blog.csdn.net/weixin_41735859/article/details/89288493