Unleashing the Power of Imbalanced Modality Information for Multi-modal Knowledge Graph Completion学习心得

摘要

  多模态知识图补全（MMKGC）旨在通过将实体的结构、视觉和文本信息整合到判别模型中，预测多模态知识图谱中缺失的三元组。现有的MMKGC方法忽略了实体之间模态信息的不平衡问题，导致模态融合不足，原始模态信息的利用效率低下。为了解决上述问题，作者提出了自适应多模态融合和模态对抗训练（AdaMF-MAT），以释放MMKGC不平衡模态信息的力量。AdaMF-MAT通过自适应模态权重实现多模态融合，并通过模态对抗训练进一步生成对抗样本，以增强不平衡的模态信息。

引言

  知识图谱三元组，就不赘述了。多模态KG，包括图片、文字等多模态信息。KG往往完整，需要补全。主流的KGC方法采用知识图嵌入（KGE）对KGs中的结构信息进行建模，将实体和关系嵌入到低维连续空间中。
  然而，现有的方法忽略了实体之间模态信息的不平衡，这可以从两个角度观察到。首先，对于知识图推理，不同的模态信息起着不同的作用，应该自适应地考虑。然而，现有的方法没有充分解决模态融合问题，因为模态信息往往被僵化地统一纳入结构信息的表示空间。其次，图像和文本描述中的有效特征通常是有限的，难以提取。在实际场景中，由多个异构数据源构建的KG甚至存在模态缺失，进一步限制了MMKGC中模态信息的利用。
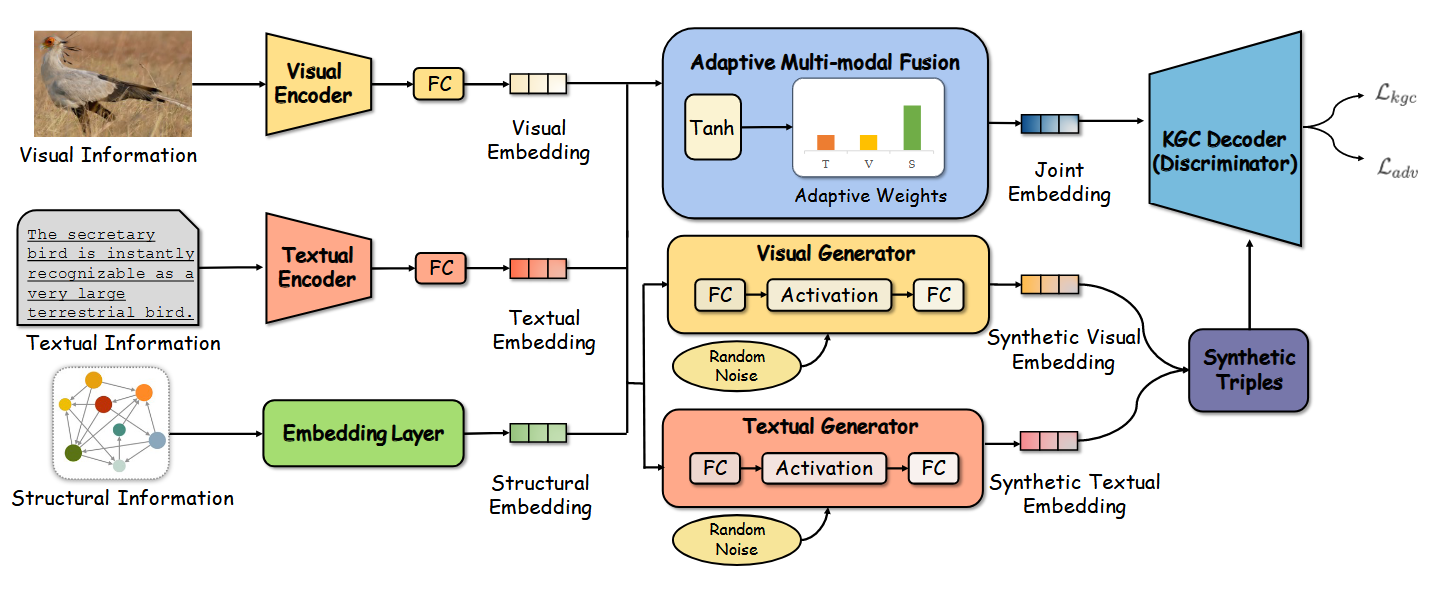
  为了解决这个问题，作者提出了一种新的MMKGC框架，该框架具有自适应多模态融合和模态对抗训练（AdaMFMAT），可以增强和有效利用多模态信息。作者介绍了AdaMF，这是一个自适应多模态融合（AdaMF）模块，它从实体中选择性地提取基本的多模态特征，以生成具有代表性的联合嵌入。作者进一步提出了一种模态对抗训练（MAT）策略，用于生成合成多模态嵌入并构建对抗示例，旨在增强训练过程中有限的多模态信息。虽然现有的负采样方法设计了复杂的策略来在给定的KG中采样，但我们的方法直接创建了具有语义丰富的多模态信息的合成样本，以增强多模态嵌入学习。作者贡献主要有三方面：

1. 提出了用于MMKGC的自适应多模态融合（AdaMF），以融合三种模态（结构、视觉和文本）的不平衡模态信息，并生成具有代表性的联合嵌入。
2. 提出了一种模态对抗训练策略（MAT）来利用不平衡的模态信息。MAT旨在通过合成多模态嵌入生成对抗性示例，从而增强MMKGC训练。
3. 对三个公共基准进行了全面的实验和进一步的探索，以评估AdaMFMAT的性能。

方法论

预备知识

  知识图谱(KG)一般被表示为\(\mathcal{G}=\mathcal{(E,R,T)}\),\(\mathcal{E,R}\)是实体集，\(\mathcal{T = \{(h, r, t)∣h, t \in E, r \in R}\}\)是三元组集合，对于多模态KG（MMKG），每个实体\(e \in \mathcal{E}\)，拥有图像集\(\mathcal{V}_e\)和相关的文本表述。
  MMKGC模型将实体和关系嵌入到连续向量空间中。对于每个实体\(e_i \in \mathcal{E}\),我们将其结构/视觉/文本嵌入分别定义为\(e_s,e_v,e_t\)以表示其不同的模态特征。对于每个关系\(r \in \mathcal{R}\)，我们将其结构嵌入表示为\(r\),此外，MMKGC模型可以用分数函数\(\mathcal{F}\)来衡量每个三元组\((h,r,t)\in \mathcal{T}\),分数函数\(\mathcal{F}\)可以通过定义的嵌入来计算。在KGC任务的推理阶段，对于给定的查询\((h,r,?)\)或\((?,r,t)\)，模型对每个候选实体的相应的三元组得分进行排名并进行预测。

多模态特征编码

  这一节首先介绍了从原始图像和实体的文本描述中提取多模态特征的编码过程。这是所有MMKGC方法的必要步骤。
  对于视觉模态，作者首先使用预训练视觉编码器(PVE)，对每个实体\(e\)先提取出视觉特征\(f_v\),然后通过平均池化和映射把特征投射到嵌入空间中，可以表示为：

$f_v=\frac{1}{|\mathcal{V_e}|} \sum_{img_i \in \mathcal{v_e}}PVE(img_i) \ (1)$ $e_v=W_v \cdot f_v + b_v \ (2)$   此处$W_v$，$b_v$是视觉映射层的参数。

  对于文本嵌入，我们类似地提取每个实体的文本特征及其描述和预训练的文本编码器(PTE)，特殊的[CLS]标记用于捕获句子级文本特征\(f_t\)，这是一种常见的技术。然后，将文本特征\(f_t\)投影到嵌入空间，并使用\(W_t\)和\(b_t\)参数化的另一个映射层在获得文本嵌入\(e_t\)，可以表示为:

$e_t=W_t\cdot f_t + b_t \ (3)$

自适应多模态融合

  在MMKGC中，应仔细考虑三种模态\(m \in \mathcal{M=\{s,v,t\}}\)去衡量三元组的似然性。现有的方法处理方式过于简单，于是作者提出了自适应多模态融合（简称AdaMF）机制来实现自适应模态融合。对于实体\(e\)和对应的嵌入\(e_m\)，其中\(m \in \mathcal{M}\)，AdaMF的工作方式如下：

$\alpha_m=\frac{exp(w_m \oplus tanh(e_m))}{\sum_{n \in \mathcal{M}}exp(w_n \oplus tanh(e_n))} \ (4)$ $e_{joint}=\sum_{m \in \mathcal{M}} \alpha_me_m \ (5)$   $\alpha$是自适应权重，$\oplus$是逐点乘积操作，$w_m$是模态$m$的可学习向量。$e_{joint}$是实体$e$的联合嵌入。通过AdaMF的这种设计，我们可以学习不同实体的不同模态权重，从而实现自适应模态信息融合，产生具有代表性的联合嵌入。

  此外作者使用RotatE模型作为的评分函数来衡量三元组合理性。它可以表示为：

$\mathcal{F(h,r,t)=||h_{joint} \circ r-t_{joint}||} \ (6)$   其中$\circ$是复杂空间中的旋转操作。得分函数中采用了头部和尾部实体的联合嵌入。 $\mathcal{L_{kgc}=\frac{1}{|T|}\sum_{(h,r,t)\in T}\Bigl(-log\sigma(\gamma-F(h,r,t))-\sum_{i=1}^{\mathbf{K}}p_i}log\sigma(\mathcal{F}(h_i^{'},r_i^{'},t_i^{'})-\gamma)\Bigr)\ (7)$   $\sigma$是sigmoid函数，$\gamma$是裕度，$p_i$是负采样生成的每个负三元组$(h_i^{'},r_i^{'},t_i^{'})$的自对抗权重，自对抗权重$p_i$可被表示为： $p_i=\frac{exp(\beta \mathcal{F(h_i^{'},r_i^{'},t_i^{'})})}{\sum^K_{j=1}exp(\beta \mathcal{F(h_j^{'},r_j^{'},t_j^{'})})} \ (8)$   $\beta$是温度参数，我们模型的一个主要训练目标是最小化$\mathcal{L_{kgc}}$。

模态对抗训练

  虽然AdaMF可以自适应地选择多模态嵌入并将其融合为联合嵌入，但它无法增强现有的多模态嵌入以提供更丰富的语义信息。
  作者为MMKGC设计了一种模态对抗训练（MAT）机制，以增强不平衡的多模态信息。MAT采用了一个产生对抗样本的生成器\(G\)和一个测量其合理性的鉴别器\(D\),这遵循了一般对抗训练的范式。

生成器

  作者设计了一个模态对抗生成器(MAG)，它通过生成以结构嵌入\(e_s\)为条件的合成多模态嵌入来承担\(G\)的角色，旨在构建对抗样本。MAG是一个两层前馈网络，可以表示为：

$G_m(e_s,z)=W_2 \cdot \delta(W_1\cdot[e_s;z]+b_1)+b_2 \ (9)$   $W_1,W_2,b_1,b_2$是两个前馈层的参数，$\delta$是LeakyReLU激活函数。$m \in \{v,t\}$是视觉/文本模态，$z $~ $\mathcal{N(0,1)}$是随机噪音。   对于每个三元组$(h,r,t)$，为头部和尾部实体生成合成多模态嵌入，并构建合成实体。合成头部实体$h^{*}$有三个嵌入$h_s,h_v^{*},h_t^{*}$，其中$h_v^{*},h_t^{*}$由MAG的$G_v$和$G_t$产生。尾部实体也是如此。

  此外，我们可以用两个合成实体构造三个合成三元组，对于一个三元组\((h,r,t)\)，它们是\(\mathcal{S}(h,r,t)=\{(h,r,t^{*}),(h^{*},r,t),(h^{*},r,t^{*})\}\)，在实践中通常会生成\(L\)组三元组，\(\mathcal{S}\)将包括\(3L\)个合成三元组。由于生成器包含随机噪声，这些合成三元组彼此不同。

---

算法1：
训练AdaMF-MAT(Adaptive Multi-modal Fusion and Modality Adversarial Training，自适应多模态融合与模态对抗训练)的伪代码

输入：从\(\mathcal{T}\)、实体多模态信息、自适应多模态\(D\)、生成器\(G\)中采样一批训练三元组\(\mathcal{B}\)
输出：通过模态对抗训练的来的多模态知识图谱补全模型

1.for each triple$(h,r,t) \in \mathcal{B}$ do

2.   // Training 自适应多模态融合\(D\)

3.   获取联合嵌入\(h_{joint},t_{joint}\)

4.   计算三元组得分\(\mathcal{F}(h,r,t)\)和负样本三元组得分\(\mathcal{F}(h_i^{'},r_i^{'},t_i^{'})\)。

5.   计算kgc loss\(\mathcal{L_{kgc}}\)

6.   用\(G\)生成对抗性示例集\(S\)。

7.   计算对抗性损失\(\mathcal{L_{adv}}\)

8.   计算总损失\(\mathcal{L_{kgc}}+\lambda\mathcal{L_{adv}}\)

9.   反向传播和优化\(D\).

10.   // Training 生成器\(G\)

11.   获取联合嵌入\(h_{joint},t_{joint}\)

12.   用\(G\)生成对抗性示例集\(S\)。

13.   计算对抗性损失\(\mathcal{L_{adv}}\)

14.   反向传播和优化\(G\)。

15. end

鉴别器

  通过生成具有合成多模态嵌入的对抗性示例，\(D\)旨在区分正（实）三元组和合成三元组，而\(G\)旨在生成真实的三元组并欺骗鉴别器\(D\)。在MMKGC中，我们让得分函数\(\mathcal{F}\)作为对抗训练设置中的\(D\).因为\(\mathcal{F}\)是三元组似性鉴别器，也是对抗性增强的目标。因此，对抗性训练的损失可以设计为：

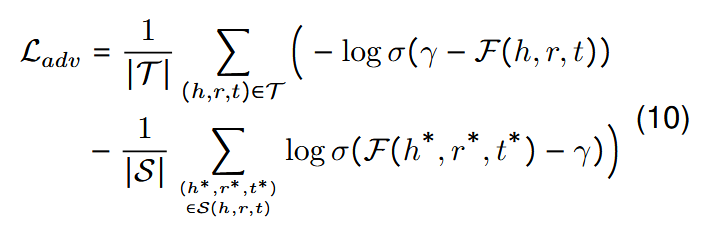
  作者将持损失函数的格式与\(\mathcal{L_{kgc}}\)相似，并对比了正三元组和对抗性示例，因为这种格式更适合MMKGC。从另一个角度来看，模态对抗训练以被视为MMKGC的一种增强的负采样方法，因为我们以对抗的方式生成高质量的反例。模态对抗训练与现有的负采样方法不同的是，模态对抗训练通过对抗训练而不是从现有的KG中采样来生成新的困难负样本。我们的方法引入了具有自适应多模态融合的多模态信息，这是MMKGC模型和训练策略的共同设计。

训练目标

  在训练过程中，我们以对抗的方式迭代训练\(D\)和\(G\)，同时保持优化MMKGC的总体目标\(\mathcal{L_{kgc}}\)，总体培训目标可以表示为：

  其中$\lambda$是对抗损失系数。AdaMF-MAT的小批量训练伪代码如算法1所示。

  在训练过程中，Ada-MF模型D和生成器G将在对抗环境中迭代优化。

实验

  作者在本节主要回答了以下研究问题(RQ):

    RQ1:AdaMFMAT在链路预测任务中的性能与现有的MMKGC方法相比如何(与现有方法的比较，模型的优点)？

    RQ2:AdaMFMAT在模态缺失场景中的表现如何(模型可能存在的短板，模型可能的缺点)？

    RQ3:AdaMF和MAT的设计对性能有多大贡献(新方法的贡献，论文的贡献，消融实验)？

    RQ4：我们能找到一些直观的案例来解释我们方法的性能吗(可解释性)？