2018-2019-20172329 《Java软件结构与数据结构》第五周学习总结
2018-2019-20172329 《Java软件结构与数据结构》第五周学习总结
教材学习内容总结
《Java软件结构与数据结构》第九章-排序与查找
一、查找
- 1、查找概念简述:
(1)查找3是这样一个过程,即在某个项目组中寻找某一指定目标元素,或者确定该组中并不存在该目标元素。对其进行查找的项目组有时也称为查找组。
(2)查找方式的分类:线性查找,二分查找。
(3)查找所要完成的目标:尽可能高效的完成查找,从算法分析的角度而言,我们希望最小化比较操作的次数,通常,查找池里项目数目越多,为了寻找该目标而做出的比较操作次数就越多,因此该查找池中项目的树目定义了该问题的大小。
- 2、线性查找法:
(1)如果该查找池组织成了一个某类型的列表,那么完成该查找的一个简单方式就是从该列表头开始一次比较每一个值,直到找到该目标元素为止。
(2)具体的样式图:

(3)代码实现:
public static <T>
boolean linearSearch(T[] data, int min, int max, T target)
{
int index = min;
boolean found = false;
while (!found && index <= max)
{
found = data[index].equals(target);
index++;
}
return found;
}
- 3、二分查找法:
(1)前提:查找池中的项目组是已排序的。
(2)具体过程:二分查找是从排序列表的中间开始查找,而不是从一端或另一端开始。如果没有在那个中间元素找到目标元素则继续查找。
(3)具体详细的样式图:
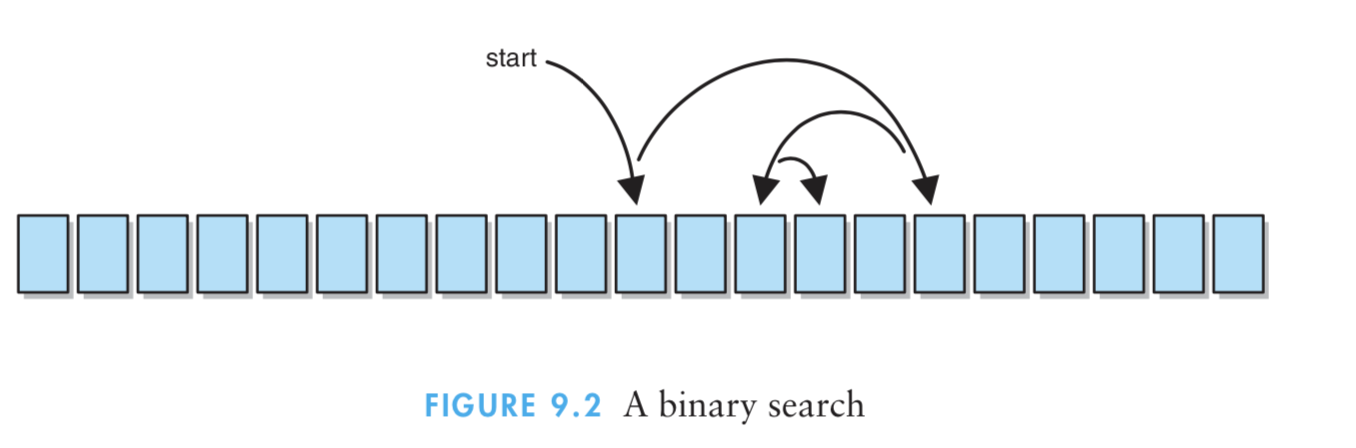
(4)特点:二分查找将利用了查找池是已排序的这一事实;二分查找的每次比较都会删除一半的可行候选项;结合了递归的思想。
(5)代码实现:
public static <T extends Comparable<T>>
boolean binarySearch(T[] data, int min, int max, T target)
{
boolean found = false;
int midpoint = (min + max) / 2; // determine the midpoint
if (data[midpoint].compareTo(target) == 0)
found = true;
else if (data[midpoint].compareTo(target) > 0)
{
if (min <= midpoint - 1)
found = binarySearch(data, min, midpoint - 1, target);
}
else if (midpoint + 1 <= max)
found = binarySearch(data, midpoint + 1, max, target);
return found;
}
(6)注:如果二分查找分为元素为奇数和偶数个两种样式,就具体的问题有具体的解决方式,如果线性表为一个偶数个的有序列表的时候,所采用的中点可以是中间两个值的任意一个。
- 4、查找算法的比较:
(1)对于线性查找而言,最好的情形是目标元素刚好是我们所考察项目组中的第一个项目。
(2)线性查找算法具有线性时间复杂度O(n),因为是依次每回查找一个元素,所以复杂度是线性的——直接与待查找元素数目成比例。
(3)二分查找算法普遍要快得多。最好的情形就是一次比较就找到了该目标——也就是说,目标元素刚好位于数组的中点。最坏的情形出现在元素不在该列表的时候,在这种情形下,在删除所有数据之前,我们不得不进行大约log2n次比较。因此找到位于该查找池中某一元素的预期情形是大约(log2n)/2次比较。
(4)二分查找的复杂度是对数级的,这使得它对于大型查找池非常有效率。
二、排序
- 1、排序概念简述
(1)排序是这样一个过程,即基于某一标准,要么以升序要么以降序将某一组项目按照某个规定顺序排列。
(2)基于效率排序算法分为两类:顺序排序和对数排序。
(3)在顺序排序里,有三种排序方式,分别为:选择排序、插入排序以及冒泡排序。
(4)在对数排序中,有两种排序方式:快速排序和归并排序。
- 2、选择排序法
(1)选择排序算法通过反复地将某一特定值放到它在列表中的最终已排序位置,从而完成对某一列值的排序。
(2)算法实现原理图
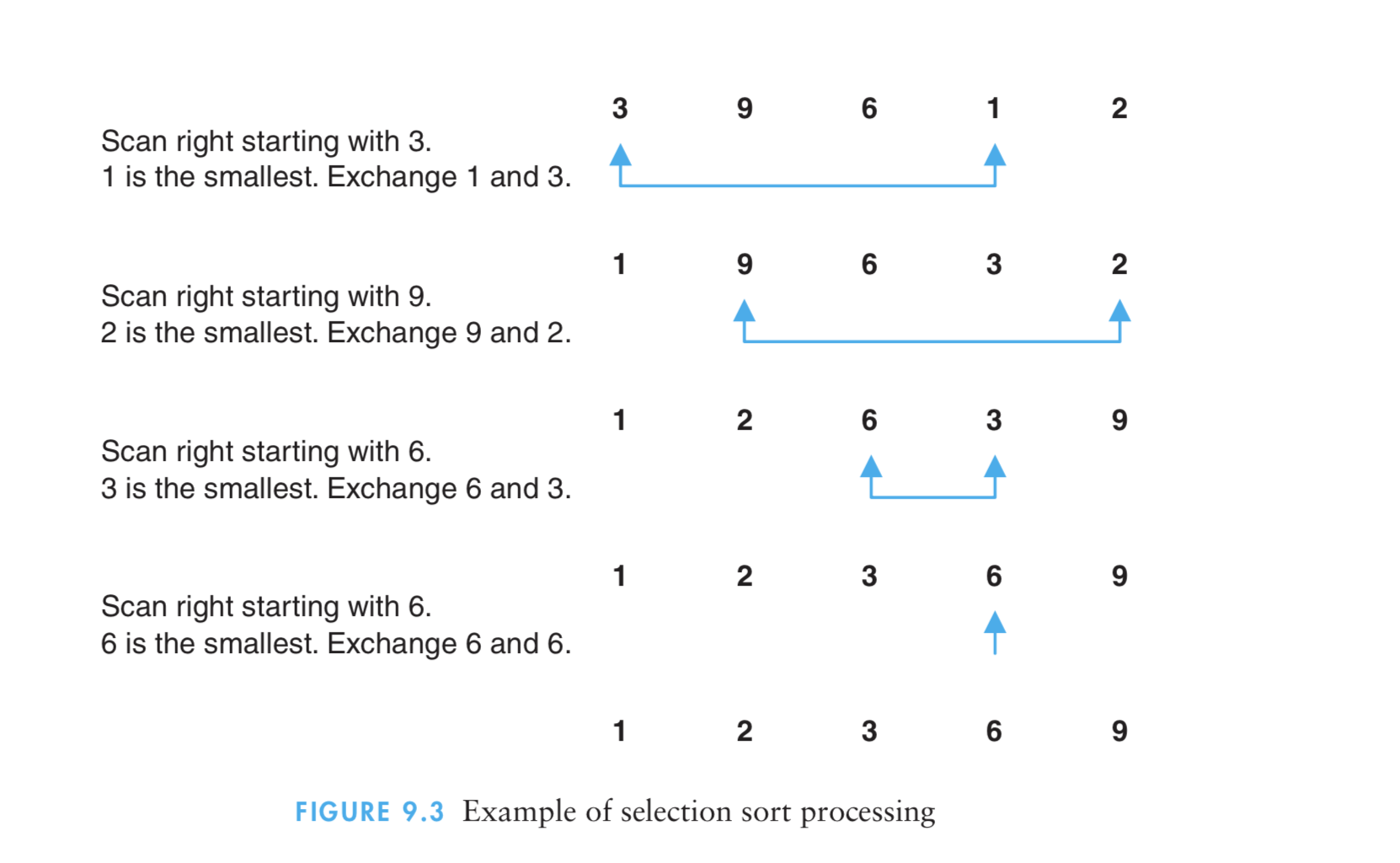
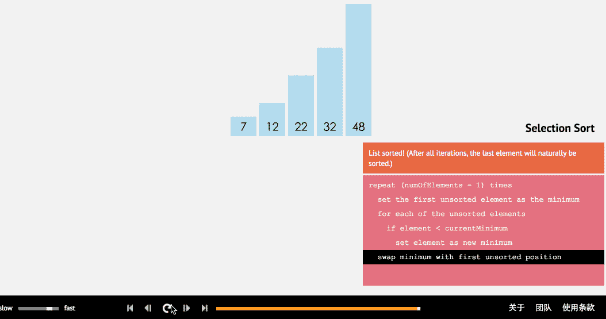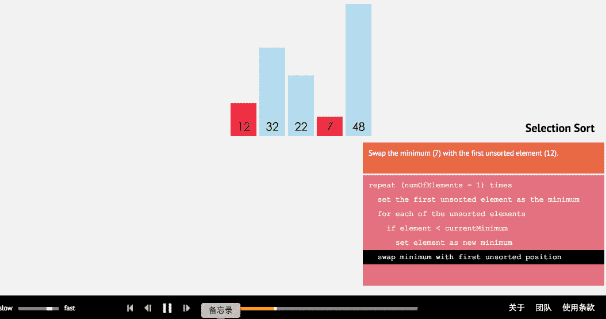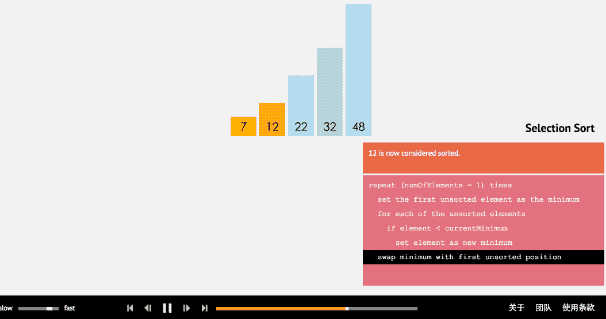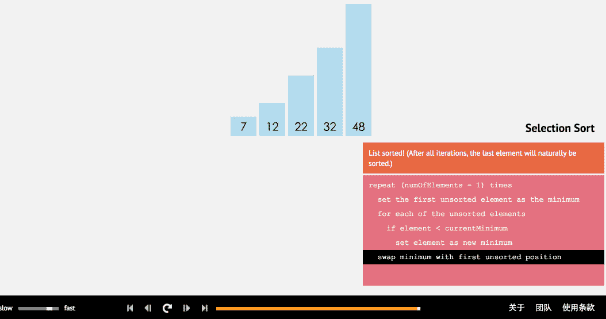
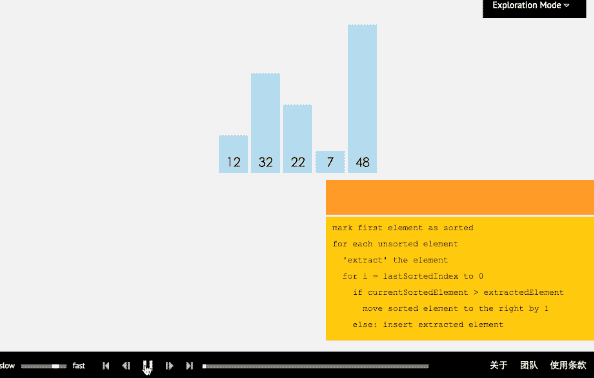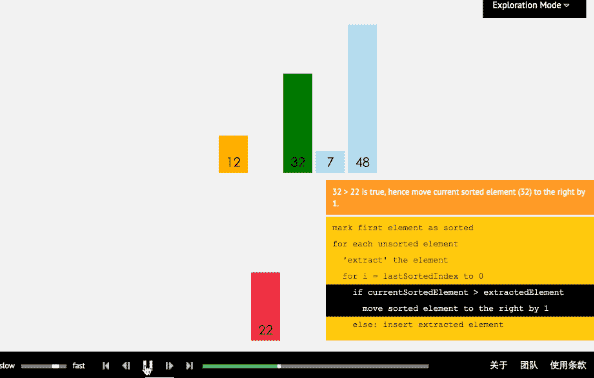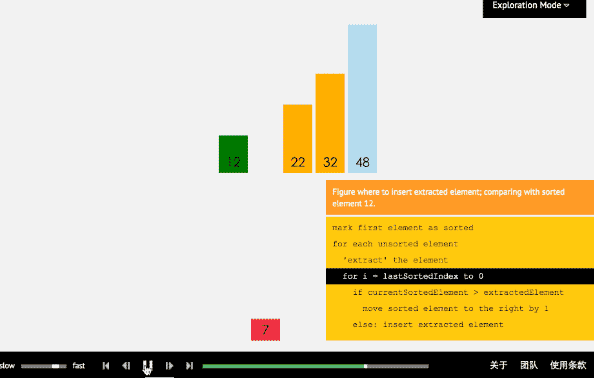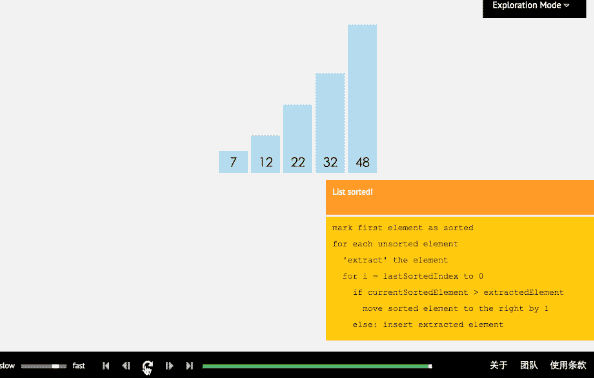
- 3、插入排序法
(1)插入排序算法通过反复地将某一特定值插入到该列某个已排序的子集中来完成对列表值的排序。
(2)算法实现原理图
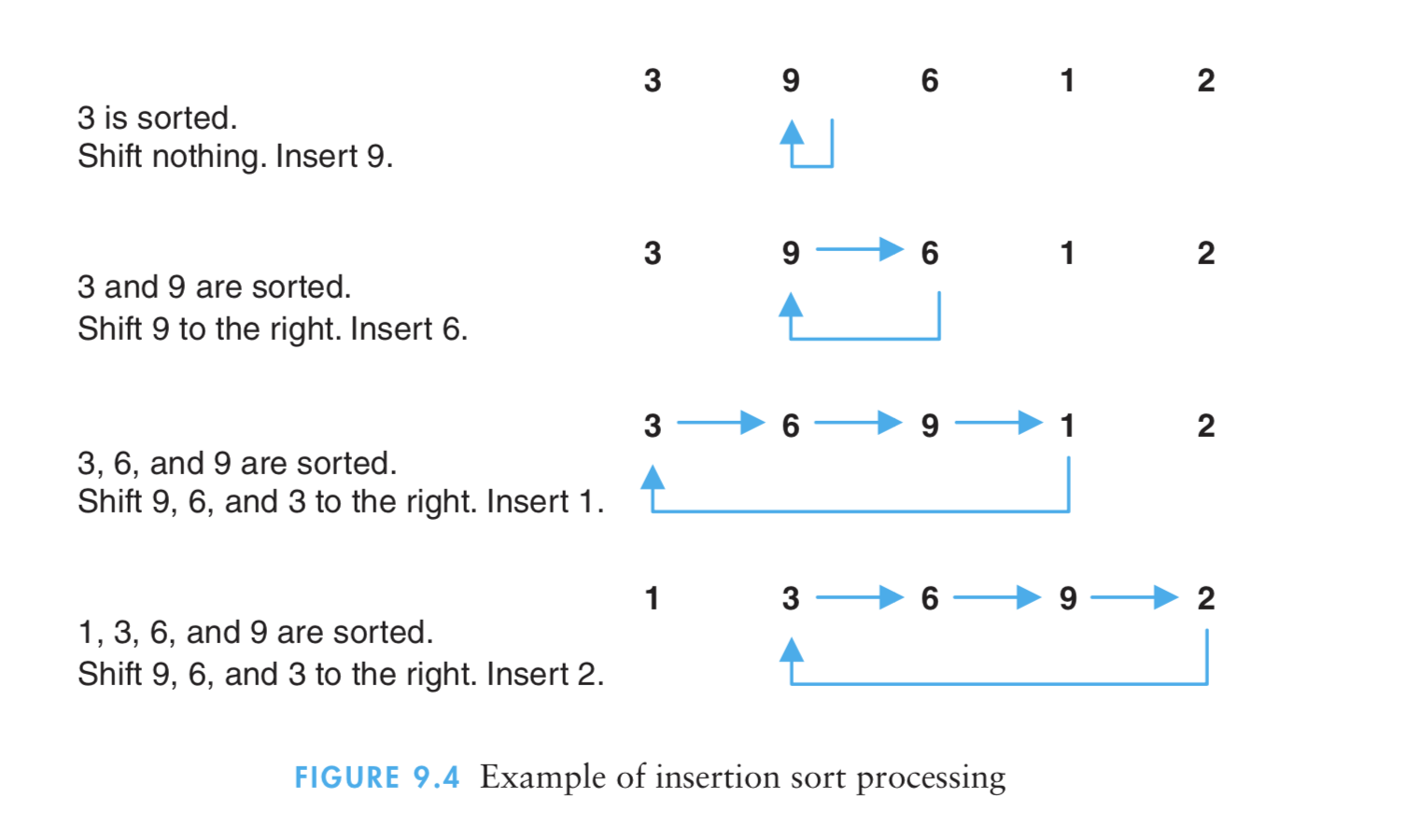
- 4、冒泡排序法
(1)冒泡排序法是另一种使用了两个嵌套循环的顺序排序算法,通过重复地比较相邻元素且在必要时将它们互换,从而完成对某个列表的排序。
(2)算法实现原理图

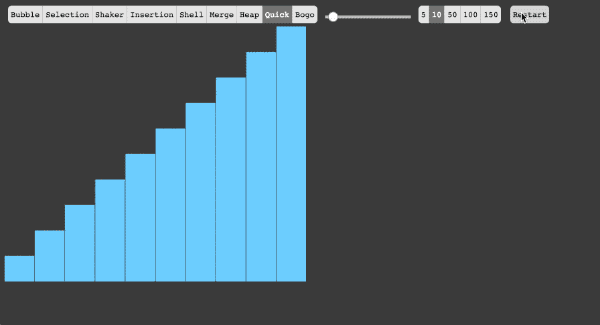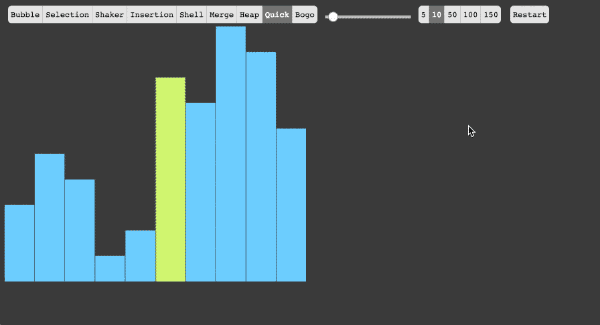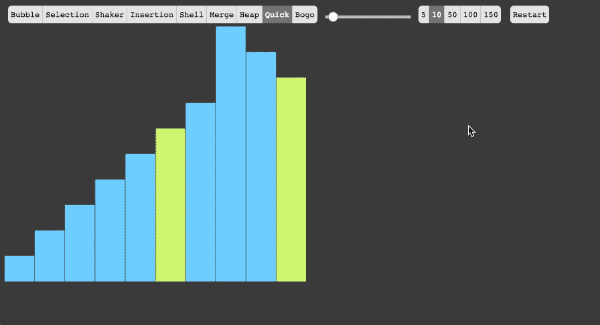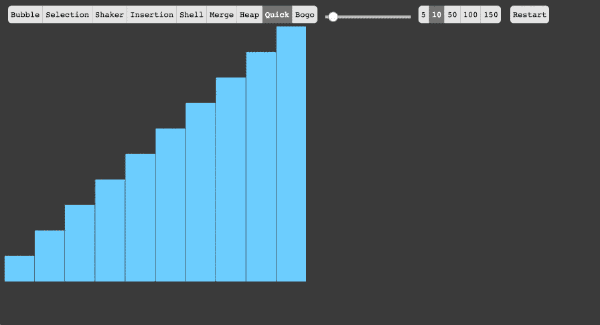
- 5、快速排序法
(1)快速排序算法通过将列表分区,然后对这两个分区进行递归式排序,从而完成对整个列表的排序。
(2)算法实现原理图
- 6、归并排序法
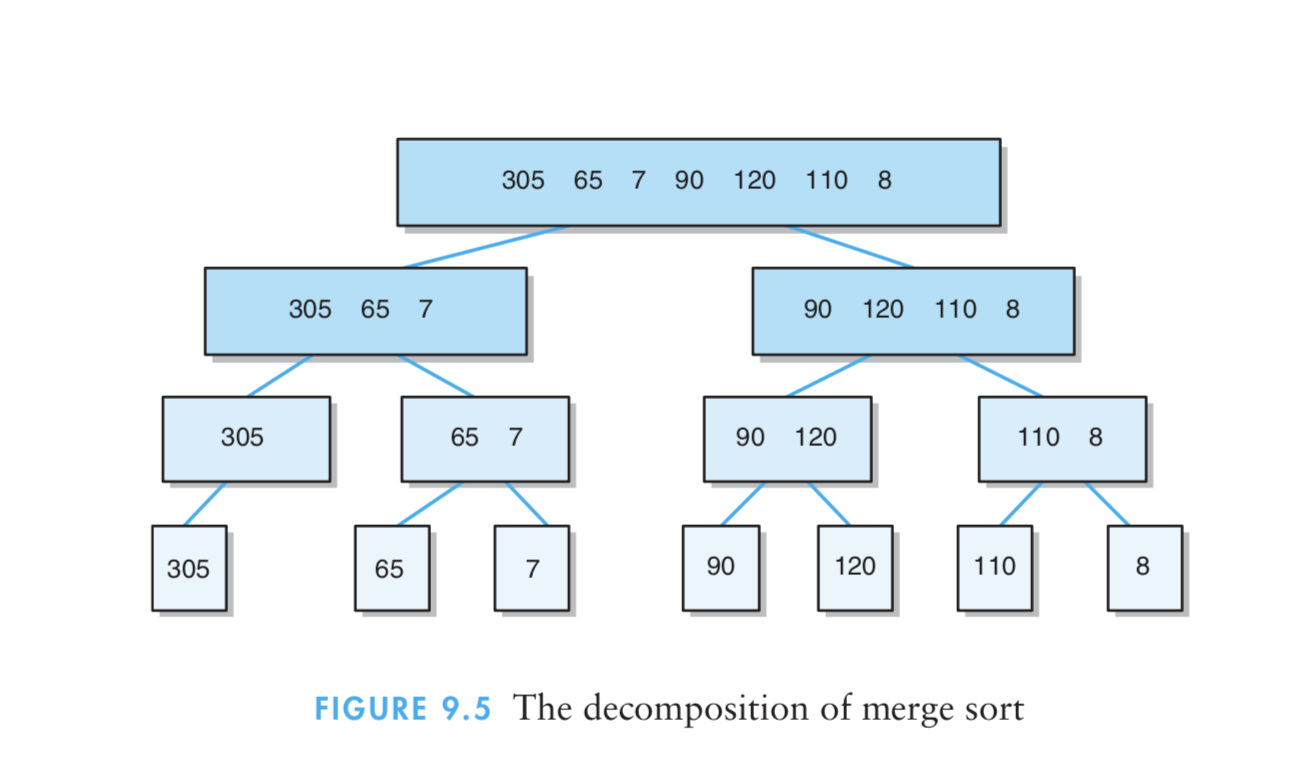
(1)归并排序算法通过将列表递归式分为两半直至每一字列表都含有一个元素,然后将这些字列表归并到一个排序顺序中,从而完成对列表的排序。
(2)算法实现原理图
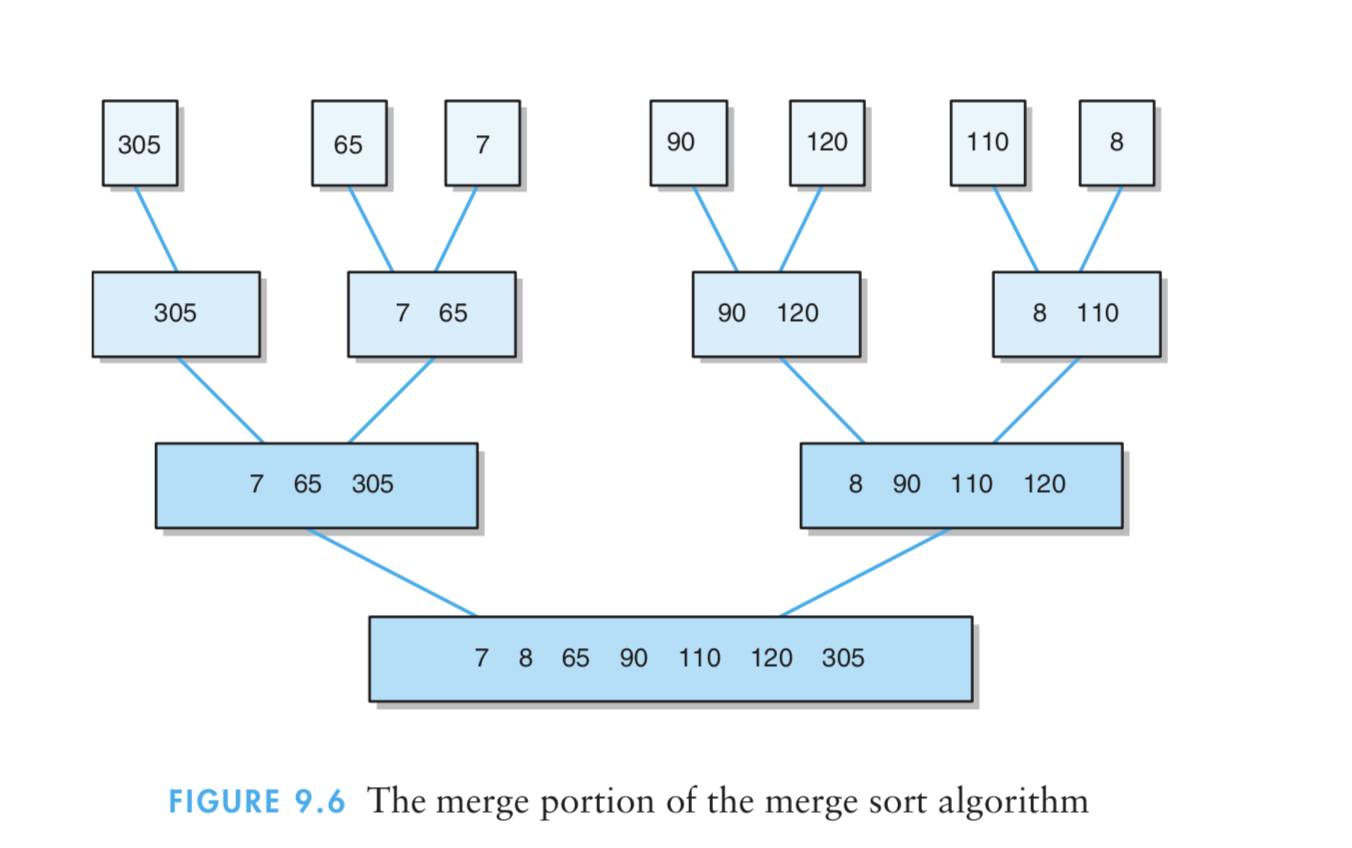

- 7、基数排序法
(1)基数排序是基于队列处理的。
教材学习中的问题和解决过程
- 问题1:在学习到二分查找的时候书中的例子考虑到的是奇数个变量,假如是偶数个变量,我们将如何进行处理?
- 问题1解决过程:包括在老师上课的时候也都讲过,偶数个的话,中间两位任意一个都可以,就这个任意一个都可以就让我有点费解,在看了书中的解释
在二分查找实现中,确定中点索引的计算丢弃了任何分数部分,因此它选择的是两个中间值的第一个。
就这个解释而言,而且当我仅仅看书看到这里的时候,理解起来肯定还是不容易的,所以我继续看了书后面的内容,在看到对数排序的归并排序中,发现其实现的原理非常相似,其中在归并排序的代码实现中,我的问题在其中也有所体现:
int mid = (min + max) / 2;
while (first1 <= last1 && first2 <= last2)
{
if (data[first1].compareTo(data[first2]) < 0)
{
temp[index] = data[first1];
first1++;
}
else
{
temp[index] = data[first2];
first2++;
}
index++;
}
从上述的代码就可以看出,代码实现的过程其实就是分开比较,分类比较,先确定一个数,比它的左边和右边。
-
问题2:在学习选择排序法的过程中,其中在那个
Sorting类中有swap这个写好的方法,其作用就是交换两个数组位置的内容,但是在我们之前学习单链表的时候,在交换节点的时候总是需要考虑各个方面的因素,那我们能不能也写这样一个方法进行结点互换呢? -
问题2解决过程:因为链表中每一个结点都是链接起来的,假如盲目的断掉某一个可能就会导致空指针的问题或者更严重就会导致后面所有数据的丢失,所以在之前学习的过程中,在我学习的过程中,都是用先赋值给一个临时结点,然后把后面的结点插入到前面结点之前,再用后面结点连接到它后面的后面那个结点,这样实现结点的交换,但是这仅仅只能实现于在相邻的两个结点,所以有没有一种方法,我们可以实现类似于
swap的方法呢?所以我首先在网络上寻找有没有讲解类似相关知识的博文以得到灵感。
这是我所找到的一个博主自己画的一张图
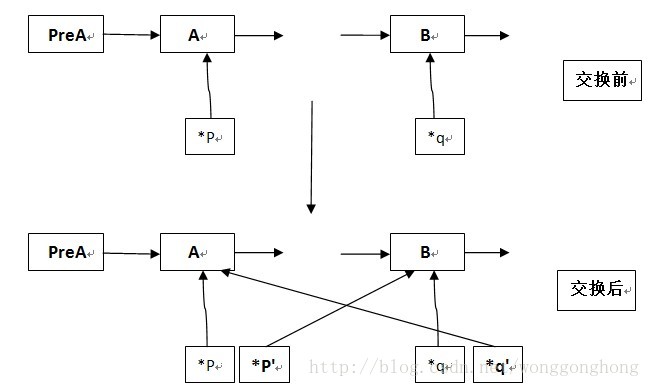
其实回想一下之前自己写过的一个程序中,仿佛自己好像也用到了相关的知识,因为我觉得交换无非就是首先需要找到要交换的元素,再计算它们之间需要进行寻找的次数,也就是它们之间的距离,通过这样几项元素,就可以大致写出伪代码了。
我的伪代码思路就是:(1)因为首先我们需要定义三个形式参数(这里我没有考虑假如交换的元素在链表中出现了多次,这个在接下来的时间里我会再继续解决的),三个形参分别为list node1 node2,其中node1 node2为需要交换的两个元素,首先要找到node1和node2,然后把node1插入到node2的后面,把node2插入到node1的前面,再删除之前的node1和node2。
因为问题提出的时间很短,代码实现正在初步形成中。
-
问题3:在学习快速排序法的时候,有这样一个方法
partition方法,在这个方法中,它最终返回的是一个整型的right,这个类的用处是什么呢? -
问题3解决方法:首先,这个方法的两个内层循环用于寻找位于错误分区的交换元素,第一个循环从左边扫描右边以寻找到大于分区元素的元素,第二个循环,从右边扫描左边以寻找到小于分区元素的元素,在寻找到之后,进行互换。
-
问题4:就上一个问题继续,其中有这样一句代码
int middle = (min + max) / 2;,在上学期中,有学习过在计算机语言中,假如定义一个整型的变量,如果给它赋予一个double型的数字,比如小数,变量最终只取整形的部位,举个例子类似于这样
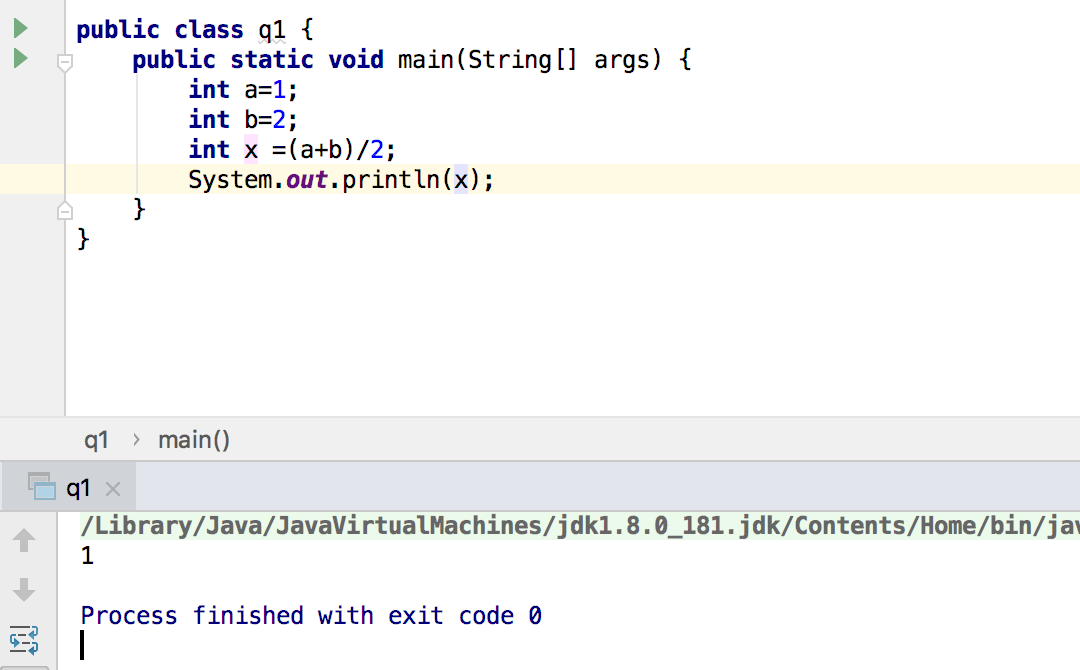
在这个方法中,假如是这个样子,会不会对程序有影响? -
问题4解决方法:这个程序中,有考虑到如此的情况,所以并不会受影响。
代码调试中的问题和解决过程
-
问题1:在做pp9.2的作业中,发现自己所编写的外循环总是走一遍就停下来了,如下:
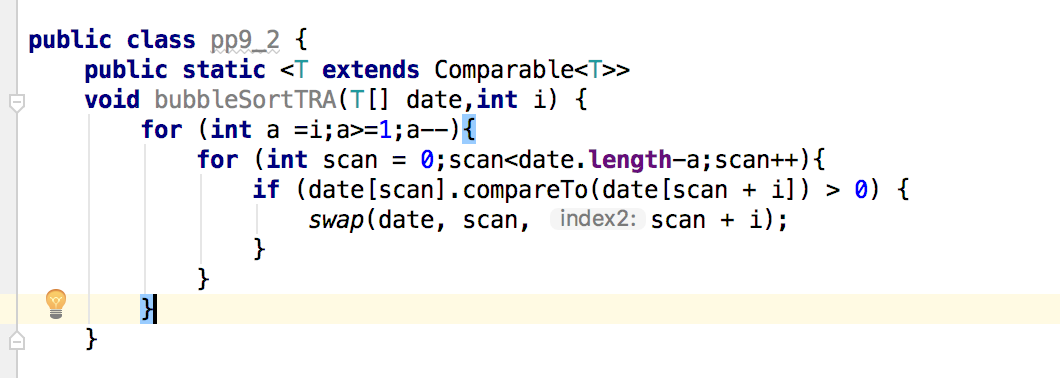
-
问题1解决方法:
一开始以为自己是不是哪里编写错了,就大改了一番,自己重新多写了一个循环,仿照冒泡排序的代码写了一个,错的更厉害了,最后发现自己的错因竟是变量的名称没有修改对。
修改成如下就可以了。
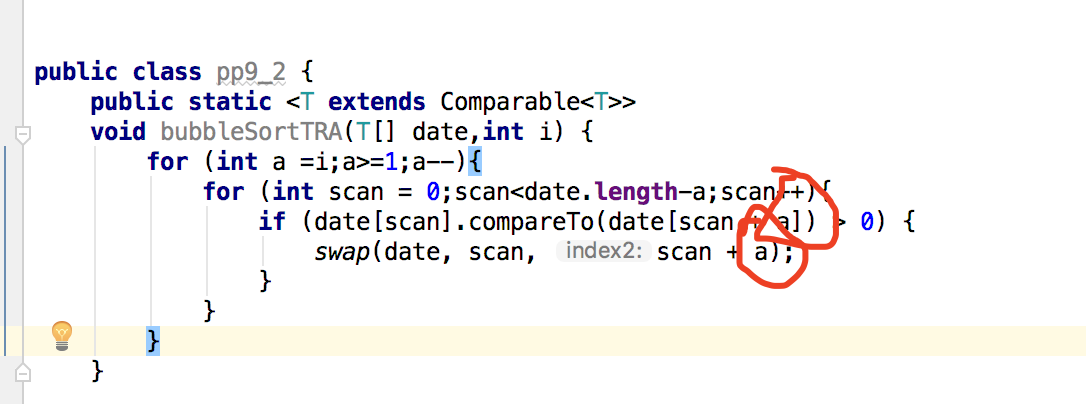
-
问题2:在写pp9.3的时候,再计算时间的时候,发现自己输出的一直是0毫秒?如下图

-
问题2解决方法:因为询问了郭恺同学,在今天也就是十月十四日的时候,郭凯同学说他也遇到了同样的问题,可能是因为毫秒太大使得只显示了实数位,将其改为纳秒的时候,问题也就随之解决了

也就是说,当我们计算毫秒的时候所用的语句是下面代码:
long startTime = System.currentTimeMillis(); //获取开始时间
//doSomething(); 测试的代码段
long endTime = System.currentTimeMillis(); //获取结束时间
System.out.println("程序运行时间:" + (endTime - startTime) + "ms"); //输出程序运行时间
计算纳秒的时候用的计算时间为:
long startTime=System.nanoTime(); //获取开始时间
doSomeThing(); //测试的代码段
long endTime=System.nanoTime(); //获取结束时间
System.out.println("程序运行时间: "+(endTime-startTime)+"ns");
代码链接

上周考试错题总结
上周无错题,太秀了!
结对及互评
- 本周结对学习情况
- 博客中值得学习的或问题:
- 内容详略得当;
- 代码调试环节比较详细;
- 基于评分标准,我给本博客打分:5分。得分情况如下:
-
正确使用Markdown语法(加1分):
-
模板中的要素齐全(加1分)
-
教材学习中的问题和解决过程, 一个问题加1分
-
代码调试中的问题和解决过程, 一个问题加1分
- 博客中值得学习的或问题:
- 内容详略得当;
- 代码调试环节比较详细;
- 基于评分标准,我给本博客打分:9分。得分情况如下:
- 正确使用Markdown语法(加1分):
- 模板中的要素齐全(加1分)
- 教材学习中的问题和解决过程, 一个问题加1分
- 代码调试中的问题和解决过程, 一个问题加1分
感悟
这周上了三节Java课,也发现了自己在学习当中的一些问题,希望自己可以把握住现在可以学习的机会,不要在以后后悔莫及的时候反思自己没有在正确的时间做正确的事情。加油!
不忘初心,方得始终!
学习进度条
| | 代码行数(新增/累积)| 博客量(新增/累积)|学习时间(新增/累积)
| -------- | :----------------😐:----------------😐:---------------: |:-----:
| 目标 | 5000行 | 30篇 | 400小时
| 第一周 | 0/0 | 1/1 | 6/6
|第二周 | 1313/1313 |1/2 | 20/26
|第三周 | 901/2214 | 1/3 | 20/46
|第四周 | 3635/5849| 2/4 | 20/66
|第五周 | 1525/7374 | 1/5 | 20/86
参考资料
蓝墨云班课
Java程序设计
Java计算程序代码执行时间的方法小结
Java实现-两两交换链表中的节点
Java数据结构和算法(九)——高级排序
数据结构常见的八大排序算法

