第一单元总结
第一单元总结
前言
第一单元的三次作业都围绕着表达式展开进行,让我们从面向过程逐渐转变为面向对象。我的主要思路是先进行大量的字符串替换,将字符串替换为仅含有+,-,*三种运算符的式子,再进行表达式的展开。但这种方法的弊端在于不能很好地体现面向对象的思想,替换步骤还是围绕着面向过程来进行的。
一、程序结构分析
1.第一次作业
1.1类图与设计思路
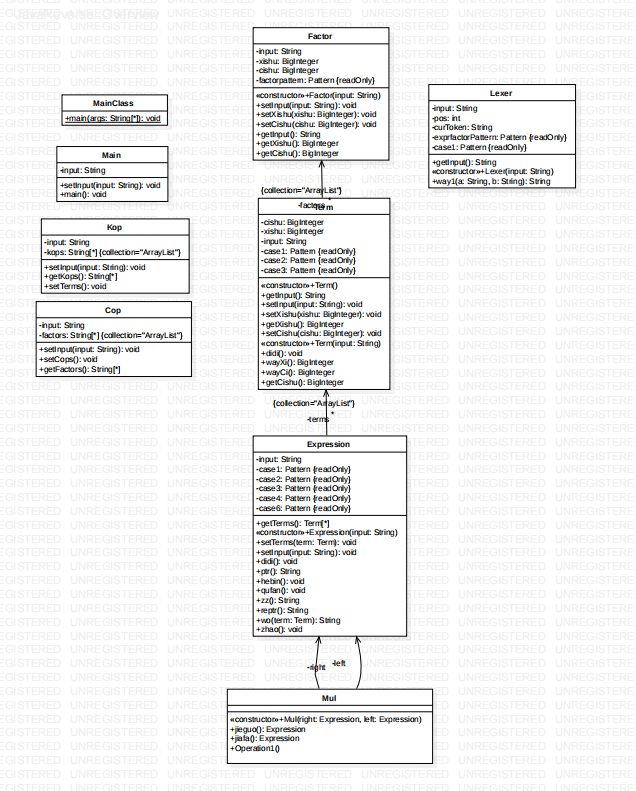
我第一次作业的思路是,字符串处理,解析表达式,简化输出。由于训练中的lexer类没看懂,在我第一次的作业中这个类表示字符串的处理。具体表现为将**替换为^,并且将所有的带括号的乘方项都替换为多个括号相乘。这样我们不带括号的表达式就只含加减乘了。Expression类的作用就是解析不带括号的最基本表达式。Factor类囊括了两种因子,幂函数和常数因子。由于不知道如何处理表达式因子,我建立了Cop和Kop类,其具体表现为提取括号内的字符串,再送到Expression类中解析,最后完成计算。Mul类是进行多项式乘法与加法的类,我并没有将减法纳入运算,遇到减法时我会建立多项式后将多项式内系数取反,对项也是同理。
1.2复杂性度量
1.2.1类复杂度
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| Cop | 2.67 | 6 | 8 |
| Expression | 3.67 | 12 | 44 |
| Factor | 1.29 | 3 | 9 |
| Kop | 2.67 | 6 | 8 |
| Lexer | 2.67 | 5 | 8 |
| Main | 5 | 9 | 10 |
| MainClass | 1 | 1 | 1 |
| Mul | 2.33 | 3 | 7 |
| Term | 1.45 | 4 | 16 |
可见对于Main与Expression类来说,圈复杂度较高,具体表现为进行了大量的if条件句判断,因为我没有在项与表达式中加入符号项,所以每次遇到正负号都需要用if条件句以进行是否让系数取反的判断。并且Expression中的方法复杂度之和较高。
1.2.2方法复杂度
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Cop.getFactors() | 0 | 1 | 1 | 1 |
| Cop.setCops() | 9 | 1 | 5 | 7 |
| Cop.setInput(String) | 0 | 1 | 1 | 1 |
| Expression.Expression(String) | 0 | 1 | 1 | 1 |
| Expression.didi() | 11 | 1 | 7 | 7 |
| Expression.getTerms() | 0 | 1 | 1 | 1 |
| Expression.hebin() | 6 | 1 | 4 | 4 |
| Expression.ptr() | 4 | 1 | 3 | 3 |
| Expression.qufan() | 1 | 1 | 2 | 2 |
| Expression.reptr() | 20 | 4 | 11 | 12 |
| Expression.setInput(String) | 0 | 1 | 1 | 1 |
| Expression.setTerms(Term) | 0 | 1 | 1 | 1 |
| Expression.wo(Term) | 12 | 8 | 8 | 8 |
| Expression.zhao() | 4 | 4 | 3 | 4 |
| Expression.zz() | 0 | 1 | 1 | 1 |
| Factor.Factor(String) | 5 | 1 | 3 | 3 |
| Factor.getCishu() | 0 | 1 | 1 | 1 |
| Factor.getInput() | 0 | 1 | 1 | 1 |
| Factor.getXishu() | 0 | 1 | 1 | 1 |
| Factor.setCishu(BigInteger) | 0 | 1 | 1 | 1 |
| Factor.setInput(String) | 0 | 1 | 1 | 1 |
| Factor.setXishu(BigInteger) | 0 | 1 | 1 | 1 |
| Kop.getKops() | 0 | 1 | 1 | 1 |
| Kop.setInput(String) | 0 | 1 | 1 | 1 |
| Kop.setTerms() | 16 | 1 | 10 | 15 |
| Lexer.Lexer(String) | 1 | 1 | 2 | 2 |
| Lexer.getInput() | 0 | 1 | 1 | 1 |
| Lexer.way1(String, String) | 7 | 2 | 2 | 5 |
| Main.main() | 27 | 6 | 7 | 10 |
| Main.setInput(String) | 0 | 1 | 1 | 1 |
| MainClass.main(String[]) | 0 | 1 | 1 | 1 |
| Mul.Mul(Expression, Expression) | 0 | 1 | 1 | 1 |
| Mul.jiafa() | 2 | 1 | 3 | 3 |
| Mul.jieguo() | 3 | 1 | 3 | 3 |
| Term.Term() | 0 | 1 | 1 | 1 |
| Term.Term(String) | 0 | 1 | 1 | 1 |
| Term.didi() | 7 | 1 | 5 | 5 |
| Term.getCishu() | 0 | 1 | 1 | 1 |
| Term.getInput() | 0 | 1 | 1 | 1 |
| Term.getXishu() | 0 | 1 | 1 | 1 |
| Term.setCishu(BigInteger) | 0 | 1 | 1 | 1 |
| Term.setInput(String) | 0 | 1 | 1 | 1 |
| Term.setXishu(BigInteger) | 0 | 1 | 1 | 1 |
| Term.wayCi() | 1 | 1 | 2 | 2 |
| Term.wayXi() | 1 | 1 | 2 | 2 |
与类中一样,复杂度较高的方法都利用了大量的条件语句,比如Expression的reptr类,这是最后简化输出用的,需要进行大量的判断来决定输出的内容。
2.第二次作业
2.1类图与设计思路
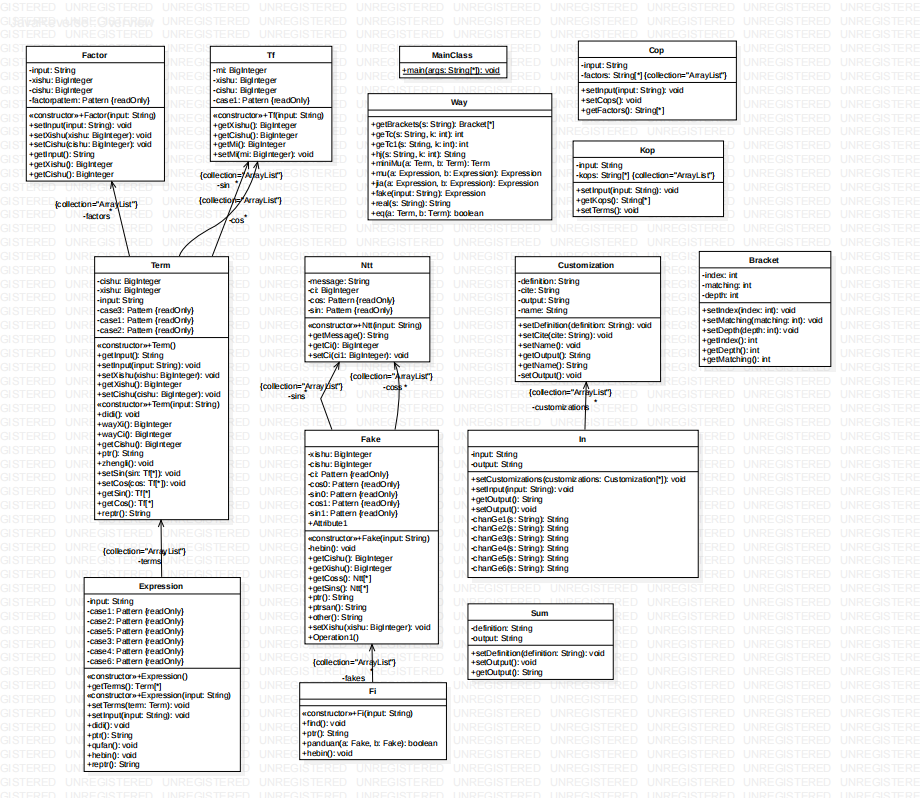
本次作业依旧采取了字符串处理,解析表达式,简化输出的思路。与第一次作业相比,多了三角函数类Tf,多了输出简化类Ntt,Fake,Fi,同时将输入处理类替换为In。建立了自定义函数Customization,与求和函数Sum,这两个类我认为属于输入处理类,与因子类不同,不能参与计算,具体作用是给定输入后可以将替换后的字符串输出出来。替换思路是将f,g,h三种函数分别进行替换,再将sin,cos分别换成p和q,再进行sum函数的替换,再将p()替换为p<>,最后将带括号的乘方表达式替换为多个表达式相乘。这里注意到,我们进行字符串替换的过程中,为了保持结果的正确性,需要对替换的内容,输出的结果都加上括号,所以不可避免的造成了嵌套括号,所以这就需要我们处理嵌套括号了。我对于嵌套括号的处理是,建立Bracket类,给出字符串中任何一个左括号的索引,找到该左括号对应的右括号,并且给出这对括号的内部括号最深有多少层。完成这步工作后,我们可以轻松地处理任何括号的嵌套问题。
对于嵌套括号乘方的替换,我们可以遍历整个字符串,找到左括号,得到右括号,判断右括号右边是否是^(已替换),再进行字符串替换,这样保证了乘方的替换不会出现差错。对于表达式的解析,由于不会使用hashmap,我在项中引入了两个ArrayList来存sin和cos,这样导致无论是计算,还是简化输出,都需要不停地遍历列表,这属于设计的失败点。对于解析有嵌套括号的表达式,根据第一次作业,已知可以解析含一层括号的表达式,通过寻找内部括号最深只有一层的一对括号,调用第一次作业进行解析,得出结果将括号替换掉,不断循环,直到字符串内只含有一层括号为止。这样就完成了嵌套括号的处理。
对于表达式的简化,第二次作业我遇到了sin(x)*(sin(x)+cos(x)) = sin(x)**2+sin(x)**2cos(x)的情况,由于没有想到好的处理方案,只能将输出重新处理一遍再进行化简,最后造成程序结构十分复杂。但由于第二次作业已经可以处理嵌套括号,并且函数替换不影响函数的互相调用,对第三次作业仍具有较好的扩展性。
2.2复杂性度量
2.1.1类复杂度
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| Bracket | 1 | 1 | 6 |
| Cop | 3 | 7 | 9 |
| Customization | 1.5 | 3 | 9 |
| Expression | 2.6 | 7 | 26 |
| Factor | 1.29 | 3 | 9 |
| Fake | 4.6 | 11 | 46 |
| Fi | 5.8 | 12 | 29 |
| In | 4.6 | 8 | 46 |
| Kop | 3 | 7 | 9 |
| MainClass | 2 | 2 | 2 |
| Ntt | 1.5 | 3 | 6 |
| Sum | 2.67 | 6 | 8 |
| Term | 2.5 | 12 | 45 |
| Tf | 1.2 | 2 | 6 |
| Way | 5.3 | 14 | 53 |
Way这个类包含了很多方法函数,比如求括号深度,多项式计算等等函数,有很强的面向过程的感觉,下次作业中应该避免写出这样的函数。Fake与Fi中进行了大量的if判断进行化简与简化输出造成圈复杂度较大。
2.2.2方法复杂度
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Bracket.getDepth() | 0 | 1 | 1 | 1 |
| Bracket.getIndex() | 0 | 1 | 1 | 1 |
| Bracket.getMatching() | 0 | 1 | 1 | 1 |
| Bracket.setDepth(int) | 0 | 1 | 1 | 1 |
| Bracket.setIndex(int) | 0 | 1 | 1 | 1 |
| Bracket.setMatching(int) | 0 | 1 | 1 | 1 |
| Cop.getFactors() | 0 | 1 | 1 | 1 |
| Cop.setCops() | 12 | 1 | 5 | 8 |
| Cop.setInput(String) | 0 | 1 | 1 | 1 |
| Customization.getName() | 0 | 1 | 1 | 1 |
| Customization.getOutput() | 0 | 1 | 1 | 1 |
| Customization.setCite(String) | 0 | 1 | 1 | 1 |
| Customization.setDefinition(String) | 0 | 1 | 1 | 1 |
| Customization.setName() | 3 | 1 | 2 | 3 |
| Customization.setOutput() | 1 | 1 | 2 | 2 |
| Expression.Expression() | 0 | 1 | 1 | 1 |
| Expression.Expression(String) | 0 | 1 | 1 | 1 |
| Expression.didi() | 12 | 1 | 9 | 9 |
| Expression.getTerms() | 0 | 1 | 1 | 1 |
| Expression.hebin() | 7 | 1 | 5 | 5 |
| Expression.ptr() | 6 | 3 | 3 | 4 |
| Expression.qufan() | 1 | 1 | 2 | 2 |
| Expression.reptr() | 6 | 3 | 3 | 4 |
| Expression.setInput(String) | 0 | 1 | 1 | 1 |
| Expression.setTerms(Term) | 0 | 1 | 1 | 1 |
| Factor.Factor(String) | 5 | 1 | 3 | 3 |
| Factor.getCishu() | 0 | 1 | 1 | 1 |
| Factor.getInput() | 0 | 1 | 1 | 1 |
| Factor.getXishu() | 0 | 1 | 1 | 1 |
| Factor.setCishu(BigInteger) | 0 | 1 | 1 | 1 |
| Factor.setInput(String) | 0 | 1 | 1 | 1 |
| Factor.setXishu(BigInteger) | 0 | 1 | 1 | 1 |
| Fake.Fake(String) | 17 | 4 | 10 | 11 |
| Fake.getCishu() | 0 | 1 | 1 | 1 |
| Fake.getCoss() | 0 | 1 | 1 | 1 |
| Fake.getSins() | 0 | 1 | 1 | 1 |
| Fake.getXishu() | 0 | 1 | 1 | 1 |
| Fake.hebin() | 12 | 1 | 7 | 7 |
| Fake.other() | 12 | 8 | 8 | 8 |
| Fake.ptr() | 17 | 3 | 12 | 12 |
| Fake.ptrsan() | 14 | 5 | 7 | 7 |
| Fake.setXishu(BigInteger) | 0 | 1 | 1 | 1 |
| Fi.Fi(String) | 5 | 1 | 4 | 4 |
| Fi.find() | 7 | 4 | 4 | 4 |
| Fi.hebin() | 6 | 1 | 4 | 4 |
| Fi.panduan(Fake, Fake) | 21 | 12 | 5 | 14 |
| Fi.ptr() | 7 | 4 | 4 | 5 |
| In.chanGe1(String) | 21 | 1 | 8 | 10 |
| In.chanGe2(String) | 21 | 1 | 8 | 10 |
| In.chanGe3(String) | 21 | 1 | 8 | 10 |
| In.chanGe4(String) | 12 | 1 | 6 | 8 |
| In.chanGe5(String) | 14 | 1 | 8 | 10 |
| In.chanGe6(String) | 12 | 6 | 4 | 6 |
| In.getOutput() | 0 | 1 | 1 | 1 |
| In.setCustomizations(ArrayList |
0 | 1 | 1 | 1 |
| In.setInput(String) | 0 | 1 | 1 | 1 |
| In.setOutput() | 0 | 1 | 1 | 1 |
| Kop.getKops() | 0 | 1 | 1 | 1 |
| Kop.setInput(String) | 0 | 1 | 1 | 1 |
| Kop.setTerms() | 21 | 1 | 12 | 19 |
| MainClass.main(String[]) | 1 | 1 | 2 | 2 |
| Ntt.Ntt(String) | 2 | 1 | 3 | 3 |
| Ntt.getCi() | 0 | 1 | 1 | 1 |
| Ntt.getMessage() | 0 | 1 | 1 | 1 |
| Ntt.setCi(BigInteger) | 0 | 1 | 1 | 1 |
| Sum.getOutput() | 0 | 1 | 1 | 1 |
| Sum.setDefinition(String) | 0 | 1 | 1 | 1 |
| Sum.setOutput() | 14 | 1 | 6 | 6 |
| Term.Term() | 0 | 1 | 1 | 1 |
| Term.Term(String) | 0 | 1 | 1 | 1 |
| Term.didi() | 27 | 1 | 13 | 13 |
| Term.getCishu() | 0 | 1 | 1 | 1 |
| Term.getCos() | 0 | 1 | 1 | 1 |
| Term.getInput() | 0 | 1 | 1 | 1 |
| Term.getSin() | 0 | 1 | 1 | 1 |
| Term.getXishu() | 0 | 1 | 1 | 1 |
| Term.ptr() | 8 | 1 | 5 | 5 |
| Term.reptr() | 8 | 1 | 5 | 5 |
| Term.setCishu(BigInteger) | 0 | 1 | 1 | 1 |
| Term.setCos(ArrayList |
0 | 1 | 1 | 1 |
| Term.setInput(String) | 0 | 1 | 1 | 1 |
| Term.setSin(ArrayList |
0 | 1 | 1 | 1 |
| Term.setXishu(BigInteger) | 0 | 1 | 1 | 1 |
| Term.wayCi() | 1 | 1 | 2 | 2 |
| Term.wayXi() | 1 | 1 | 2 | 2 |
| Term.zhengli() | 14 | 1 | 7 | 9 |
| Tf.Tf(String) | 2 | 1 | 2 | 2 |
| Tf.getCishu() | 0 | 1 | 1 | 1 |
| Tf.getMi() | 0 | 1 | 1 | 1 |
| Tf.getXishu() | 0 | 1 | 1 | 1 |
| Tf.setMi(BigInteger) | 0 | 1 | 1 | 1 |
| Way.eq(Term, Term) | 3 | 1 | 3 | 4 |
| Way.fake(String) | 27 | 6 | 7 | 10 |
| Way.geTc(String, int) | 7 | 4 | 4 | 5 |
| Way.geTc1(String, int) | 7 | 4 | 3 | 5 |
| Way.getBrackets(String) | 31 | 8 | 12 | 14 |
| Way.hj(String, int) | 8 | 2 | 4 | 4 |
| Way.jia(Expression, Expression) | 2 | 1 | 3 | 3 |
| Way.miniMu(Term, Term) | 4 | 1 | 5 | 5 |
| Way.mu(Expression, Expression) | 3 | 1 | 3 | 3 |
| Way.real(String) | 13 | 5 | 5 | 6 |
分析方法可知,复杂度高的方法都来源于字符串处理的替换部分与输出结果的转化部分,而且这类方法最主要的特性我认为都是面向过程的,并且复杂度高的方法容易出现bug,因此少设计这种方法是非常必要的。并且应该将每个类用到的方法放到它们自己中,不应该单独建立一个Way类。
3.第三次作业
3.1类图与设计思路
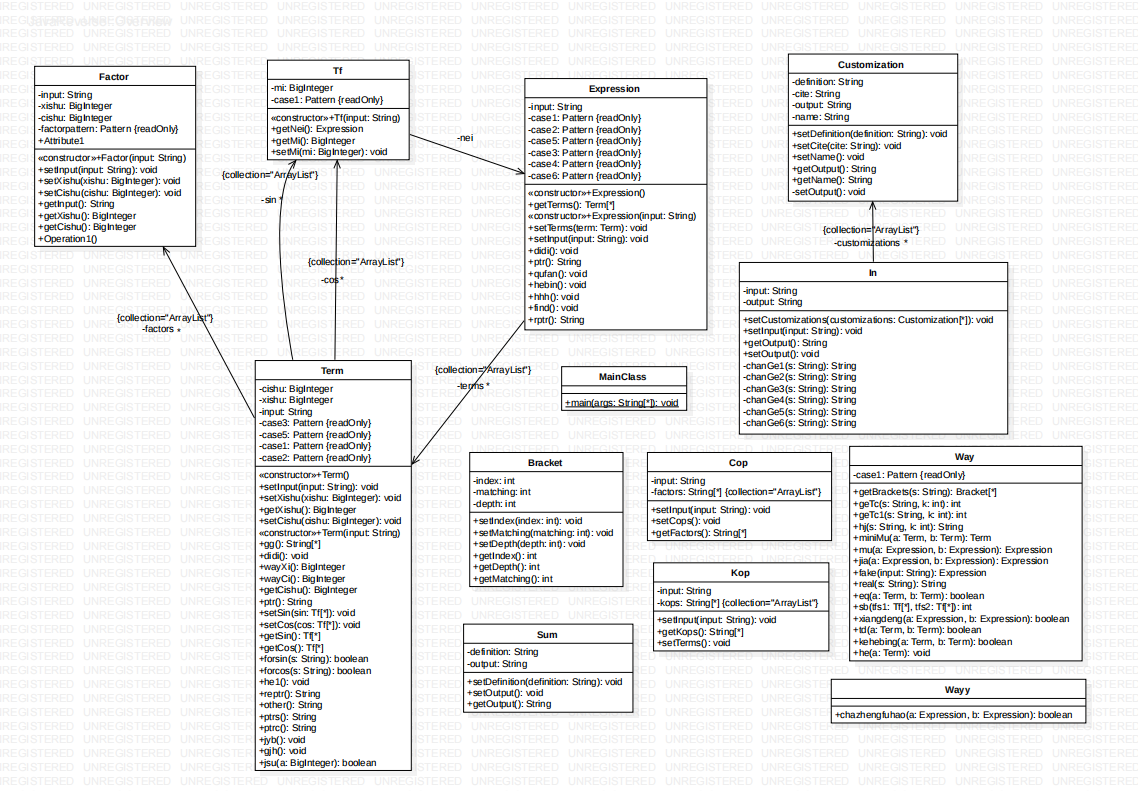
由于第二次作业已经提前支持了函数互相调用与任意层括号嵌套,所以第三次作业相比于第二次作业改动的位置是三角函数的内容,三角函数的内容从原先的描述x的次数与系数变成了内容是一个表达式,在对这部分进行处理的时候我也逐渐感受到了递归下降的意思。并且解决了第二次作业的bug,将输出与化简在类的内部完成,不用重新建立新类。
3.2复杂性度量
3.2.1类复杂度
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| Bracket | 1 | 1 | 6 |
| Cop | 4 | 10 | 12 |
| Customization | 2.33 | 7 | 14 |
| Expression | 3.08 | 9 | 37 |
| Factor | 1.29 | 3 | 9 |
| In | 4.7 | 8 | 47 |
| Kop | 4 | 10 | 12 |
| MainClass | 5 | 5 | 5 |
| Sum | 3 | 7 | 9 |
| Term | 4.12 | 12 | 107 |
| Tf | 1.75 | 4 | 7 |
| Way | 7.07 | 14 | 106 |
| Wayy | 13 | 13 | 13 |
可以看出,复杂度较高的部分依然包含输入字符串的处理以及输出字符串的化简这两部分的功能。并且Way以及超过了500行,要再写一个Wayy来拓展功能,导致这两个类复杂度很高。
3.2.2方法复杂度
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Bracket.getDepth() | 0 | 1 | 1 | 1 |
| Bracket.getIndex() | 0 | 1 | 1 | 1 |
| Bracket.getMatching() | 0 | 1 | 1 | 1 |
| Bracket.setDepth(int) | 0 | 1 | 1 | 1 |
| Bracket.setIndex(int) | 0 | 1 | 1 | 1 |
| Bracket.setMatching(int) | 0 | 1 | 1 | 1 |
| Cop.getFactors() | 0 | 1 | 1 | 1 |
| Cop.setCops() | 19 | 1 | 6 | 12 |
| Cop.setInput(String) | 0 | 1 | 1 | 1 |
| Customization.getName() | 0 | 1 | 1 | 1 |
| Customization.getOutput() | 0 | 1 | 1 | 1 |
| Customization.setCite(String) | 0 | 1 | 1 | 1 |
| Customization.setDefinition(String) | 0 | 1 | 1 | 1 |
| Customization.setName() | 3 | 1 | 2 | 3 |
| Customization.setOutput() | 12 | 1 | 5 | 8 |
| Expression.Expression() | 0 | 1 | 1 | 1 |
| Expression.Expression(String) | 0 | 1 | 1 | 1 |
| Expression.didi() | 27 | 1 | 14 | 20 |
| Expression.find() | 7 | 4 | 4 | 4 |
| Expression.getTerms() | 0 | 1 | 1 | 1 |
| Expression.hebin() | 7 | 1 | 5 | 5 |
| Expression.hhh() | 6 | 1 | 4 | 4 |
| Expression.ptr() | 7 | 3 | 4 | 5 |
| Expression.qufan() | 1 | 1 | 2 | 2 |
| Expression.rptr() | 5 | 3 | 3 | 4 |
| Expression.setInput(String) | 0 | 1 | 1 | 1 |
| Expression.setTerms(Term) | 0 | 1 | 1 | 1 |
| Factor.Factor(String) | 5 | 1 | 3 | 3 |
| Factor.getCishu() | 0 | 1 | 1 | 1 |
| Factor.getInput() | 0 | 1 | 1 | 1 |
| Factor.getXishu() | 0 | 1 | 1 | 1 |
| Factor.setCishu(BigInteger) | 0 | 1 | 1 | 1 |
| Factor.setInput(String) | 0 | 1 | 1 | 1 |
| Factor.setXishu(BigInteger) | 0 | 1 | 1 | 1 |
| In.chanGe1(String) | 22 | 1 | 9 | 11 |
| In.chanGe2(String) | 22 | 1 | 9 | 11 |
| In.chanGe3(String) | 22 | 1 | 9 | 11 |
| In.chanGe4(String) | 13 | 1 | 7 | 9 |
| In.chanGe5(String) | 17 | 1 | 11 | 12 |
| In.chanGe6(String) | 12 | 6 | 4 | 6 |
| In.getOutput() | 0 | 1 | 1 | 1 |
| In.setCustomizations(ArrayList |
0 | 1 | 1 | 1 |
| In.setInput(String) | 0 | 1 | 1 | 1 |
| In.setOutput() | 0 | 1 | 1 | 1 |
| Kop.getKops() | 0 | 1 | 1 | 1 |
| Kop.setInput(String) | 0 | 1 | 1 | 1 |
| Kop.setTerms() | 28 | 1 | 12 | 23 |
| MainClass.main(String[]) | 6 | 1 | 5 | 5 |
| Sum.getOutput() | 0 | 1 | 1 | 1 |
| Sum.setDefinition(String) | 0 | 1 | 1 | 1 |
| Sum.setOutput() | 15 | 1 | 7 | 7 |
| Term.Term() | 0 | 1 | 1 | 1 |
| Term.Term(String) | 0 | 1 | 1 | 1 |
| Term.didi() | 27 | 1 | 13 | 13 |
| Term.forcos(String) | 5 | 4 | 2 | 4 |
| Term.forsin(String) | 5 | 4 | 2 | 4 |
| Term.getCishu() | 0 | 1 | 1 | 1 |
| Term.getCos() | 0 | 1 | 1 | 1 |
| Term.getSin() | 0 | 1 | 1 | 1 |
| Term.getXishu() | 0 | 1 | 1 | 1 |
| Term.gg() | 11 | 1 | 4 | 7 |
| Term.gjh() | 16 | 1 | 8 | 8 |
| Term.he1() | 12 | 1 | 7 | 7 |
| Term.jsu(BigInteger) | 5 | 6 | 1 | 6 |
| Term.jyb() | 8 | 4 | 6 | 7 |
| Term.other() | 12 | 8 | 8 | 8 |
| Term.ptr() | 6 | 1 | 5 | 5 |
| Term.ptrc() | 17 | 3 | 16 | 17 |
| Term.ptrs() | 17 | 3 | 13 | 16 |
| Term.reptr() | 23 | 1 | 13 | 13 |
| Term.setCishu(BigInteger) | 0 | 1 | 1 | 1 |
| Term.setCos(ArrayList |
0 | 1 | 1 | 1 |
| Term.setInput(String) | 0 | 1 | 1 | 1 |
| Term.setSin(ArrayList |
0 | 1 | 1 | 1 |
| Term.setXishu(BigInteger) | 0 | 1 | 1 | 1 |
| Term.wayCi() | 1 | 1 | 2 | 2 |
| Term.wayXi() | 1 | 1 | 2 | 2 |
| Tf.Tf(String) | 8 | 1 | 4 | 4 |
| Tf.getMi() | 0 | 1 | 1 | 1 |
| Tf.getNei() | 0 | 1 | 1 | 1 |
| Tf.setMi(BigInteger) | 0 | 1 | 1 | 1 |
| Way.eq(Term, Term) | 3 | 1 | 3 | 4 |
| Way.fake(String) | 27 | 6 | 7 | 10 |
| Way.geTc(String, int) | 7 | 4 | 4 | 5 |
| Way.geTc1(String, int) | 7 | 4 | 3 | 5 |
| Way.getBrackets(String) | 31 | 8 | 12 | 14 |
| Way.he(Term) | 12 | 1 | 7 | 7 |
| Way.hj(String, int) | 8 | 2 | 4 | 4 |
| Way.jia(Expression, Expression) | 2 | 1 | 3 | 3 |
| Way.kehebing(Term, Term) | 27 | 14 | 5 | 14 |
| Way.miniMu(Term, Term) | 4 | 1 | 5 | 5 |
| Way.mu(Expression, Expression) | 3 | 1 | 3 | 3 |
| Way.real(String) | 13 | 5 | 5 | 6 |
| Way.sb(ArrayList |
12 | 6 | 3 | 6 |
| Way.td(Term, Term) | 26 | 13 | 5 | 13 |
| Way.xiangdeng(Expression, Expression) | 41 | 13 | 5 | 13 |
| Wayy.chazhengfuhao(Expression, Expression) | 40 | 13 | 5 | 13 |
除了与第二次作业相同的函数复杂度偏高之外,对三角函数判断相等以及化简部分的复杂度与耦合度都大幅度增加,因为三角函数的内部不再是简单的数或者幂函数,而是一个多项式了,对这些多项式判断相等显然更加复杂。
4.总结
4.1优点
逻辑简单,清晰易懂,对表达式的解析部分无需大改。
4.2缺点
面向对象的程度不够大,没有达到高内聚低耦合的要求,并且使用替换方法会出现意想不到的bug,类的抽象化程度不够高,要扩展只能从输入处理的部分下手。
二、程序的bug分析
1.第一次作业
第一次作业比较简单,没有被发现bug
2.第二次作业
在强测中被发现的bug是在计算的过程中如果出现0的话,替换的字符串是空串,这也是替换不好的一点,会有各种奇怪的bug出现。
在互测中被发现的bug是sin(0)**0我会输出0,我还思考了这个问题,没看题,擅自将其定义为1,并且sin(-1)**2我会直接将-1提出来,没有考虑幂次,属于考虑不周。
3.第三次作业
在强测与互测中都被发现了与化简输出有关的bug,具体描述为对于sin((sin(x)+cos(x)))我会少输出最外面的一层括号,这是因为判断方法出现了失误而导致的。并且在化简的过程中出现sin(0)也会出现bug。
4.总结
在经过程序分析后,我发现bug出现位置的方法都是圈复杂度较高,行数较多的方法,比如输出化简,嵌套括号替代等等位置,这也是因为我们无法很好地去预测复杂度高、行数多的代码的运行结果,更不好掌控这类方法,所以下次应该减少这类代码的出现,多减少耦合,多拆分方法。
三、测试与Hack策略
1.测试策略
我采用的测试策略是每写一个模块就进行一次测试,观察模块给出的输出是否与我预期的相同。如果每个模块的输出都跟预期的相同,那么最后输出的结果也大概率正确。在对一个模块进行测试时,要清晰的认知这个模块应该给出什么输出,比如测试函数替换模块时,我们可以先给出独立的函数进行测试,观察x,y,z顺序、个数不同时结果是否相同,在给出多个函数、函数与表达式进行加减运算等等多个情况观察替换结果是否相同。优点是测试逻辑清晰,也方便找出bug。缺点是如果有情况没有想到,模块组装起来后再去寻找bug较为困难。
2.Hack策略
首先我会输入几组在自己测试时觉得有坑的数据,再去观察别人的程序,首先看输出化简部分,我认为第一单元这里比较容易出错,另外正则表达式的使用也是这一单元容易出错的地方。
四、架构设计体验
1.第一次作业
刚接手到第一次作业,并没有什么思路,大概想了一想就直接开写了。并且由于没看懂练习中的代码,放弃了递归下降,一上来直接写了因子类,这也是我犯的第一个错误,将幂函数与常数因子放在一起进行统称Factor类,所以在后面处理表达式因子类以及三角函数因子、自定义函数因子等等其他因子时,都无法将它们抽象出来进行计算。这也算是惨痛的教训,下次作业一定要先构思好再开始写。因为没将表达式因子看成因子,所以只能将表达式的乘方化为相乘再进行计算,并引入两个新类来计算带一层括号的字符串,在写这两个类时,我感到他们与term和expression高度相似,顿时恍然大悟,但当时ddl将近,无奈无法引入接口Factor,只能硬着头皮写下去。并且各个类中含有大量的正则表达式匹配,在容易出错的同时还不利于扩展。
2.第二次作业
在第二次作业中,由于个人的懒惰,我没有选择进行重构,而是选择了扩展第一次作业的字符串替换方法,增加了自定义函数、求和函数的替换方法,并引入了新的三角函数类。在进行替换模块的测试时,总会出现一些奇奇怪怪的bug,这是替换方法的不好之处,并且替换还会带来很多括号,导致我的第二次作业就要适应任意层数的嵌套括号。
3.第三次作业
第三次作业中,函数互相调用与括号嵌套不是难点。我遇到的困难是当三角函数里面是表达式时,该如何判断当前是表达式、还是项或者因子的层级。因为前两次作业我都是用正则表达式进行判断的,但当三角函数中可以有表达式时,情况就会变得很复杂。所以基本到了第三次作业,我内部的所有条件语句判断全部由正则表达式改为了遍历字符串,这会使整个程序多了许多循环,是十分不好的。但在对三角函数内部的表达式进行分析的时候,我也逐渐懂得了递归下降的主要思想。
4.总结
经历了三次作业,我感受到好的架构是十分重要的,不要想到一种可能的方案就开始写,要综合思考,顾全大局。并且要少构建复杂度大的方法,我几乎所有的bug都是因此而出的,因为一旦考虑不周,就会有bug出现的风险。并且要勇于重构,我认为第二次作业重构的量应该与我在第二次作业中实际的工作量差不多。并且我认为解决问题要靠近问题的本质,字符串替换显然不是这三次作业问题的本质,所以适应字符串替换势必会导致吃力不讨好的结果。
五、心得体会
1.好的架构相当重要,要尝试去理解优秀的架构,千万不能闭门造车。
2.涉及条件判断的地方要仔细思考,尽量保证考虑的周全,弄清各个情况就是有没有交集,合在一起是不是整个集合。
3.先架构完全清楚之后,再写代码。
4.互测是很好的学习机会,不能光想着找bug,那些第一眼就觉得优秀的代码可以学习一下。
5.要提前拿出时间来写oo,后两次作业都是因为时间不足而导致丢分。
总的来说,每次完成作业时我都感到非常满足,这三周也算是对自己的一个磨砺,让我对面向对象有了初步的认识,代码能力有了一定的提升,并且学会了git、staruml等等工具,每一周都能感受到自己在进步。研讨课的热烈讨论也使我受益匪浅。第一单元结束了,感谢帮助过我的同学们,也感谢辛勤工作的助教们。同时第二单元开始了,我们也要继续进步。


