机器学习公开课笔记(7)：支持向量机
支持向量机(Support Vector Machine, SVM)
考虑logistic回归，对于$y=1$的数据，我们希望其$h_\theta(x) \approx 1$，相应的$\theta^Tx \gg 0$; 对于$y=0$的数据，我们希望$h_\theta(x) \approx 0$，相应的$\theta^Tx \ll 0$。每个数据点的代价为: $$-\left[y\log(h_\theta(x))+(1-y)\log(1-h\theta(x))\right]$$当$y=1$时其代价$cost_1(z)=-\log(\frac{1}{1+e^{-z}})$；当$y=0$时其代价$cost_0(z)=-\log(1-\frac{1}{1+e^{-z}})$，分别如图1左右所示。
图1 当$y=1$和$y=0$单个数据点的代价随$z$的变化
logistic回归的假设为$$\min\limits_\theta \frac{1}{m}\left[\sum\limits_{i=1}^{m}y^{(i)}(-\log(h_\theta(x^{(i)}))) + (1-y^{(i)})(-\log(1-h_\theta(x^{(i)})))\right] + \frac{\lambda}{2m}\sum\limits_{j=1}^{n}\theta_{j}^2$$通过去掉$\frac{1}{m}$并且将$A+\lambda B$的形式变为$CA+B$的形式，可以得到SVM的假设为$$\min\limits_\theta C\left[\sum\limits_{i=1}^{m}y^{(i)}cost_1(\theta^Tx^{(i)}) + (1-y^{(i)})cost_0(\theta^Tx^{(i)})\right] + \frac{1}{2}\sum\limits_{j=1}^{n}\theta_{j}^2$$
最大间隔(Large Margin Intuition)
对于$y=1$的数据，我们希望$\theta^Tx \ge 1$而不仅仅是$\ge 0$; 对于$y=0$的数据，我们希望$h_\theta(x) \leq -1$而不仅仅是$< 0$。当C很大时，由于$CA+B$要取最小值，因此$A\approx 0$，从而SVM最大化间隔问题变为\begin{align*}&\min\limits_\theta\frac{1}{2}\sum\limits_{j=1}^{n}\theta_j^{2}\\ &s.t.\quad\begin{cases}\theta^{T}x^{(i)}\geq 1 \quad y^{(i)}=1\\\theta^{T}x^{(i)}\leq -1 \quad y^{(i)}=0\end{cases}\end{align*}
图2 支持向量机最优超平面和最大Margin（两条虚线之间的距离），支撑向量指的是位于两条虚线上的点（在高维空间中，每个点可以看作是从原点出发的向量，所以这些点也称为向量）
参数C表示对错误的容忍程度，C值越大表示越不能容忍错误分类，容易出现过拟合现象（如图3所示）.
图3 参数C对分类的影响，C越大越不能容忍错误分类；反之能够接受少量错误分类.
Kernel
对于低维空间中线性不可分的情况，可以通过增加高阶多项式项将其映射到高维空间，使得在高维空间中通过一个超平面可分（如图4所示）。Kernel解决如何选择合适的高维特征问题，对于任意低维数据点x，定义它与低维空间中预先选定的标记点$l^{(i)}$（landmarks）之间的相似性为$$f_i=similarity(x, l^{(i)})=exp\left(-\frac{||x-l^{(i)}||^2}{2\sigma^2}\right)$$这样当有k个landmarks时，我们将得到k个新的特征$f_i$,这样就将低维空间的点x投射为高维（k维）空间中一个点。如果x距离$l^{(i)}$非常近，即$x\approx l^{(i)}$， 则相似性$f_i\approx 1$; 否则如果x距离$l^{(i)}$非常远，则相似性$f_i\approx 0$。接下来一个问题是如何选择landmarks，一种做法是选择所有的m个样本点作为landmarks，这样对于具有n个特征的数据点$x^{(i)}$，通过计算$f_i$，将得到一个具有m维空间的数据点$f^{(i)}$。
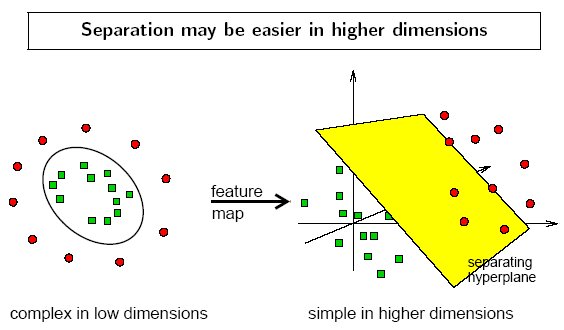
图4 通过kernel函数将低维线性不可分数据投射到高维空间从而使得线性可分.
SVM with kernels
假设(Hypothesis)：给定数据点$x$，计算新的特征$f$。当$\theta^Tf \geq 0$时，预测$y=1$；反之，预测$y=0$。
训练(Training):$$\min\limits_\theta C\left[\sum\limits_{i=1}^{m}y^{(i)}cost_1(\theta^Tf^{(i)}) + (1-y^{(i)})cost_0(\theta^Tf^{(i)})\right] + \frac{1}{2}\sum\limits_{j=1}^{n}\theta_{j}^2$$
参数C($\approx\frac{1}{\lambda}$)的影响:
- large C: low bias, high variance
- small C: high bias, low variance
参数$\sigma^2$的影响：
- large $\sigma^2$：high bias, low variance ($f_i$ vary more smoothly)
- small $\sigma^2$：low bias, high variance ($f_i$ vary less smoothly)
支持向量机实践
实际应用中不会要求自己实现SVM，更多是调用线程的库例如liblinear，libsvm等来求解。需要指定参数C和kernel函数。
Linear kernel： 不指定kernel，即“No kernel”，也称为“linear kernel”（用于特征n较大，同时example数m较小时）.
Gaussian kernel: $f_i=exp\left(-\frac{||x-l^{(i)}||^2}{2\sigma^2}\right)$，其中$l^{(i)}=x^{(i)}$，需要指定参数$\sigma^2$(用于n较小，m较大时)。注意在使用Gaussian kernel之前需要对数据进行feature scaling.
其他常见的kernel包括
- Polynomal kernel：$k(x, l) = (\alpha x^Tl+c)^{d}$，其中可调节参数包括坡度$\alpha$，常量$c$和多项式度$d$
- string kernel: 对字符串直接进行变换，不需要将字符串数值化，具体公式见wikipedia:string kernel
- chi-square kernel：$k(x, y)=1-\sum\limits_{k=1}^{n}\frac{(x_k-y_k)^2}{\frac{1}{2}(x_k+y_k)}$
- histogram intersection kernel：$k(x, y) = \sum\limits_{k=1}^{n}\min(x_k, y_k)$
多元分类：采用one-vs-all的方法，对于k个分类，需要训练k个svm.
logistic回归和SVM
当n较大时（$n\geq m$, n=10000, m = 1000），使用logistic回归或者SVM(with linear kernel)
当n较小，m中等时（n=10-1000, m = 10-100000），使用SVM(with Gaussian kernel)
当n较小, m较大时（n=1-1000, m = 500000），增加新的特征，然后适用logistic回归或者SVM(with linear kernel)
神经网络在各类n, m情况下都工作的很好，缺陷是训练速度比较慢
参考文献
[1] Andrew Ng Coursera 公开课第七周
[2] Kernel Functions for Machine Learning Applications. http://crsouza.com/2010/03/kernel-functions-for-machine-learning-applications/#chisquare
[3] Wikipedia: string kernel. https://en.wikipedia.org/wiki/String_kernel
[4] Hofmann T, Schölkopf B, Smola A J. Kernel methods in machine learning[J]. The annals of statistics, 2008: 1171-1220.
