机器学习公开课笔记(3):Logistic回归
Logistic 回归
通常是二元分类器(也可以用于多元分类),例如以下的分类问题
- Email: spam / not spam
- Tumor: Malignant / benign
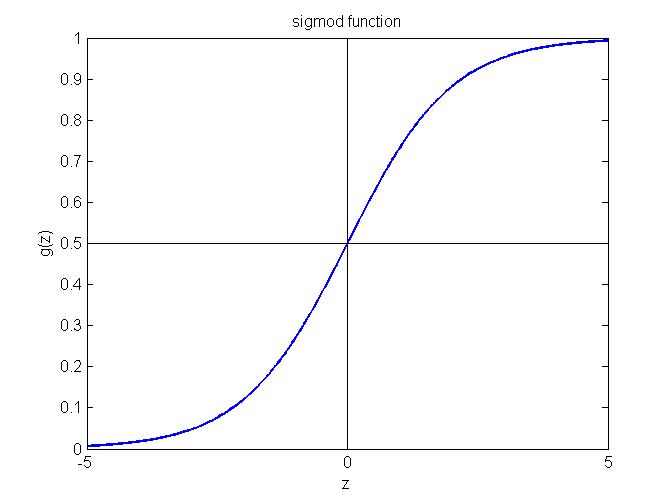
假设 (Hypothesis):$$h_\theta(x) = g(\theta^Tx)$$ $$g(z) = \frac{1}{1+e^{-z}}$$ 其中g(z)称为sigmoid函数,其函数图象如下图所示,可以看出预测值$y$的取值范围是(0, 1),这样对于 $h_\theta(x) \geq 0.5$, 模型输出 $y = 1$; 否则如果 $h_\theta(x) < 0.5$, 模型输出 $y = 0$。
1. 对于输出的解释
$h_\theta(x)$=该数据属于 $y=1$分类的概率, 即 $$h_\theta(x) = P\{y = 1|x; \theta\}$$ 此外由于y只能取0或者1两个值,换句话说,一个数据要么属于0分类要么属于1分类,假设已经知道了属于1分类的概率是p,那么当然其属于0分类的概率则为1-p,这样我们有以下结论 $$P(y=1|x;\theta) + P(y=0|x;\theta) = 1$$ $$P(y=0|x;\theta) = 1 - P(y = 1|x; \theta)$$
2. 决策边界(Decision Bound)
函数$g(z)$是单调函数,
- $h_\theta(x)\geq 0.5$预测输出$y=1$, 等价于$\theta^Tx \geq 0$预测输出$y=1$;
- $\theta(x) < 0.5$预测输出$y=0$, 等价于$\theta^Tx < 0$预测输出$y=0$;
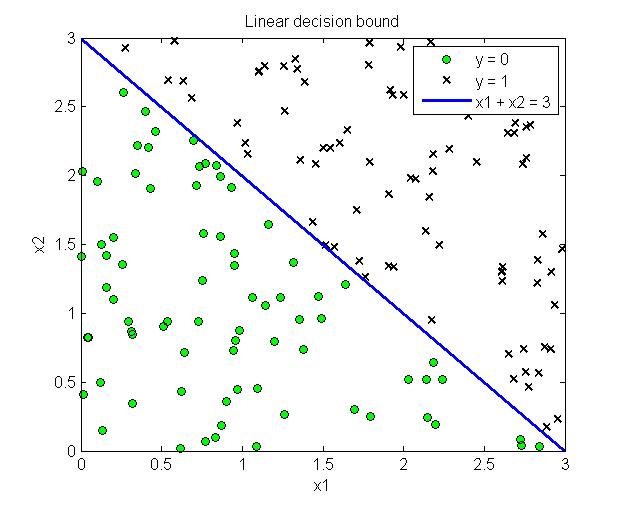
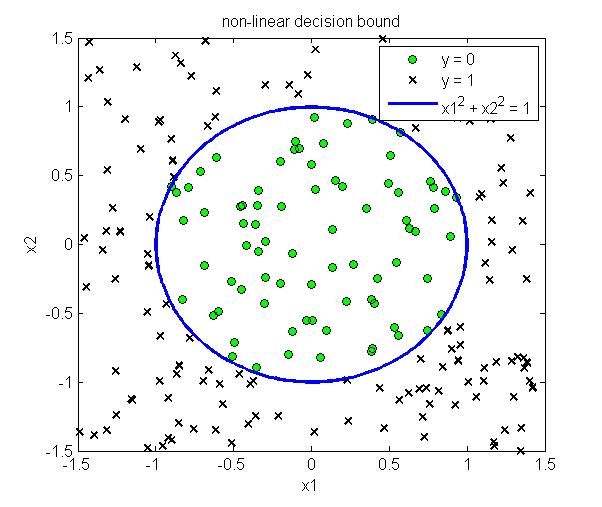
这样不需要具体的带入sigmoid函数,只需要求解$\theta^Tx \geq 0$即可以得到对应的分类边界。下图给出了线性分类边界和非线性分类边界的例子
3. 代价函数 (Cost Function)
在线性回归中我们定义的代价函数是,即采用最小二乘法来进行拟合
$$J(\theta)=\frac{1}{m}\sum\limits_{i=1}^{m}\text{cost}(h_\theta(x^{(i)}), y)$$ $$\text{cost}(h_\theta(x), y)=\frac{1}{2}(h_\theta(x)-y)^2$$
然而由于这里的假设是sigmoid函数,如果直接采用上面的代价函数,那么$J(\theta)$将会是非凸函数,无法用梯度下降法求解最小值,因此我们定义Logistic cost function为
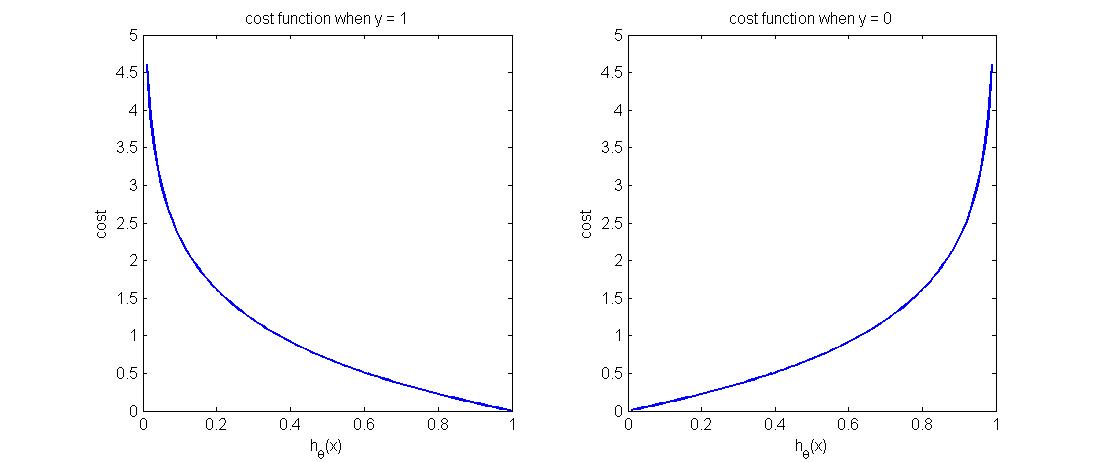
$$\text{cost}(h_\theta(x), y)=\begin{cases}-log(h_\theta(x)); y = 1\\ -log(1-h_\theta(x)); y = 0\end{cases}$$
函数图像如下图所示,可以看到,当$y=1$时,预测正确时($h_\theta(x)=1$)代价为零,反之预测错误时($h_\theta(x)=0$)的代价非常大,符合我们的预期。同理从右图可以看出,当y=0时,预测正确时($h_\theta(x)=0$)代价函数为0,反之预测错误时($h_\theta(x)=1$)代价则非常大。表明该代价函数定义的非常合理。
4. 简化的代价函数
前面的代价函数是分段函数,为了使得计算起来更加方便,可以将分段函数写成一个函数的形式,即
$$\text{cost}(h_\theta(x), y)=-y\log(h_\theta(x))-(1-y)\log(1-h_\theta(x))$$
$$J(\theta)=-\frac{1}{m}\sum\limits_{i=1}^{m}y^{(i)}\log(h_\theta(x^{(i)})) + (1-y^{(i)})\log(1-h_\theta(x^{(i)}))$$
梯度下降
有了代价函数,问题转化成一个求最小值的优化问题,可以用梯度下降法进行求解,参数$\theta$的更新公式为
$$\theta_j = \theta_j - \alpha \frac{\partial}{\partial \theta_j}J(\theta)$$
其中对$J(\theta)$的偏导数为 $$\frac{\partial}{\partial \theta_j}J(\theta) = \frac{1}{m}\sum\limits_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}$$ 注意在logistic回归中,我们的假设函数$h_\theta(x)$变了(加入了sigmoid函数),代价函数$J(\theta)$也变了(取负对数,而不是最小二乘法), 但是从上面的结果可以看出偏导数的结果完全和线性归回一模一样。那么参数$\theta$的更新公式也一样,如下
$$\theta_j = \theta_j - \alpha \frac{1}{m}\sum\limits_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}$$
为什么偏导数长这样子,为什么和线性回归中的公式一模一样?公开课中没有给出证明过程,主要是多次使用复合函数的链式求导法则,具体的证明过程可以看这里。我也提供一个更加简洁的证明过程如下,首先将$h_\theta(x^{(i)})$写成如下两个等式,即:$$h_\theta(x^{(i)})=g(z^{(i)})$$, $$g(z^{(i)})=\theta^Tx^{(i)}$$
其中$g(z)=\frac{1}{1+e^{-z}}$是sigmoid激活函数,对两个等式分别求导,有
$$\frac{d g(z)}{dz}=-1 \frac{1}{(1+e^{-z})^2}e^{-z}(-1)=\frac{e^{-z}}{(1+e^{-z})^2}=\frac{1}{1+e^{-z}}-\frac{1}{(1+e^-z)^2}=g(z)-g(z)^2=g(z)(1-g(z))$$
$$\frac{dz}{d\theta_j}=\frac{d(\theta^Tx)}{d\theta_j}=\frac{d(\theta_0+\theta_1x_1+\theta_2x_2+\ldots+\theta_nx_n)}{d\theta_j}=x_j$$
然后我们开始对代价函数$$J(\theta)=-\frac{1}{m}\sum\limits_{i=1}^{m}y^{(i)}\log(h_\theta(x^{(i)})) + (1-y^{(i)})\log(1-h_\theta(x^{(i)}))$$求偏导数
\begin{aligned}\frac{\partial J(\theta)}{\partial \theta_j}&=-\frac{1}{m}\sum\limits_{i=1}^{m}y^{(i)}\frac{1}{g(z^{(i)})}g'(z^{(i)})\frac{dz}{d\theta_j}+(1-y^{(i)})\frac{1}{1-g(z^{(i)})}(-1)g'(z^{(i)})\frac{dz}{d\theta_j}\\ &= -\frac{1}{m}\sum\limits_{i=1}^{m}y^{(i)}\frac{1}{g(z^{(i)})}g(z^{(i)})(1-g(z^{(i)}))x_j^{(i)}+(1-y^{(i)})\frac{1}{1-g(z^{(i)})}(-1)g(z^{(i)})(1-g(z^{(i)}))x_j^{(i)}\\ &= -\frac{1}{m}\sum\limits_{i=1}^{m}y^{(i)}(1-g(z^{(i)}))x_j^{(i)}+(y^{(i)}-1)g(z^{(i)})x_j^{(i)}\\ &=-\frac{1}{m}\sum\limits_{i=1}^{m}(y^{(i)}-g(z^{(i)}))x_j^{(i)}\\ &= \frac{1}{m}\sum\limits_{i=1}^{m}(g(z^{(i)})-y^{(i)})x_j^{(i)}\\ &=\frac{1}{m}\sum\limits_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}\end{aligned}
至此我们已经求出了logistic回归代价函数的偏导数,可以看出它和线性归回中采用最小二乘的代价函数的偏导数形式上是一样的。
高级优化算法
除了梯度下降算法,可以采用高级优化算法,比如下面的集中,这些算法优点是不需要手动选择$\alpha$,比梯度下降算法更快;缺点是算法更加复杂。
- conjugate gradient (共轭梯度法)
- BFGS (逆牛顿法的一种实现)
- L-BFGS(对BFGS的一种改进)
Logistic回归用于多元分类
Logistic回归可以用于多元分类,采用所谓的One-vs-All方法,具体来说,假设有K个分类{1,2,3,...,K},我们首先训练一个LR模型将数据分为属于1类的和不属于1类的,接着训练第二个LR模型,将数据分为属于2类的和不属于2类的,一次类推,直到训练完K个LR模型。
对于新来的example,我们将其带入K个训练好的模型中,分别其计算其预测值(前面已经解释过,预测值的大小表示属于某分类的概率),选择预测值最大的那个分类作为其预测分类即可。
Regularization
1. Overfitting (过拟合)
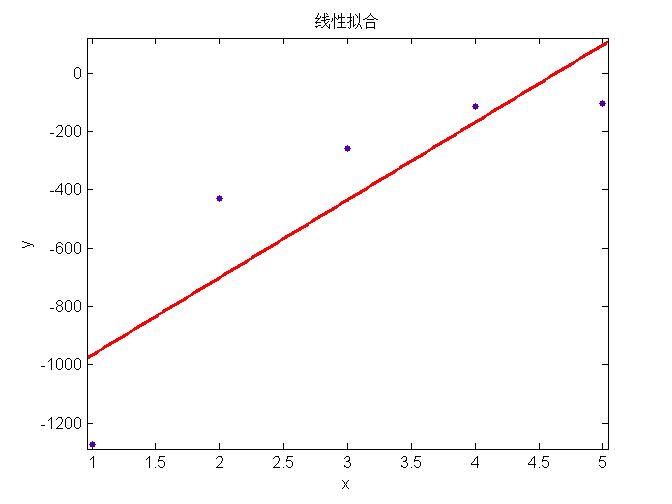

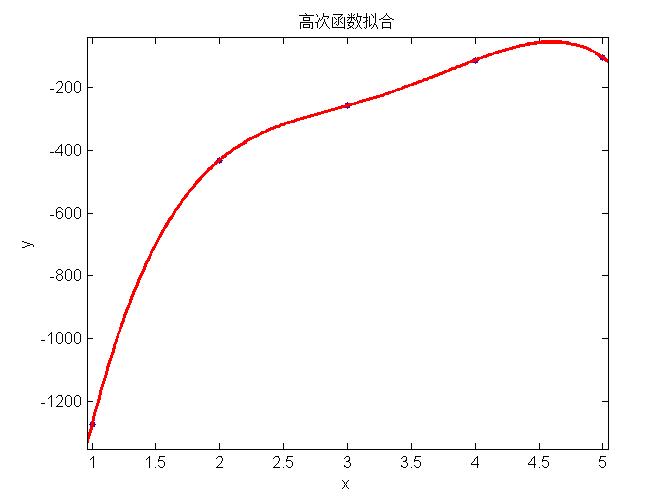
上面三幅图分别表示用简单模型、中等模型和复杂模型对数据进行回归,可以看出左边的模型太简单不能很好的表示数据特征(称为欠拟合, underfitting),中间的模型能够很好的表示模型的特征,右边使用最复杂的模型所有的数据都在回归曲线上,表面上看能够很好的吻合数据,然而当对新的example预测时,并不能很好的表现其趋势,称为过拟合(overfitting)。
Overfitting通常指当模型中特征太多时,模型对训练集数据能够很好的拟合(此时代价函数$J(\theta)$接近于0),然而当模型泛化(generalize)到新的数据时,模型的预测表现很差。
Overfitting的解决方案
- 减少特征数量:
- 人工选择重要特征,丢弃不必要的特征
- 利用算法进行选择(PCA算法等)
- Regularization
- 保持特征的数量不变,但是减少参数$\theta_j$的数量级或者值
- 这种方法对于有许多特征,并且每种特征对于结果的贡献都比较小时,非常有效
2. 线性回归的Regularization
在原来的代价函数中加入参数惩罚项如下式所示,注意惩罚项从$j=1$开始,第0个特征是全1向量,不需要惩罚。
代价函数:
$$J(\theta) = \frac{1}{2m}\left[ \sum\limits_{i=1}^{m} (h_\theta(x^{(i)})-y^{(i)})^2 + \lambda \sum\limits_{j=1}^{n}\theta_j^{2}\right]$$
梯度下降参数更新:
$$\theta_0 = \theta_0 - \alpha\frac{1}{m}\sum\limits_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_0^{(i)}; j = 0$$
$$\theta_j = \theta_j - \alpha \left[ \frac{1}{m}\sum\limits_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} + \frac{\lambda}{m}\theta_j \right]; j > 1$$
3. Logistic回归的Regularization
代价函数: $$J(\theta) = -\frac{1}{m} \sum\limits_{i=1}^{m}\left[y^{(i)}\log(h_\theta(x^{(i)})) +(1-y^{(i)})\log(1-h_\theta(x^{(i)}))\right] + \frac{\lambda}{2m}\sum\limits_{j=1}^{n}\theta_j^{2}$$
梯度下降参数更新:
$$\theta_0 = \theta_0 - \alpha\frac{1}{m}\sum\limits_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_0^{(i)}; j = 0$$
$$\theta_j = \theta_j - \alpha \left[ \frac{1}{m}\sum\limits_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} + \frac{\lambda}{m}\theta_j \right]; j > 1$$
参考文献
[1] Andrew Ng Coursera 公开课第三周
[2] Logistic cost function derivative: http://feature-space.com/en/post24.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号