Shamir秘密共享方案 (Python)
Shamir’s Secret Sharing scheme is an important cryptographic algorithm that allows private information— “secrets” — to be distributed securely amongst an untrusted network.
Shamir’s method for secret sharing relies on polynomial interpolation, which is an algebraic method of estimating unknown values in a gap between two known data points — without needing to know anything about what is on either side of those points.
SSS encodes a “secret” into a polynomial, then splits it into pieces and distributes it It’s possible to use polynomial interpolation to efficiently reconstruct that secret without requiring every single share. Instead only the threshold is needed, which provides enough points of data to correctly estimate the values between gaps in the encrypted shares.
REF: https://medium.com/keylesstech/a-beginners-guide-to-shamir-s-secret-sharing-e864efbf3648
Shamir秘密共享方案,叫做Shamir Secret Sharing, SSS。是由Shamir提出的一个分享密钥(本文秘密和“密钥”同义)的局部、并共同计算密钥的方法。
设计目的
假设公司A,B,C有一个密钥可以打开共同的仓库房门,为了防止保管人不在,或者被侵害,或者钥匙被偷,或者监守自盗。需要设计一个分享秘密的方案。
一个直观的方案就是将秘密分开为3份,给ABC各自钥匙的一部分,他们的子密钥合起来才能打开房门。
数学定义
引入一个临界点(Threshold,也叫门槛)的概念。N个分享秘密的人,只要凑够k个人(k<=N)就可以重建秘密。k就是这个临界点。
k<N,大大增加了使用的便利性和可扩展性。任意的k个人合起来都可以重建秘密,少于k个人无法重建秘密。
k=N,表明方案中所有的参与者需要贡献出自己的子秘密,才能合成所需的秘密。
举例
一个(k,N) 临界点方案,其共享秘密是 S.
对一个k-1次的多项式,取 N个不一样的点(i,f(i))。那么只要凑够 k个点就可以接出系数(a0,a1,……ak-1)。
![]()
只要把N个点分给N个人,设某个系数为共同秘密(如a0是秘密),那么就等于实现了SSS算法。
秘密分配及还原过程
首先介绍一个小费马定理:![]()
引申为:![]()
那么有:![]()
秘密碎片生成:
构造一个多项式
![]()
其中,S为我们的秘密,p为素数,且S < p
取w个不相等的x,带入F(x)中,得到w组(xi,yi),分配给w个人
公开p,销毁多项式,每个人负责保密自己的(xi,yi)
秘密恢复:
当x=0时,F(0)=S,即可恢复出S
将t组(xi,yi)带入下式即可
![]()
其中,负一次方为该项模p的逆
将t组(xi,yi)带入即可得到S
示例:
假设我们有w=4个人,设定至少t=3人才能恢复秘密。
秘密S=2,p=23
构造![]()
取x1=1,x2=2,x3=3,x4=4
带入得y1=7,y2=16, y3=6,y4=0
利用3组进行恢复(1,7) (3,6) (4,0)
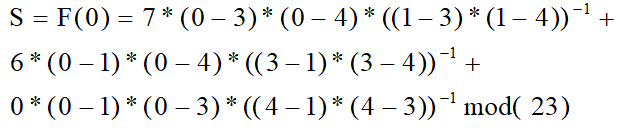
计算可得到S=2
一个简单的恢复脚本
1 # coding:utf-8 2 3 4 def oj(a, n): # 求逆的函数 5 a = a % n 6 s = [0, 1] 7 while a != 1: 8 if a == 0: 9 return 0 10 q = n/a 11 t = n % a 12 n = a 13 a = t 14 s += [s[-2] - q * s[-1]] 15 return s[-1] 16 17 p = 23 18 m = ((4, 0), 19 (3, 6), 20 (2, 16)) 21 r = ( 22 m[0][1] * (0 - m[1][0]) * (0 - m[2][0]) * oj((m[0][0] - m[1][0]) * (m[0][0] - m[2][0]), p) + 23 m[1][1] * (0 - m[0][0]) * (0 - m[2][0]) * oj((m[1][0] - m[0][0]) * (m[1][0] - m[2][0]), p) + 24 m[2][1] * (0 - m[0][0]) * (0 - m[1][0]) * oj((m[2][0] - m[0][0]) * (m[2][0] - m[1][0]), p) 25 ) % p 26 print r
另外一个脚本
1 import Crypto.Util.number as numb 2 import random 3 4 5 # 求逆的函数,之前的版本用python2写的,这次用的python3,只把整除符号改了一下 6 def oj(a, n): 7 a = a % n 8 s = [0, 1] 9 while a != 1: 10 if a == 0: 11 return 0 12 q = n // a 13 t = n % a 14 n = a 15 a = t 16 s += [s[-2] - q * s[-1]] 17 return s[-1] 18 19 20 # max_length 为p的长度,同时也是秘密的最大长度 21 # secret_is_text =0 默认输入时文本, 非0时认为是数字 22 # p 默认为0, 会根据max_length 自动生成,不为0时直接使用,需要保证p为素数, 函数内没有素性检验 23 def create(max_length=513, secret_is_text=0, p=0): 24 if not p: 25 p = numb.getPrime(max_length) 26 27 w = int(input("请输入秘密保存人数:")) 28 t = int(input("请输入秘密恢复所需人数:")) 29 while not (t > 0 and t <= w): 30 t = int(input("请重新输入:")) 31 s = input("请输入你的秘密:") 32 33 if secret_is_text: 34 s = numb.bytes_to_long(s.encode("utf-8")) 35 else: 36 try: 37 s = int(s) 38 except Exception as e: 39 s = numb.bytes_to_long(s.encode("utf-8")) 40 41 x_list = list() 42 a_list = list() 43 i = w 44 while i > 0: 45 x = random.randint(p // 2, p) # 该范围没有特定限制,如果想让xi,yi取小一点儿的话可把范围写小点儿,但是要大于w 46 if x not in x_list: 47 x_list.append(x) 48 i -= 1 49 50 for a in range(t): 51 a_list.append(random.randint(p // 2, p)) # 同上 52 53 result = list() 54 for x in x_list: 55 y = s 56 for a_n in range(t): 57 a = a_list[i] 58 y += a * pow(x, i + 1, p) 59 result.append((x, y)) 60 return t, p, result 61 62 63 # get_text=1 默认恢复为字符串,若想得到数字填0 64 def restore(p, information, get_text=1): 65 66 x_list = list() 67 y_list=list() 68 for x, y in information: 69 x_list.append(x) 70 y_list.append(y) 71 72 s = 0 73 for x_i in range(len(x_list)): 74 tmp_num = y_list[x_i] 75 x_i_j = 1 76 for x_j in range(len(x_list)): 77 if x_i != x_j: 78 tmp_num = tmp_num * (0 - x_list[x_j]) % p 79 x_i_j *= x_list[x_i] - x_list[x_j] 80 tmp_num = tmp_num * oj(x_i_j, p) % p 81 s += tmp_num 82 83 s = s % p 84 print(s) 85 if get_text: 86 try: 87 s = numb.long_to_bytes(s) 88 s = s.decode("utf-8") 89 except Exception as e: 90 print(e) 91 92 return s 93 94 95 t, p, result = create() #result为秘密碎片的列表 96 print(result) 97 print(restore(p, result[:t])) #这里我取了result的前t个,实际中可以取任意t个。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号