优化方法-momentum动量法和Adam
优化
在一个深度学习问题中,我们通常会预先定义一个损失函数。有了损失函数以后,我们就可以使用优化算法试图将其最小化。在优化中,这样的损失函数通常被称作优化问题的目标函数(objective function)。依据惯例,优化算法通常只考虑最小化目标函数。其实,任何最大化问题都可以很容易地转化为最小化问题,只需令目标函数的相反数为新的目标函数即可
由于优化算法的目标函数通常是一个基于训练数据集的损失函数,优化的目标在于降低训练误差。 而深度学习的目标在于降低泛化误差。为了降低泛化误差,除了使用优化算法降低训练误差以外,还需要注意应对过拟合。
momentum动量法
解决的问题:
同一位置上,目标函数在不同的参数方向斜率不同。例如2个参数,竖直方向( x2 轴方向)比在水平方向( x1 轴方向)的斜率的绝对值更大。因此,给定学习率,梯度下降迭代自变量时会使自变量在竖直方向比在水平方向移动幅度更大。那么,我们需要一个较小的学习率从而避免自变量在竖直方向上越过目标函数最优解。然而,这会造成自变量在水平方向上朝最优解移动变慢。而如果将学习率调得稍大一点,此时自变量在竖直方向不断越过最优解并逐渐发散
缺点
1、learning_rate一直不变
2、不同维度使用相同的learning_rate
实现方法-移动加权平均法
引入动量中间变量vt,在时间步 t>0 ,动量法对每次迭代的步骤做如下修改:
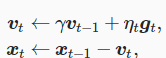
动量法使用了指数加权移动平均的思想。它将过去时间步的梯度做了加权平均,且权重按时间步指数衰减。
动量法使得相邻时间步的自变量更新在方向上更加一致。
AdaGrad
解决的问题
momentum动量法问题,lr一直不变和不同维度使用相同的lr
缺点
由于lr调整时分母一直按照各维度梯度平方累加,所以lr会一直降低;该种方式在开始时下降的比较快,但刚开始的解不好时,后期会因为lr过小导致比较难找到最优解。
实现方法-各维度自己计算和调整lr
lr的调整参数s计算公式为,其中乘法部分为小批量随机梯度各元素平方累加和:
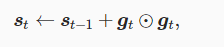
使用lr调整参数s计算梯度,其中色俺码为常数10(-6),维持稳定性,防止分母为0情况
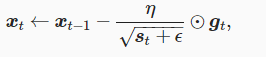
RMSProp(RMSProp算法和AdaGrad算法的不同在于,RMSProp算法使用了小批量随机梯度按元素平方的指数加权移动平均来调整学习率。)
解决的问题
AdaGrad 调整学习率时分母上的变量 st 一直在累加按元素平方的小批量随机梯度,所以目标函数自变量每个元素的学习率在迭代过程中一直在降低。因此,当学习率在迭代早期降得较快且当前解依然不佳时,AdaGrad算法在迭代后期由于学习率过小,可能较难找到一个有用的解
实现方法-对AdaGrad的lr调整变量s使用加权指数移动平均,这样每个元素的学习率在迭代过程中就不再一直降低
对AdaGrad的lr调整变量s使用加权指数移动平均
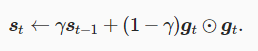
使用lr调整参数s计算梯度,其中色俺码为常数10(-6),维持稳定性,防止分母为0情况
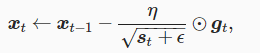
RMSProp,AdaGrad和Momentum SGD区别是后者lr不变和每个维度的lr相同,前者使每个维度lr不同,且lr随时间变化; AdaGrad的lr的调整参数是使用累加个维度的梯度平方,所以lr会持续下降,且刚开始下降较快,这样就导致如果刚开始没学习好效果,后续lr过小导致比较难训练最优解;而RMSProp的lr的调整参数是使用各维度梯度平方的 指数加权移动平均,解决了lr一直下降的问题
Adam-RMSProp算法与动量法的结合
实现方法
和动量发一样,计算t时间动量
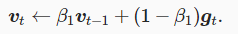
和RMSProp一样,计算t使用lr的调整参数
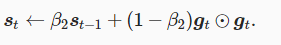
使用动量和lr调整参数计算梯度
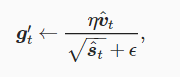
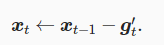


 浙公网安备 33010602011771号
浙公网安备 33010602011771号