线性回归调参

问题是，使用numpy实现线性回归，代码是这样的

################### 线性回归
## 模型 y = w*x + b
## Loss = (y-y_predient)^2 = (y - w * x - b)^2
## w' = 2 * (y - w * x - b) * (-x)
## b' = 2 * (y - w * x - b) * (-1)
######### 1 numpy实现
import numpy as np
from matplotlib import pyplot as plt

x = np.array([2013, 2014, 2015, 2016, 2017], dtype=np.float32)
y = np.array([12000, 14000, 15000, 16500, 17500], dtype=np.float32)

loss_list = []
def loss(y, y_predict):
    loss_list.append(((y - y_predict) ** 2).sum())
#     print(loss_list)

def draw_loss():
#     print(loss_list)
    x = np.arange(len(loss_list))
    y = loss_list
    plt.plot(x, y)
    plt.show()
    
def linear_regression(x, y):
    w, b = 6, 0
    epoch = 10000
    learning_rate = 0.000000245
    for i in range(epoch):
        y_predict = w * x + b
#         print(y_predict)
        loss(y, y_predict)
        w_gradient, b_gradient = 2 * (y - y_predict).dot(-x), 2 * (y - y_predict).sum() *  (-1)
#         print("w_gradient", w_gradient)
        w, b = w - learning_rate * w_gradient /len(x), b - learning_rate * b_gradient/len(x)
#         print(w, b)
    return w, b


w, b = linear_regression(x, y)
print(w, b)
print(loss_list[-1])
draw_loss()
print(w * 2017 + b)

1、loss函数越来越大

 原因是，learning_rate 大了，减小learning_rate

2、loss在一直在减小，但是最终效果不好

  原因是，learning_rate 小了，需要增大learning_rate

 

 

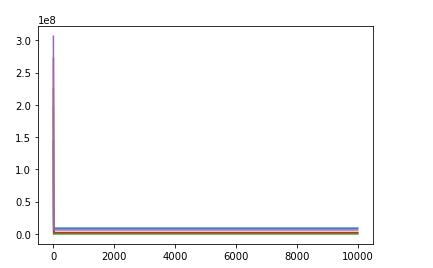
 但是，怎么调参都调不好，原因是x值范围是如果直接拟合这条直线，这条直线是非常难拟合的如下图

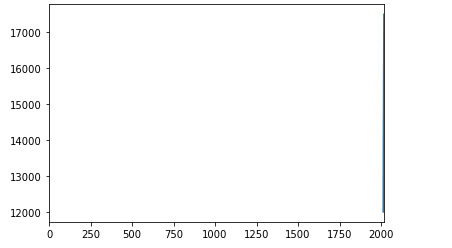
from matplotlib import pyplot as plt

x = [2013, 2014, 2015, 2016, 2017]
y = [12000, 14000, 15000, 16500, 17500]

plt.xlim(xmin=0, xmax=max(x))
plt.plot(x, y)
plt.show()

当我们对数据做标准化之后，需要拟合的数据就变成如下

 

 

 

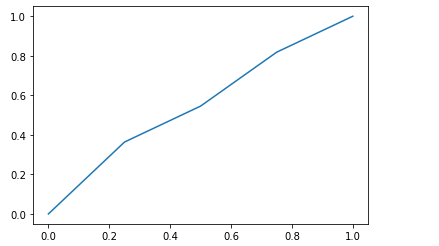
from matplotlib import pyplot as plt
import numpy as np

x = np.array([2013, 2014, 2015, 2016, 2017], dtype=np.float32)
y = np.array([12000, 14000, 15000, 16500, 17500], dtype=np.float32)

x = (x - x.min()) / (x.max() - x.min())
y = (y - y.min()) / (y.max() - y.min())

plt.plot(x, y)
plt.show()

　

最终 代码为

################### 线性回归
## 模型 y = w*x + b
## Loss = (y-y_predient)^2 = (y - w * x - b)^2
## w' = 2 * (y - w * x - b) * (-x)
## b' = 2 * (y - w * x - b) * (-1)
######### 1 numpy实现
import numpy as np
from matplotlib import pyplot as plt

x_origal = np.array([2013, 2014, 2015, 2016, 2017], dtype=np.float32)
y_origal = np.array([12000, 14000, 15000, 16500, 17500], dtype=np.float32)

x = (x_origal - x_origal.min()) / (x_origal.max() - x_origal.min())
y = (y_origal - y_origal.min()) / (y_origal.max() - y_origal.min())

loss_list = []
def loss(y, y_predict):
    loss_list.append(((y - y_predict) ** 2).sum())
#     print(loss_list)

def draw_loss():
#     print(loss_list)
    x = np.arange(len(loss_list))
    y = loss_list
    plt.plot(x, y)
    plt.show()
    
def linear_regression(x, y):
    w, b = 0, 0
    epoch = 500000
    learning_rate = 9e-4
    for i in range(epoch):
        y_predict = w * x + b
#         print(y_predict)
        loss(y, y_predict)
        w_gradient, b_gradient = 2 * (y - y_predict).dot(-x), 2 * (y - y_predict).sum() *  (-1)
#         print("w_gradient", w_gradient)
        w, b = w - learning_rate * w_gradient /len(x), b - learning_rate * b_gradient/len(x)
#         print(w, b)
    return w, b


w, b = linear_regression(x, y)
print(w, b)
print(loss_list[-1])
draw_loss()

　　画出拟合和原始线条，效果还不错

 

 

 

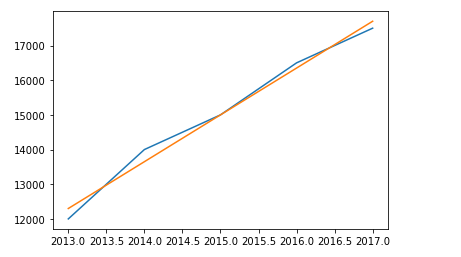
y_pre = []
for x in [2013, 2014, 2015, 2016, 2017]:
    x_std = (x - x_origal.min()) / (x_origal.max() - x_origal.min())
    y_std = w * x_std  + b
    y_pre.append(y_std * (y_origal.max() - y_origal.min()) + y_origal.min())
    
print(y_pre)
## draw
y_pre_array = np.array(y_pre)
plt.plot(x_origal, y_origal)
plt.plot(x_origal, y_pre_array)
plt.show()

　　

总结：线性回归，需要对数据进行归一化，特别是对那种画出图线 接近90度或者接近0度的，因为 这种直线拟合，比较难调整超参（学习率）进行拟合