0-回归

1、场景

　　a.根据历史的PM2.5值， 预测今天的PM2.5

       b.根据历史A股上证指数点数，预测今天的上证指数

       c.根据某个商品的销售量，预测未来一个月的销售量

2、求解方式

     2.1 建模（function set）

　　　　 y = W * X + b  表示一个线性回归 

     2.2 Loss（定义function的好坏）

　　　

     2.3 find best function

　　　 即求 W和b使得 

　　　　

 

 

 　　　求解方式一：把所有的数据集的（x,y）带入上式，然后使用线性代数偏微分等于0，可以直接求解得到w* 和 b*

　　　 求解方式二：梯度下降

        2.3.1 梯度下降

　　　　      

 

 

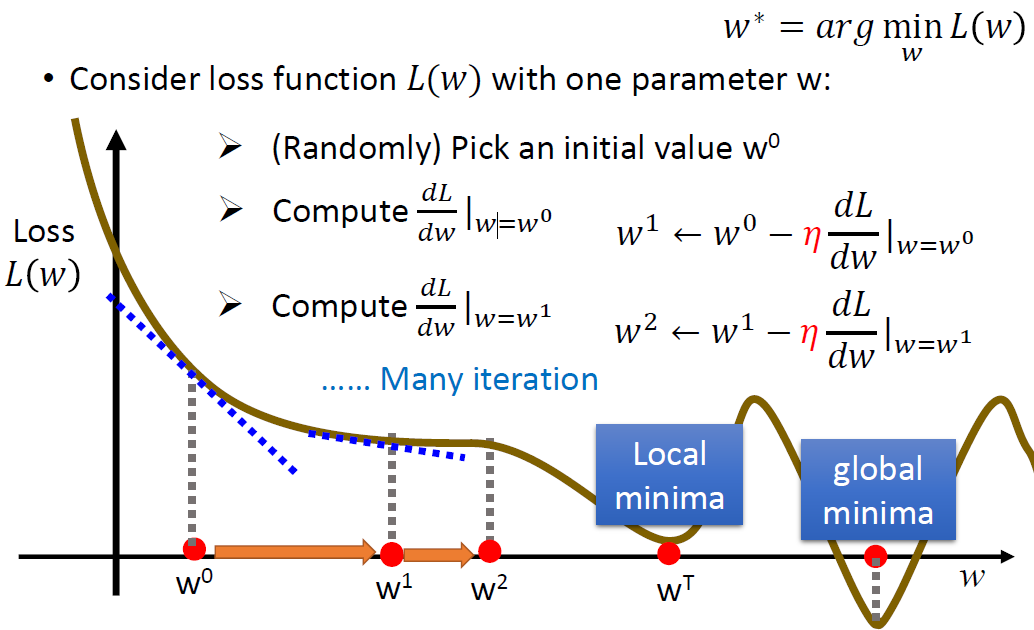
 　　　　偏导数：

　　　　　　

　　　　　　

 

 

3. 优化方向

　　3.1 修改模型

　　　　比如上述1次得模型出现如下结果：

　　

 

 

 　　　　使用2次（3次、4次）模型：y = W1 * X + W2 * X^2 + b 

    

 

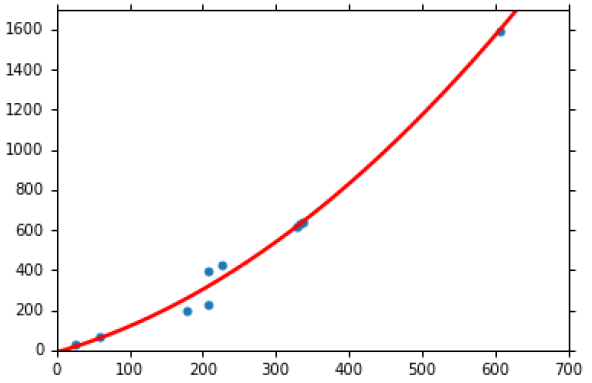
　　　　逐次增加 模型的复杂度（3次，4次，5次）画出的图如下，从下图的右下图可知，越复杂的模型包含简单的模型（模型2包含模型1，模型3包含模型2 等等），越复杂的model包含越多的function，理论是越复杂的模型能找出更好的结果，但是在test集中结果如下右图，即出现了overfitting。

                         

 

 

 　　3.2 正则

　　　　

　　　　

　　　　偏导数：

　　　　增加了后面的正则惩罚项之后，即找到的function 越小越好，又因为 y = W * X + b ，当X变化,因为w越小，所有总体function y越平滑。而function y越平滑，受到噪声（）的影响就越小。

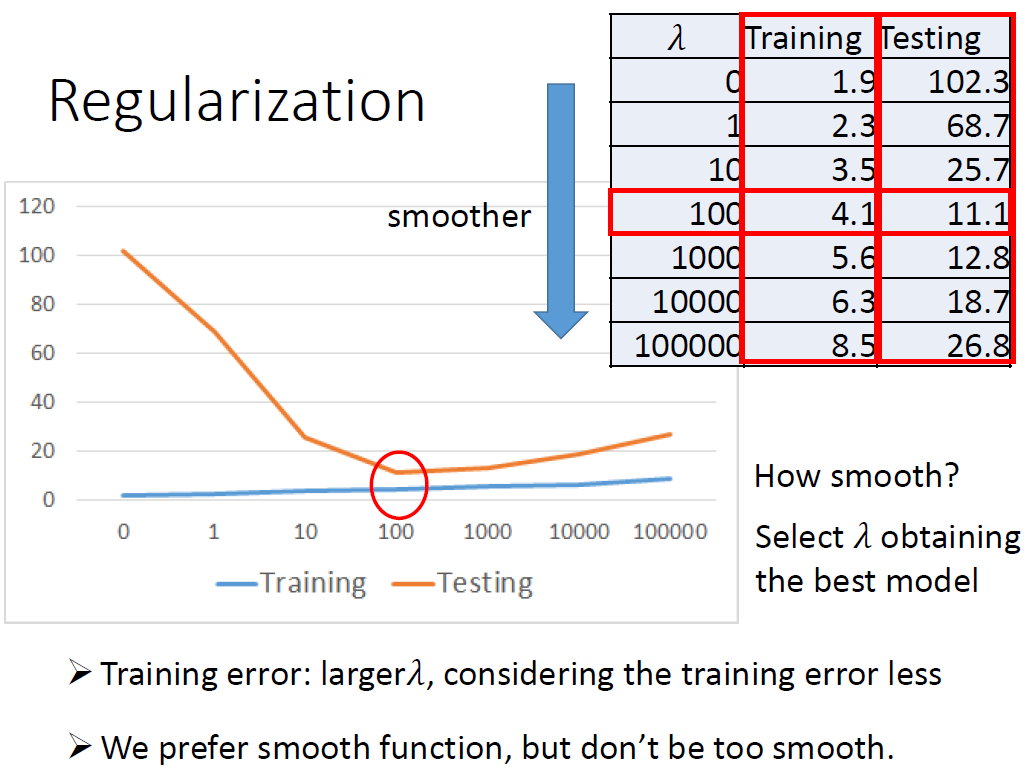
　　　　如下 调节值来调节W值，进而调节function的平滑度，有结果看出，随着值增加，function变平滑，testing效果越好。 但是当值太大。但是function太平滑了（可想象为极端情况，变成直线），效果又变差了。从这可以看出 值需作为超参进行调值，来获取最优的平滑的fucntion。

　　　　

 

 

 4、实例

　　https://www.kaggle.com/c/aia-tc-1-mid-term-exam-pm25-forecast/overview

　　利用2017/1/1~1/30數據,來預測這252台裝置在2017/1/31整天的平均PM2.5測值(by device ID)

       没有正则版本：

　　

# coding:'utf-8'
import pandas as pd
import csv
import traceback
import numpy as np

test_csv = r"D:\work\ai\hung_li_2020\1_pm2.5\test.csv"
train_csv = r"D:\work\ai\hung_li_2020\1_pm2.5\train.csv"

train_data = pd.read_csv(train_csv, encoding = 'big5')
test_data = pd.read_csv(test_csv, encoding = 'big5')

train_data = train_data.iloc[:, 3:]
print(train_data.shape)
# 处理异常数据NR
train_data[train_data == 'NR'] = 0
# pandas dataframe to numpy ndarray
raw_data = train_data.to_numpy()

# traindata为每个月前20天，所以每个月不连续，但是每个月的1-20天是连续的，所有有 12个月 * 20天 = 12 个月 * 480小时（20 * 24 小时 ）的数据，
# 每个小时有18个feature特征。按照要求 前9小时预测第10小时的PM2.5值，所以 输入特征有 12个月 * 471（480小时-9小时）小时个输入，每个输入为
# 9 * 18个特征，输出有 12个月*471个输出
month_data = {}
for month in range(12):
sample = np.empty([18, 480])
for day in range(20):
# 按月把每个月数据变成一行
sample[:, day * 24 : (day + 1) * 24] = raw_data[18 * (20 * month + day) : 18 * (20 * month + day + 1), :]
month_data[month] = sample

# 初始化好输入输出值
x = np.zeros([12 * 471, 18 * 9], dtype=float)
y = np.zeros([12 * 471, 1], dtype=float)

for month in range(12):
for day in range(20):
for hour in range(24):
if day == 19 and hour > 14:
continue
x[month * 471 + day * 24 + hour, :] = month_data[month][:,day * 24 + hour : day * 24 + hour + 9].reshape(1, -1) #vector dim:18*9 (9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9)
y[month * 471 + day * 24 + hour, 0] = month_data[month][9, day * 24 + hour + 9] #value

# nomalize data -----------------------------------------------------------------技巧1
mean_x = np.mean(x, axis = 0) #18 * 9
std_x = np.std(x, axis = 0) #18 * 9
for i in range(len(x)): #12 * 471
for j in range(len(x[0])): #18 * 9
if std_x[j] != 0:
x[i][j] = (x[i][j] - mean_x[j]) / std_x[j]

# train data and dev data
# import math
# x_train_set = x[: math.floor(len(x) * 0.8), :]
# y_train_set = y[: math.floor(len(y) * 0.8), :]
# x_validation = x[math.floor(len(x) * 0.8): , :]
# y_validation = y[math.floor(len(y) * 0.8): , :]

# train
dim = 18 * 9 + 1
w = np.zeros([dim, 1])
x = np.concatenate((np.ones([12 * 471, 1]), x), axis = 1).astype(float)
learning_rate = 100
iter_time = 1000
adagrad = np.zeros([dim, 1])
eps = 0.0000000001
for t in range(iter_time):
loss = np.sqrt(np.sum(np.power(np.dot(x, w) - y, 2))/471/12)#rmse
if(t%100==0):
print(str(t) + ":" + str(loss))
gradient = 2 * np.dot(x.transpose(), np.dot(x, w) - y) #dim*1
adagrad += gradient ** 2
w = w - learning_rate * gradient / np.sqrt(adagrad + eps)
np.save('weight.npy', w)

# predict
testdata = pd.read_csv(test_csv, header = None, encoding = 'big5')
test_data = testdata.iloc[:, 2:]
test_data[test_data == 'NR'] = 0
test_data = test_data.to_numpy()
test_x = np.empty([240, 18*9], dtype = float)
for i in range(240):
test_x[i, :] = test_data[18 * i: 18* (i + 1), :].reshape(1, -1)
for i in range(len(test_x)):
for j in range(len(test_x[0])):
if std_x[j] != 0:
test_x[i][j] = (test_x[i][j] - mean_x[j]) / std_x[j]
test_x = np.concatenate((np.ones([240, 1]), test_x), axis = 1).astype(float)
test_x