【求职面试】斐波那契数列（C#版）

经典就是经典，不论多少年，经典永远不会改变。

语言，框架总有一天会过时，但是唯独经典永远存在。这就是研究这些经典算法的永恒。

当我这样一个.net程序员去应聘Java, C++, Android岗位时，我发现框架语言特性，都被抛弃。就这样海绵一挤，我的4年水分就出来了。剩下的精华已不多。而能贯穿各个岗位的，就是这些虽在身边，但却忽视如空气般的，底层知识和应用能力。

你的经验，有多少水分呢？在一个公司久了，出来晒晒，你就发现，其实你会的并不多。

有趣问题：

1，有一段楼梯有10级台阶,规定每一步只能跨一级或两级,要登上第10级台阶有几种不同的走法?

答：这就是一个斐波那契数列：登上第一级台阶有一种登法；登上两级台阶，有一种登法；登上三级台阶，有两种登法；登上四级台阶，有三种方法……所以，1, 1，2，3，5，8，13……登上十级，有89种。

2，数列中相邻两项的前项比后项的极限是多少，就是问，当n趋于无穷大时，F(n)/F(n+1)的极限是多少？

答：这个可由它的通项公式直接得到，极限是(-1+√5)/2，这个就是所谓的黄金分割点，也是代表大自然的和谐的一个数字。

数学表示：

Fibonacci数列的数学表达式就是：

F(n) = F(n-1) + F(n-2)

F(1) = 1

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　F(2) = 1

公式是给出来了，可是为什么是这个公式呢？你有没有想过？

公式是怎么提炼出来的？我数学不好，所以我的经验就是从找规律开始：

　　如果起点是0的话，对于第一级台阶来讲有F(1)=1种走法，对于第二级来讲有F(2)=1种走法。对于第三极台阶，有1+2, 2+1两种走法。对于第四级台阶，可以从第三极台阶+1，也可以从第二级台阶+2，也就是F(4) = F(3) + F(2)，以此类推。

写代码也很简单：

        ///<summary>
        /// Fibonacci递归算法。时间复杂度O(n)=O((3/2)^n)，指数级算法
        ///</summary>
        public ulong FibonacciRecursion(int n)
        {
            if (n < 0)
                throw new ArgumentOutOfRangeException("n must > 0.");

            if (n == 1 || n == 2)
                return 1;
            return FibonacciRecursion(n - 1) + FibonacciRecursion(n - 2);
        }

那么这个超级简单的递推程序，效率是多少呢？让我们加个数组，记录每次递归的次数，同时可以output一下，看看这些有趣的数字。

        ///<summary>
        /// 递归输出Fibonacci
        ///</summary>
        public ulong FibonacciRecursionCount(int n, int[] countArray)
        {
            countArray[n]++;  //count the compute number.

            if (n < 0)
                throw new ArgumentOutOfRangeException("n must > 0.");

            if (n == 1 || n == 2)
                return 1;
            return FibonacciRecursionCount(n - 1, countArray) + FibonacciRecursionCount(n - 2, countArray);
        }

这时，可以得到每个fib(i)被计算的次数：

fib(10) = 1 fib(9) = 1 fib(8) = 2 fib(7) = 3

fib(6) = 5 fib(5) = 8 fib(4) = 13 fib(3) = 21

fib(2) = 34 fib(1) = 55 fib(0) = 34

可见，计算次数呈反向的Fibonacci数列，这显然造成了大量重复计算。

我们令T(N)为函数fib(n)的运行时间，当N>=2的时候我们分析可知：

T(N) = T(N-1) + T(N-2) + 2

而fib(n) = fib(n-1) + fib(n-2)，所以有T(N) >= fib(n)，归纳法证明可得：

fib(N) < (5/3)^N

当N>4时，fib（N）>= (3/2)^N

标准写法：

显然这个O（(3/2)^N）是以指数增长的算法，基本上是最坏的情况。

其实，这违反了递归的一个规则：合成效益法则。

合成效益法则（Compound interest rule）：在求解一个问题的同一实例的时候，切勿在不同的递归调用中做重复性的工作。

所以在上面的代码中调用fib(N-1)的时候实际上同时计算了fib(N-2)。这种小的重复计算在递归过程中就会产生巨大的运行时间。

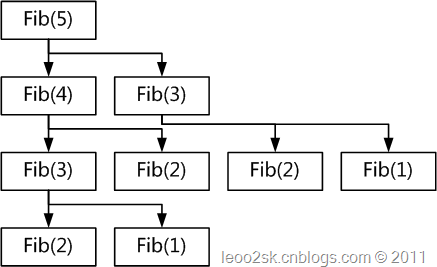
看来好看的代码未必中用，如果程序在效率不能接受那美观神马的就都是浮云了。如果简单分析一下程序的执行流，就会发现问题在哪，以计算Fibonacci(5)为例：

从上图可以看出，在计算Fib(5)的过程中，Fib(1)计算了两次、Fib(2)计算了3次，Fib(3)计算了两次，本来只需要5次计算就可以完成的任务却计算了9次。这个问题随着规模的增加会愈发凸显，以至于Fib(100)已经无法再可接受的时间内算出。

根据老赵的尾递归与Continuation 的大作，我们可以巧妙的使用尾递归算法，来实现Fibonacci：

        ///<summary>
        /// 尾递归算Fibonacci。算法时间复杂度O(n) = n
        ///</summary>
        ///<remarks>
        /// 与普通递归相比，由于尾递归的调用处于方法的最后，因此方法之前所积累下的各种状态对于递归调用结果已经没有任何意义
        /// 因此完全可以把本次方法中留在堆栈中的数据完全清除，把空间让给最后的递归调用。
        /// 这样的优化便使得递归不会在调用堆栈上产生堆积，意味着即时是“无限”递归也不会让堆栈溢出。（实际中，还是会溢出的！）
        /// 这便是尾递归的优势。
        /// 
        /// 尾递归的本质，其实是将递归方法中的需要的“所有状态”通过方法的参数传入下一次调用中。
        ///</remarks>
        public ulong FibonacciTailCall(int n, ulong sum, ulong accumulator)
        {
            if (n < 0)
                throw new ArgumentOutOfRangeException("n must > 0.");
            //n代表起点。也就是倒着算，从第n阶直到第0阶（起点）。循环n+1次。
            if (n == 0)
                return sum;   //sum是结果，初始值应该传0
            /* 传入状态：
             * 1. n每次都减一
             * 2. 传入accumulator表示把上一次的累加值当做这次的Sum
             * 3. 表示累加运算（如果是n!阶乘运算，就是* 乘法）
            */
            return FibonacciTailCall(n - 1, accumulator, sum + accumulator); 
        }

        public void TestFibonacciTailCall()
        {
            //sum初始值为0；累加器为1
            FibonacciTailCall(10, 0, 1);
        }

另：还有一种算法就是自己用Stack来模拟CLR Runtime的stack

虽然尾递归算法展现出来强大的魅力，把时间复杂度直接从指数级降到n级，但是仍然是递归算法，效率比非递归算法低。因为递归总要Stack push pop，记录一大堆指针，保存状态，垃圾回收等等。

于是我们来寻找高效的非递归算法。对于递归--非递归，最直观的是自己用Stack模拟。但是Fibonacci只需要2个运算数，因此我们没必要在Stack保存所有的中间数字，只需要保存需要计算的2个数字即可。也就是Stack.Length = 2。

        ///<summary>
        /// 使用Stack来实现Fibonacci，算法时间复杂度O(n) = n
        ///</summary>
        public ulong FibonacciStack(int n)
        {
            if (n < 0)
                throw new ArgumentOutOfRangeException("n must > 0.");

            if (n == 1 || n == 2)
                return 1;
            //只需要2个元素，用2来节省内部数组占用的内存
            Stack<ulong> stack = new Stack<ulong>(2);
            stack.Push(1);
            stack.Push(1);
            //从3开始（F(3)），直到n（F(n)）
            for (int i = 3; i <= n; i++)
            {
                var top = stack.Pop();
                var bottom = stack.Pop();
                var sum = top + bottom;
                stack.Push(top);
                stack.Push(sum);
            }
            return stack.Peek();
        }

相应的，也可以用Queue来实现。但是注意分析一些Stack和Queue实现的区别。

        ///<summary>
        /// 使用Queue来实现Fibonacci，算法时间复杂度O(n) = n
        ///</summary>
        public ulong FibonacciQueue(int n)
        {
            if (n < 0)
                throw new ArgumentOutOfRangeException("n must > 0.");

            if (n == 1 || n == 2)
                return 1;
            //只需要2个元素，用2来节省内部数组占用内存
            Queue<ulong> queue = new Queue<ulong>(2);
            queue.Enqueue(1);
            queue.Enqueue(1);
            //从3开始（F(3)），直到n（F(n)）
            for (int i = 3; i <= n; i++)
            {
                var front = queue.Dequeue();
                var end = queue.Dequeue();
                var sum = front + end;
                //为了提高效率，采用倒序queue， 也就是 8,5,3,2,1,1
                queue.Enqueue(sum);
                queue.Enqueue(front);
            }
            return queue.Peek();
        }

其实Stack和Queue都是基于数组的实现，因此对于数组还是重量级的，有了前两个的基础后，我们可以直接用数组实现。

        ///<summary>
        /// 使用数组模拟Stack来实现Fibonacci，算法时间复杂度O(n) = n
        ///</summary>
        public ulong FibonacciArray(int n)
        {
            if (n < 0)
                throw new ArgumentOutOfRangeException("n must > 0.");

            if (n == 1 || n == 2)
                return 1;

            ulong[] array = new ulong[] { 1, 1 };
            //模拟Stack结构实现
            for (int i = 3; i <= n; i++)
            {
                var sum = array[0] + array[1];
                array[0] = array[1];
                array[1] = sum;
            }
            return array[1];
        }

另外你也可以保存所有的数据，建立大数组。

        public static int CalculateFibonacciSequence(int index)
        {
            if (index <= 0)
            {
                return 0;
            }

            if (index == 1 || index == 2)
            {
                return 1;
            }

            int[] fibonacciArray = new int[index];
            fibonacciArray[0] = 1;
            fibonacciArray[1] = 1;

            for (int innerIndex = 2; innerIndex < fibonacciArray.Length; innerIndex++)
            {
                fibonacciArray[innerIndex] = fibonacciArray[innerIndex - 1] + fibonacciArray[innerIndex - 2];
            }

            return fibonacciArray[index - 1];
        }

数组已经简单了，看到这里，我们干嘛不用更轻量级的实现呢？比如2个变量。

        ///<summary>
        /// 使用变量模拟Stack来实现Fibonacci，算法时间复杂度O(n) = n
        ///</summary>
        public ulong FibonacciVariable(int n)
        {
            if (n < 0)
                throw new ArgumentOutOfRangeException("n must > 0.");

            if (n == 1 || n == 2)
                return 1;

            ulong first = 1, last = 1;
            //模拟Stack结构实现
            for (int i = 3; i <= n; i++)
            {
                //巧妙的，不借助中级变量sum
                last = first + last;
                first = last - first;
            }
            return last;
        }

有比O(n)更快的方法么？比如O(log(n))或者O(1)的？

有，当然有，首先来看看O(Log(n))的矩阵算法。摘自斐波那契数列算法分析

我们将数列写成：

Fibonacci[0] = 0，Fibonacci[1] = 1

Fibonacci[n] = Fibonacci[n-1] + Fibonacci[n-2] (n >= 2)

可以将它写成矩阵乘法形式：

将右边连续的展开就得到：

下面就是要用O(log(n))的算法计算：

显然用二分法来求，结合一些面向对象的概念，C++代码如下：

class Matrix
{

public:

       long matr[2][2]; 

       Matrix(const Matrix&rhs);

       Matrix(long a, long b, long c, long d);

       Matrix& operator=(const Matrix&);

       friend Matrix operator*(const Matrix& lhs, const Matrix& rhs)

       {

              Matrix ret(0,0,0,0);

              ret.matr[0][0] = lhs.matr[0][0]*rhs.matr[0][0] + lhs.matr[0][1]*rhs.matr[1][0];

              ret.matr[0][1] = lhs.matr[0][0]*rhs.matr[0][1] + lhs.matr[0][1]*rhs.matr[1][1];

              ret.matr[1][0] = lhs.matr[1][0]*rhs.matr[0][0] + lhs.matr[1][1]*rhs.matr[1][0];

              ret.matr[1][1] = lhs.matr[1][0]*rhs.matr[0][1] + lhs.matr[1][1]*rhs.matr[1][1];

              return ret;

       }

}; 

Matrix::Matrix(long a, long b, long c, long d)
{

       this->matr[0][0] = a;

       this->matr[0][1] = b;

       this->matr[1][0] = c;

       this->matr[1][1] = d;
}

Matrix::Matrix(const Matrix &rhs)

{

       this->matr[0][0] = rhs.matr[0][0];

       this->matr[0][1] = rhs.matr[0][1];

       this->matr[1][0] = rhs.matr[1][0];

       this->matr[1][1] = rhs.matr[1][1];

}

Matrix& Matrix::operator =(const Matrix &rhs)

{

       this->matr[0][0] = rhs.matr[0][0];

       this->matr[0][1] = rhs.matr[0][1];

       this->matr[1][0] = rhs.matr[1][0];

       this->matr[1][1] = rhs.matr[1][1];

       return *this;
} 

Matrix power(const Matrix& m, int n)
{
       if (n == 1)

              return m;

       if (n%2 == 0)

              return power(m*m, n/2);

       else

              return power(m*m, n/2) * m;
}

long fib4 (int n)

{

       Matrix matrix0(1, 1, 1, 0);

       matrix0 = power(matrix0, n-1);

       return matrix0.matr[0][0];
}

这时程序的效率为O（log(N)）。

以下内容来自维基百科

初等代数解法

已知

$a 1 = 1$
$a 2 = 1$
$a n = a n - 1 + a n - 2$

[编辑] 首先构建等比数列

设 $a n + α a n - 1 = β(a n - 1 + α a n - 2)$
化简得
$a n = (β - α) a n - 1 + αβ a n - 2$
比较系数可得:
$\begin{cases} \beta-\alpha=1 \\ \alpha\beta=1 \end{cases}$
不妨设 $β > 0,α > 0$
解得：

$\begin{cases} \alpha=\dfrac{\sqrt{5}-1}{2} \\ \beta=\dfrac{\sqrt{5}+1}{2} \end{cases}$
所以有 $a n + α a n - 1 = β(a n - 1 + α a n - 2)$ ，即 $\left\{a_n +\alpha a_{n-1}\right\}$ 为等比数列。

[编辑] 求出数列{ $a n + α a n - 1$ }

由以上可得：
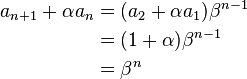
$\begin{align}a_{n+1} +\alpha a_{n} &=(a_2+\alpha a_1)\beta^{n-1}\\ & = (1+\alpha)\beta^{n-1}\\ & =\beta^n \\ \end{align}$

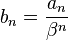
变形得： $\frac{a_{n+1}}{\beta^{n+1}}+\frac{\alpha}{\beta}\frac{a_{n}}{\beta^{n}}=\frac{1}{\beta}$ 。令 $b_n=\frac{a_n}{\beta^n}$

求数列{ $b n$ }进而得到{ $a n$ }

$b_{n+1}+\frac{\alpha}{\beta}b_{n}=\frac{1}{\beta}$
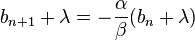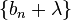设 $b_{n+1}+\lambda=-\frac{\alpha}{\beta} (b_{n}+\lambda)$ ，解得 $\lambda=-\frac{1}{\alpha+\beta}$ 。故数列 $\left\{b_n+\lambda\right\}$ 为等比数列
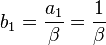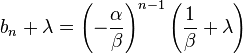
即 $b_n+\lambda=\left(-\frac{\alpha}{\beta}\right)^{n-1}\left(b_1+\lambda\right)$ 。而 $b_1=\frac{a_1}{\beta}=\frac{1}{\beta}$ ，故有 $b_n+\lambda=\left(-\frac{\alpha}{\beta}\right)^{n-1}\left(\frac{1}{\beta}+\lambda\right)$
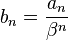
又有 $\begin{cases} \alpha=\dfrac{\sqrt{5}-1}{2} \\ \beta=\dfrac{\sqrt{5}+1}{2} \end{cases}$ 和 $b_n=\frac{a_n}{\beta^n}$
可得 $a_{n}=\frac{\sqrt{5}}{5} \cdot \left[\left(\frac{1 + \sqrt{5}}{2}\right)^{n} - \left(\frac{1 - \sqrt{5}}{2}\right)^{n}\right]$

得出 $a n$ 表达式

$a_{n}=\frac{\sqrt{5}}{5} \cdot \left[\left(\frac{1 + \sqrt{5}}{2}\right)^{n} - \left(\frac{1 - \sqrt{5}}{2}\right)^{n}\right]$

        ///<summary>
        /// 公式法。时间复杂度O(1)，但用到了计算平方根和平方运算，实际效果不一定有O(n)的好
        ///</summary>
        ///<param name="n"></param>
        ///<returns></returns>
        public ulong FibonacciFormula(int n)
        {
            if (n < 0)
                throw new ArgumentOutOfRangeException("n must > 0.");

            if (n == 1 || n == 2)
                return 1;

            double z = Math.Sqrt(5.0);
            double x = (1 + z) / 2;
            double y = (1 - z) / 2;

            double result = (Math.Pow(x, n) - Math.Pow(y, n)) / z;
            return (ulong)result;
        }

虽然ulong是默认最大的结构类型，但实际过程中，会出现溢出的问题。好在.net 4.0提供了BigInteger类。我们可以用这个类来解决溢出问题。

        ///<summary>
        /// 使用BigInteger模拟Stack来实现Fibonacci，算法时间复杂度O(n) = n
        ///</summary>
        public BigInteger FibonacciBitInteger(int n)
        {
            if (n < 0)
                throw new ArgumentOutOfRangeException("n must > 0.");

            if (n == 1 || n == 2)
                return 1;

            BigInteger first = 1, last = 1;
            for (int i = 3; i <= n; i++)
            {
                last = first + last;
                first = last - first;
            }
            return last;
        }

算法是一样的，只是BigInteger内部采用数组实现，理论上支持无限数字。

此类的使用参见：.NET 4.0 Beta2中的BigInteger和Complex类

本文参考：斐波那契数列算法分析

　　　　　　程序设计中的计算复用(Computational Reuse)

　　　　　　7种方式实现斐波那契数列

感想：

写代码没有对与错，只有精益求精。我很享受由浅入深的过程，在写文章的时候，自己也有所收获。当然，我把时间花在写文章的时候，也就丧失了其他机会。时间对于每个人都是公平的。有的人喜欢音乐，有的人喜欢看电影，而我喜欢用更好的方法来解决问题。

Enjoy your code , Enjoy your life.

posted @ 2011-10-31 17:48 primeli 阅读(3172) 评论(1) 编辑收藏举报

刷新页面返回顶部

我爱技术

淡薄名利，豁达人生，忌浮弃华，惜时珍情，寻心所向，追真求明，卧薪尝胆，造幸谋福，身心爱志，幸福人生

【求职面试】斐波那契数列（C#版）

初等代数解法

[编辑] 首先构建等比数列

[编辑] 求出数列{ $a n + α a n - 1$ }

求数列{ $b n$ }进而得到{ $a n$ }

公告

我爱技术

淡薄名利，豁达人生，忌浮弃华，惜时珍情，寻心所向，追真求明，卧薪尝胆，造幸谋福，身心爱志，幸福人生

【求职面试】斐波那契数列（C#版）

初等代数解法

[编辑] 首先构建等比数列

[编辑] 求出数列{an + αan − 1}

求数列{bn}进而得到{an}

公告

[编辑] 求出数列{ $a n + α a n - 1$ }

求数列{ $b n$ }进而得到{ $a n$ }