常见算法汇总

Hash

开放地址法，也称再散列法。

当关键字key的哈希地址p=H（key）出现冲突时，以p为基础，产生另一个哈希地址p1，如果p1仍然冲突，再以p为基础，产生另一个哈希地址p2，…，直到找出一个不冲突的哈希地址pi ，将相应元素存入其中。

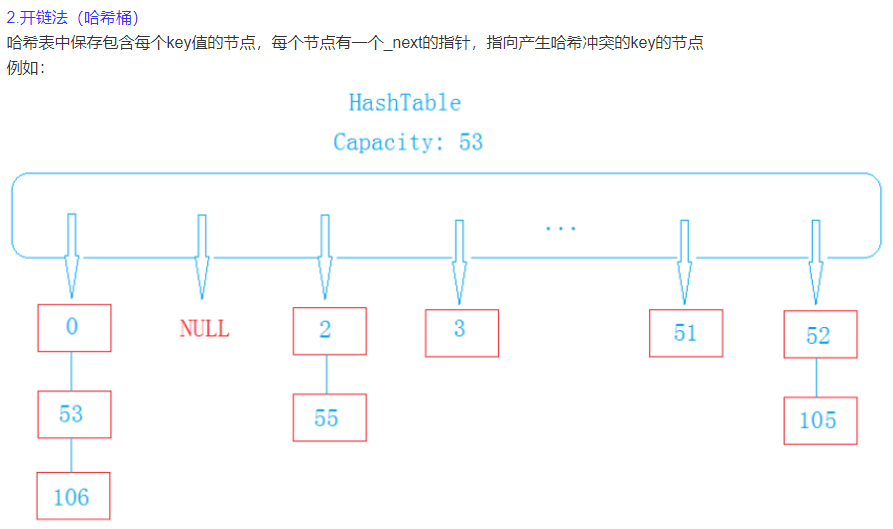
见链接： https://blog.csdn.net/xyzbaihaiping/article/details/51607770

递归

所谓递归，简单点来说，就是一个函数直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解。

比如：阶乘的实现

自己调用自己
递归通常不在意具体操作，只关心初始条件和上下层的变化关系。
递归函数需要有临界停止点，即递归不能无限制的执行下去。通常这个点为必须经过的一个数。
递归通常能被其他方案替代(栈、数组正向求)。

catalan数

catalan数卡塔兰数是组合数学中一个常在各种计数问题中出现的数列。卡塔兰数的一般公式为 C(2n,n)/(n+1)。

https://www.cnblogs.com/Morning-Glory/p/11747744.html

Dijkstra最短路径

戴克斯特拉算法使用类似广度优先搜索的方法解决赋权图的单源最短路径问题。Dijkstra 算法原始版本仅适用于找到两个顶点之间的最短路径，后来更常见的变体固定了一个顶点作为源结点然后找到该顶点到图中所有其它结点的最短路径，产生一个最短路径树。

设一个赋权有向图 $G=(V,\,E,\,W)$ 。其中的每条边 $e_{i,j}:=\left\{v_i,\,v_j\right\}$ 的权值为一个非负的实数 $w_{i,j}(e_{i,j})$ ，该权值表示从顶点 $v_i$ 到顶点 $v_j$ 的距离。并设一单源点 $s\in V$ 。现在我们的任务是：找出从源点 $s$ 出发，到 $V\setminus\{s\}$ 中所有的节点的最短路径。