BUAA ObjectOriented Unit3总结

BUAA ObjectOriented Unit3总结

目录

• BUAA ObjectOriented Unit3总结
  • 作业思路
    • 架构
    • 类图
  • 性能
    • 第九次作业
    • 第十次作业
    • 第十一次作业
    • 算法及数据结构
  • 测试
    • 自测bug
    • 自测方法
  • 评测
    • 第九次作业
    • 第十次作业
    • 第十一次作业
  • 拓展
    • 接口方法
    • JML规格
  • 心得体会与收获

​ 概括来说，本单元的任务就是在JML语言所描述的规格下维护一个社交网络系统，实现对该系统的一系列操作。单纯就难度而言，只要跟着规格说的来写就一定不会出错，从这方面来看难度确实不大，但如果完全按照规格来，一定会TLE很多点，所以要在理解规格的基础上对代码进行一些算法上的优化，不能只是单纯的照猫画虎。（其实这也从某一方面说明了写代码和写规格是两件完全不同的事情）

作业思路

架构

• 由于本单元基本上已经给你搭建好了架构层次，只需要你完成这些层次中的代码，所以只需要严格按照官方包中所说的来，它叫你实现那些接口就实现相应的接口，唯一值得说的就是第三次作业中MyRedEnvelopeMessage，MyNoticeMessage，MyEmojiMessage类，不仅要实现官方包中对应的接口，还需要继承MyMessage类（否则会有大片的复制粘贴）
• 除了按照官方包所构建的架构层次实现相应接口外，还需要建立一些其他的类用来放置用于优化的数据结构类，比如说边表的节点Edge，并查集UnionFind
• 至于容器的选择，Person中的Messages因为要按顺序插入读取，采用了LinkList，其他都是用的HashSet和HashMap（HashMap的key值为id，value为类的引用），使用HashMap是为了通过id快速得到相应类的引用，否则如果只需要进行遍历之类的操作，就使用HashSet，这样下来大部分的操作均为\(O(1)\)
• 关于构建的图模型及维护策略，实际上就是一边读取一边动态处理，把读取到的元素储存在合适的容器中，使用高效的数据结构进行维护，同时还可以把一些要查询的信息提前算出来，而不是等到要查询的时候再计算。

类图

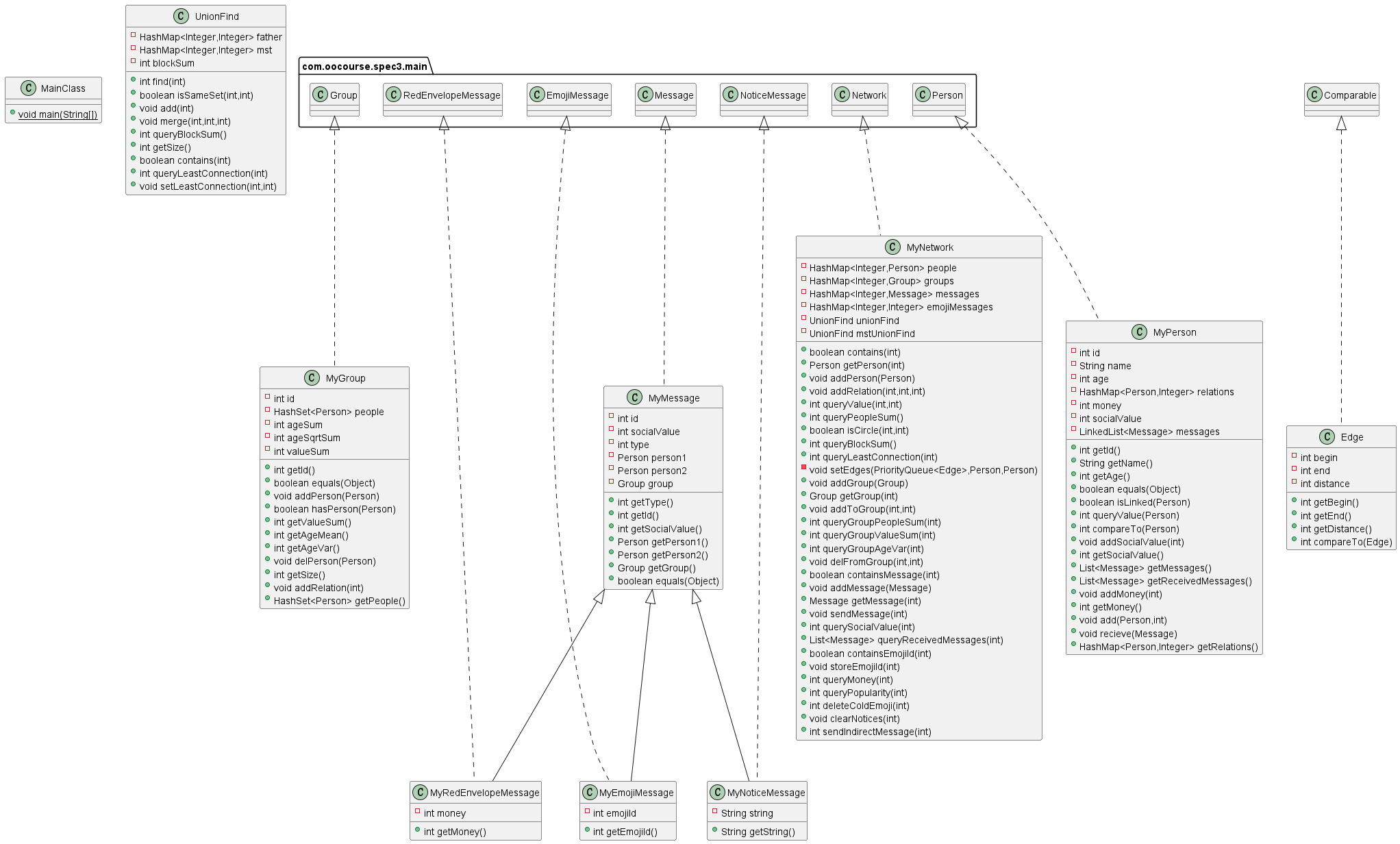
性能

第九次作业

• query_circle(qci):通过并查集维护连通分量，从而直接查询，能够得到均摊\(O(1)\)的复杂度，同时加入路径压缩，最坏情况下复杂度为\(O(mlogn)\)，平均复杂度为\(O(mα(m,n))\)，在使用路径压缩的基础上，只能加上按质量合并，无法加入按秩合并，但在我实际用较大数据测下来发现，其实只要用路径压缩就好了，其他的不会更快
• query_block_sum(qbs)：在使用并查集维护连通分量的同时，还可以维护一个变量用于记录连通分量的个数，能够得到\(O(1)\)复杂度，而如果严格按规格写，则至少是\(O(n^2)\)的复杂度

第十次作业

• query_group_value_sum(qgvs):在加人删人以及添加关系时候动态维护，能够得到\(O(1)\)复杂度

• query_group_age_var(qgav):同样在加人删人时候动态维护 Group内所有人的年龄和以及年龄平方和，利用如下公式，能够得到\(O(1)\)复杂度：

  \[Var=\frac{∑x^2−2×mean×∑x+n×mean^2}n \]

• query_least_connection(qlc):求查询人所处联通分量中的最小生成树大小，以关系 value为边权，主流的算法有两种，分别是Kruskal和Prim：

  • Kruskal：使用\(O(mlogm)\)的排序算法以及复杂度为\(O(mα(m,n))\)或者\(O(mlogn)\)的并查集，总的时间复杂度为\(O(mlogm)\)
  • Prim：一般采用堆优化后的Prim算法，复杂度为\(O((n+m)logn)\)，主要由两部分组成，首先是取出堆顶最小的点将其中一个端点加入集合\(U\)中\(O(nlogn)\)，然后是更新\(U\)到集合外点的最小距离集合，复杂度为\(O(mlogn)\)

  而我实际上在写作时，两种方法都使用了，在我对比后发现Kruskal比Prim更快一点，这是存图方式的问题，图存在哪呢？存在了每个Person类中，你可以从Person类得到与其相邻的点以及该边的权值，这样看来，你还得把信息提取出来，区别就在这了

  写的时候，我一直在想，能不能和实现qgvs和qgav时一样，对最小生成树进行动态维护呢？答案是可以的，但我没用，为啥呢，因为违背了这门课不是要让我们卷算法的初衷（因为我不会啊），但我又想更快一点，于是就想出了一个行之有效的优化——缓存最小生成树：

  众所周知，最小生成树只有在有指令 ar的时候才有可能改变，同时求一个 Person的最小生成树等价于求并查集中它的父节点的最小生成树，于是，可以开一个 HashMap<Person, Integer> 储存每个 fa以及它的最小生成树大小，同时还需要记录该最小生成树是否有效，而 ar操作分为两种，一种是在一个连通分量内部加关系，一种是在两个连通分量间加关系，而在两个联通分量之间添加关系时，直接将它们的 fa缓存的最小生成树相加，再加上该关系的 value，然后将该值更新为新联通分量（两个连通分量合并而得）中fa的最小生成树即可，如果是第一种情况，就记录一下该值无效即可，等着之后计算，而在之后计算中，也要更新下缓存，这样同一个连通分量的最小生成树只要算一次了，这是我写的对拍机跑出来的对比：

  ----- TEST CASE 1 BEGIN -----
  TIME
  sjh used : 11.8783847s
  tlb used : 7.9584311s
  RESULT
  All answers are identical
  ------ TEST CASE 1 END ------
  
  
  ----- TEST CASE 2 BEGIN -----
  TIME
  sjh used : 12.9031707s
  tlb used : 8.3050189s
  RESULT
  All answers are identical
  ------ TEST CASE 2 END ------
  
  
  ----- TEST CASE 3 BEGIN -----
  TIME
  sjh used : 12.1142242s
  tlb used : 8.1749079s
  RESULT
  All answers are identical
  ------ TEST CASE 3 END ------
  
  
  ----- TEST CASE 4 BEGIN -----
  TIME
  sjh used : 13.9344497s
  tlb used : 8.6737702s
  RESULT
  All answers are identical
  ------ TEST CASE 4 END ------
  

  在非常大的数据下，缓存快了非常多

第十一次作业

• send_indirect_message(sim)：在一个连通分量中发送两个人之间消息时，计算这两个人之间的最短路，不二之选\(Dijkstra\)：
  • \(Dijkstra\)：不使用任何数据结构进行维护，每次松弛操作执行完毕后，直接在\(S\)集合中暴力寻找最短路长度最小的结点\(O(n^2)\)。松弛操作总时间复杂度为\(O(m)\)，故全过程的时间复杂度为\(O(n^2+m)=O(n^2)\) 。如果使用二叉堆进行优化，插入（修改）和删除的时间复杂度均为\(O(logn)\) ，时间复杂度为\(O((n+m)logn)=O(mlogn)\)。

算法及数据结构

这里只放出自己写的最小生成树缓存的部分代码（其他代码在网上都有板子）

• \(UnionFind\)（包含了最小生成树的缓存）：

  public class UnionFind {
      private final HashMap<Integer, Integer> father = new HashMap<>();
      private final HashMap<Integer, Integer> mst = new HashMap<>();
  
      public UnionFind() {
      }
  
      public int find(int id) {
          return father.get(id) == id ? id : father.merge(id, find(father.get(id)), (a, b) -> b);
      }
  
      public void add(int id) {
          father.put(id, id);
          mst.put(id, 0);
      }
  
      public void merge(int id1, int id2, int value) {
          int i = find(id1);
          int j = find(id2);
          if (i == j) {
              mst.put(i, -1);//-1代表该最小生成树的缓存无效
              return;
          }
          father.put(i, j);
          if (mst.get(i) != -1 && mst.get(j) != -1) {
              mst.merge(j, mst.get(i) + value, Integer::sum);
          } else {
              mst.put(j, -1);
          }
      }
  }
  

• \(Kruskal\)（Edge是自己写的一个类）：

  public int queryLeastConnection(int id) throws PersonIdNotFoundException {
      if (!people.containsKey(id)) {
          throw new MyPersonIdNotFoundException(id);
      } else {
          //这里是通过缓存得到值
          if (unionFind.queryLeastConnection(id) != -1) {
              return unionFind.queryLeastConnection(id);
          }
          //这里是通过Kruskal算出值
          mstUnionFind = new UnionFind();
          PriorityQueue<Edge> edges = new PriorityQueue<>();
          setEdges();//do something
          int totalDistance = 0;
          while () {
  			//do something
          }
          unionFind.setLeastConnection(id, totalDistance);//算后也更新下缓存
          return totalDistance;
      }
  }
  

测试

自测bug

qgav的精度有问题，具体如下：

\[Var=\frac{∑x^2−2×mean×∑x+n×mean^2}n \]

但是如果写成：

\[Var=\frac{∑x^2−2×mean×∑x}n+mean^2 \]

就会出现精度错误，原因在于 Java计算整数除法时会省略小数部分，这点在正数和负数下都是直接丢，所以既不是向上取整也不是向下取整

自测方法

舍友hys写了三次作业的数据生成器和一个简易的对拍机，我优化了他的对拍机的时间测量方法，使得时间测量更准确可信（程序运行时间测不准是个很大的毛病，PyCharm的终端无法测准，我花了很长时间才找到比较好的方法）

'''
				PARAMETER
	src_list: 储存jar包名字的列表，无需后缀.jar
	num: 第num组数据
	time_limit: 运行时限

				TIPS 
	需要提前将生成的数据存储在input.txt中
'''
def test(src_list: list, num: int, time_limit: float) -> None:
    print('----- TEST CASE ' + str(num) + ' BEGIN -----')
    print('           TIME')
    for src in src_list:
        os.environ["COMSPEC"] = 'powershell'
        p = subprocess.Popen(
            'Measure-Command{Get-Content input.txt | java -jar ' + src + '.jar > ' + src + '.txt}',
            shell=True, stdout=subprocess.PIPE)
        p.wait()
        time_list = p.stdout.read()
        sorted_list = time_list.decode('utf-8').strip().split('\n')
        time_used = float(sorted_list[9].split(": ")[1])
        print(src + ' used : ' + str(time_used) + 's')
        if time_used >= time_limit:
            print(src + ' is TLE')
            os.system('pause')
    print('          RESULT')
    pre = src_list[0]
    for i in range(1, len(src_list)):
        os.system('fc ' + pre + '.txt ' + src_list[i] + '.txt /n > result.txt')
        result = open('result.txt', 'r')
        result.readline()
        if 'FC' not in result.readline():
            print(src_list[i] + ' is different with ' + pre)
            os.system('pause')
        pre = src_list[i]
    print('  All answers are identical')
    print('------ TEST CASE ' + str(num) + ' END ------\n\n')

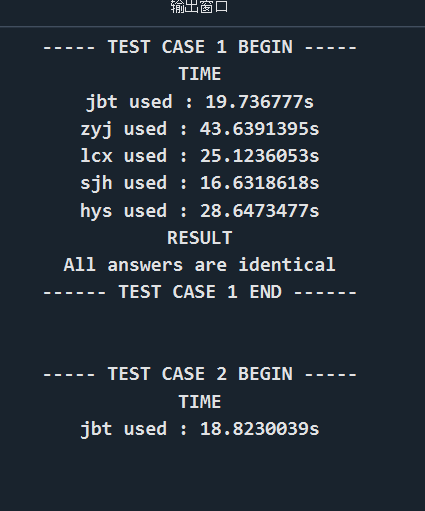
之后我还写了图形化界面，并将其包装成了软件，具体效果如下：

评测

本单元强测互测均未出 bug，关于它人的 bug：

第九次作业

• qbs次数过多时 TLE，原因在于没有在维护并查集的同时，维护连通块数量，有的人甚至没有用并查集

第十次作业

• 没找到

第十一次作业

• 没找到

拓展

接口方法

Advertiser，Producer，Customer都可以设计为Person子接口，BuyingMessage，AdertiseMessage可以设计为Message的子接口

• Advertiser：各种get方法
• Producer：各种get方法
• Customer：各种get方法
• MyNetWork：
  • get，add，contains等基本方法
  • queryProductSales：查询对应ProducerId的产品的销售额
  • queryProductPath：查询ProducerId的产品的所有销售路径
  • buyProduct:Customer在发送成功对应BuyingMessage后可以买东西
  • sendBuyingMessage:Customer向Advertiser发送购买需求，或者是向Produce发送Advertiser持有的BuyingMessage
  • sendAdvertiseMessage:Advertiser向Customer发送广告
• 异常接口

JML规格

• sendAdvertiseMessage：

  /*@ public nomal_behavior
      @ requires containsMessage(id) && (getMessage(id) instance of AdvertiseMessage) && getMessage(id).getType() == 0 &&
      @          getMessage(id).getPerson1().isLinked(getMessage(id).getPerson2()) &&
      @          getMessage(id).getPerson1() != getMessage(id).getPerson2();
      @ assignable messages;
      @ assignable getMessage(id).getPerson2().messages;
      @ assignable getMessage(id).getPerson1().socialValue, getMessage(id).getPerson2().socialValue;
      @ ensures !containsMessage(id) && messages.length == \old(messages.length) - 1 &&
      @         (\forall int i; 0 <= i && i < \old(messages.length) && \old(messages[i].getId()) != id;
      @         (\exists int j; 0 <= j && j < messages.length; messages[j].equals(\old(messages[i]))));
      @ ensures \old(getMessage(id)).getPerson1().getSocialValue() ==
      @         \old(getMessage(id).getPerson1().getSocialValue()) + \old(getMessage(id)).getSocialValue() &&
      @         \old(getMessage(id)).getPerson2().getSocialValue() ==
      @         \old(getMessage(id).getPerson2().getSocialValue()) + \old(getMessage(id)).getSocialValue();
      @ ensures (\forall int i; 0 <= i && i < \old(getMessage(id).getPerson2().getMessages().size());
      @          \old(getMessage(id)).getPerson2().getMessages().get(i+1) == \old(getMessage(id).getPerson2().getMessages().get(i)));
      @ ensures \old(getMessage(id)).getPerson2().getMessages().get(0).equals(\old(getMessage(id)));
      @ ensures \old(getMessage(id)).getPerson2().getMessages().size() == \old(getMessage(id).getPerson2().getMessages().size()) + 1;
      @ also
      @ public normal_behavior
      @ requires containsMessage(id) && (getMessage(id) instance of AdvertiseMessage) && getMessage(id).getType() == 1 &&
      @           getMessage(id).getGroup().hasPerson(getMessage(id).getPerson1());
      @ assignable people[*].socialValue, messages;
      @ ensures !containsMessage(id) && messages.length == \old(messages.length) - 1 &&
      @         (\forall int i; 0 <= i && i < \old(messages.length) && \old(messages[i].getId()) != id;
      @         (\exists int j; 0 <= j && j < messages.length; messages[j].equals(\old(messages[i]))));
      @ ensures (\forall Person p; \old(getMessage(id)).getGroup().hasPerson(p); p.getSocialValue() ==
      @         \old(p.getSocialValue()) + \old(getMessage(id)).getSocialValue());
      @ ensures (\forall int i; 0 <= i && i < people.length && !\old(getMessage(id)).getGroup().hasPerson(people[i]);
      @          \old(people[i].getSocialValue()) == people[i].getSocialValue());
      @ also
      @ public exceptional_behavior
      @ signals (MessageIdNotFoundException e) !containsMessage(id);
      @ signals (NotAdvertiseMessageException e) containsMessage(id) && !(getMessage(id) instance of AdvertiseMessage);
      @ signals (RelationNotFoundException e) containsMessage(id) && (getMessage(id) instance of AdvertiseMessage) &&
      @          getMessage(id).getType() == 0 && !(getMessage(id).getPerson1().isLinked(getMessage(id).getPerson2()));
      @ signals (PersonIdNotFoundException e) containsMessage(id) && (getMessage(id) instance of AdvertiseMessage) &&
      @          getMessage(id).getType() == 0 && !(getMessage(id).getGroup().hasPerson(getMessage(id).getPerson1()));
      @*/
  

• queryProductSales：

  /*@ public normal_behavior
    @ requires containsProducer(id);
    @ assignable \nothing;
    @ ensures \result == getProducer(id).sales;
    @ also
    @ public exceptional_behavior
    @ signals (ProducerIdNotFoundException e) !containsProducer(id1));
    @*/
  

• buyProduct：

  /*@ public normal_behavior
    @ requires (containsCustomer(id1) && containsProducer(id2) && num > 0 && ReadyToBuy(id1, id2));
    @ assignable getProducer(id2).sales, containsCustomer(id1).money;
    @ ensures getProducer(id2).sales == \old(getProducer(id2).sales) + getProducer(id2).productPrice * num;
    @ ensures getCustomer(id1).money == \old(getCustomer(id1).money) - getProducer(id1).productPrice * num;
    @ ensures \result == true;
    @ also
    @ public normal_behavior
    @ requires (containsCustomer(id1) && containsProducer(id2) && num < 0 && && ReadyToBuy(id1, id2));
    @ assignable \nothing;
    @ ensures \result == false;
    @ also
    @ public exceptional_behavior
    @ signals (CustomerIdNotFoundException e) !containsCustomer(id1));
    @ signals (ProducerIdNotFoundException e) (containsCustomer(id1) && !containsProducer(id2));
    @ signals (ProducerNotReadyToBuyException e) (containsCustomer(id1) && containsProducer(id2) && !ReadyToBuy(id1, id2));
    @*/
  

心得体会与收获

• 单纯就难度而言，只要跟着规格说的来写就一定不会出错，从这方面来看难度确实不大，但如果完全按照规格来，一定会TLE很多点，所以要在理解规格的基础上对代码进行一些算法上的优化，不能只是单纯的照猫画虎。（其实这也从某一方面说明了写代码和写规格是两件完全不同的事情）
• 第一次接触JML语言，还是不太熟悉，看懂都要好久，很多都是结合着方法名猜意思的
• 花了很多时间想优化问题，收获了一些优化心得
• 写了对拍机，之后的\(jar\)包都能用来对拍了