动态规划-0-1背包
0-1背包,动态规划解决方案
三个物品, 考虑背包能够携带的重量只有5 。对于这个例子,我们可以说最佳解决方案是往背包里装入
物品1 和物品2 ,这样,总重量为5 ,总价值为7 。

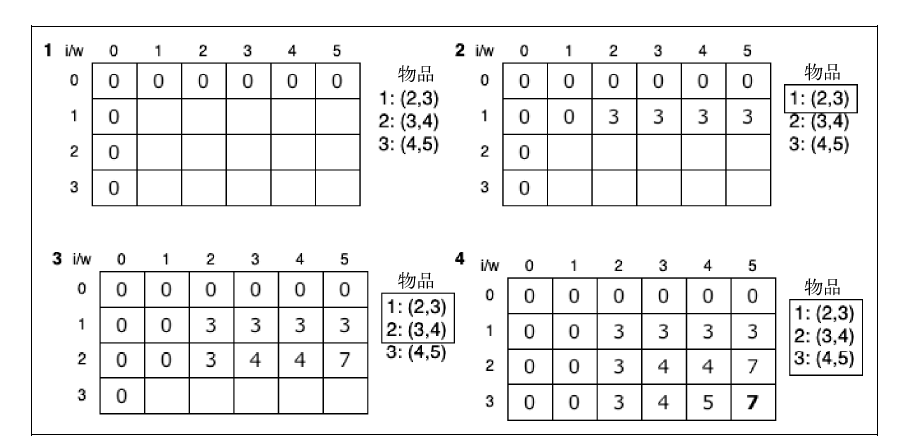
function knapSack(capacity, weights, values, n) { var i, w, a, b, kS = []; for (i = 0; i <= n; i++) { //{1}首先,初始化将用于寻找解决方案的矩阵ks[n+1][capacity+1] kS[i] = []; } for (i = 0; i <= n; i++) { for (w = 0; w <= capacity; w++) { if (i == 0 || w == 0) { //{2}忽略矩阵的第一列和第一行,只处理索引不为0的列和行 kS[i][w] = 0; } else if (weights[i - 1] <= w) { //{3}物品i的重量必须小于约束(capacity)才有可能成为解决方案的一部分;否则, //总重量就会超出背包能够携带的重量,这是不可能发生的。发生这种情况时,只要忽略 //它,用之前的值就可以了(行{5})。 a = values[i - 1] + kS[i - 1][w - weights[i - 1]]; b = kS[i - 1][w]; kS[i][w] = (a > b) ? a : b; //{4} max(a,b) 当找到可以构成解决方案的物品时,选择价值最大的那个 } else { kS[i][w] = kS[i - 1][w]; //{5} 最后,问题的解决方案就在这个二维表格右下角的最后一个格子里 } } } findValues(n, capacity, kS, weights, values); return kS[n][capacity]; //{6} } function findValues(n, capacity, kS, weights, values) { var i = n, k = capacity; console.log('解决方案包含以下物品:'); while (i > 0 && k > 0) { if (kS[i][k] !== kS[i - 1][k]) { console.log('物品' + i + ',重量:' + weights[i - 1] + ',价值:' + values[i - 1]); i--; k = k - kS[i][k]; } else { i--; } } } var values = [3, 4, 5], weights = [2, 3, 4], capacity = 5, n = values.length; console.log(knapSack(capacity, weights, values, n)); //输出 7



 浙公网安备 33010602011771号
浙公网安备 33010602011771号