啦啦啦啦啦啦啦啦啦
啦啦啦
啦啦啦啦啦啦啦啦啦
转载
前 30 分钟通读题目:快速浏览所有题目,标记难度等级和预估得分,优先选择有把握的题目开始作答,避免因卡题浪费时间。
分阶段把控进度:
第 1 小时:完成简单题或部分分代码框架,确保基础分数;
第 2-3 小时:集中攻克中等难度题目,优化代码逻辑;
最后 1 小时:检查已写代码,完善注释和边界条件处理,冲刺难题部分分;
ABC221G
神秘题,将坐标轴转 \(45°\),然后 bitset 优化背包,记录路径把刚刚被更新的找出来,然后 _Find_next,每个点只会记一次。
AGC050a
神秘题,想到 \(\log\),然后发现一下位置 \(x\) 走十次能到的区间是 \([1024x,1024x+1023]\),区间长度够,每次直接连 \((2x,2x+1)\),超出去的对 \(n\) 取模。
魔法少女网站
Ynoi,思路是对操作分块,每 \(B\) 次修改分一块,块内的询问按 \(x\) 排序,询问的其实是关于所有 \(\le x\) 形成连续段的二次函数。
对于一次询问,把 \(\le x\) 的看成 \(1\),每个点维护连续段左右端点,序列分块先插入所有与修改无关的点,因为询问排过序所以每个点只会被加入一次。
剩下和修改有关的点每次暴力跑 \(B\) 次修改,注意上述数据结构不支持删除,所以每次要暴力撤销。
常数爆炸,注意到每个点记录的连续段左右端点只会有一个,所以可以压成一个数组,还有基数排序等等卡常技巧。
最后还是过不去后面的点,拼了个暴力过了????
暴力过 Ynoi
Amusement Park
学习子集反演:
本题考虑 dp,\(f(S)\) 表示点集 \(S\) 的导出子图不成环的方案数。
枚举一圈入度为 \(0\) 的点,也就是这些点在原图上形成独立集。
考虑枚举独立集,可以预处理,然后容斥。考虑容斥系数是啥。
令 \(g(S)\) 在全集 \(Q\) 中为度数为 \(0\) 的集合恰好为 \(S\) 的方案数,\(h(S)\) 为钦定度数为 \(0\) 的集合为 \(S\) 的方案数,即:
\(w(T)\) 表示 \(T\) 是否是独立集。根据子集反演:
然后就做完了。
学习一个枚举子集的小技巧:
for(int i=1;i<(1<<n);i++)
for(int j=i;j;j=i&(j-1))
Desant
再看还是没思路啊。
注意到数据范围,枚举子集,\(f(i,S)\) 表示枚举到 \(i\) 位,选的集合为 \(S\) 的答案。
直接记录状态就是 \(2^n\) 的,因为我们要转移,所以需要记录值域的状态。
但是后面没有选的元素只有 \(n-i\) 个,选的数会形成若干个连续段,我们只关心每个连续段分别选了多少个数就可以了。
所以处理出连续段,然后 hash 起来作为状态,\(f(i,S)\) 第一位可以滚掉,可以证明 \(|S|\) 不会超过 \(3^{\frac{n}{3}}\):
即 \(\sum x_i =n\),求 \(\prod x_i\) 最大值,根据均值不等式 \(x_i = x\) 时最优,所以求 \(x^{\frac{n}{x}}\) 的最值,取个 \(\ln\) 变成 \(n \frac{\ln x}{x}\),求个导变成 \(n \frac{1 - \ln x}{x^2}\),所以在 \(x=\mathrm{e}\) 取到最值。取整就是 \(3^{\frac{n}{3}}\)。
转移时枚举区间和,然后合并区间。
小清新人渣的本愿
由乃的玉米田
图很炸裂。
很水啊,乘法枚举因数就是 \(\sqrt{n}\) 的,加和减直接上 bitset 就行。
除法也很好做,上面已经确定是根号或者 bitset 的算法了。
考虑根号分治,大于 \(B\) 的一共只有 \(\frac{V}{B}\) 个倍数,直接枚举,
小于 \(B\) 的一共只有 \(B\) 个,对于每个数预处理 \(x\) 倍出现的前一个和后一个位置,用个线段树维护一下区间交然后判断区间是否包含。为啥不用 ST 表?空间开不下。
最后因为空间问题,\(B\) 取到 \(64\) 就行,复杂度和 bitset 一样。
游走
XOR和路径
若干年前欠下的高斯消元,省选前来学一下。
两道题看起来差不多,但是感觉不太一样。
第一道是板子,答案就是每条边期望经过次数,发现边的不太好直接算,先算点的,然后就能知道边期望次数了。
第二道先拆位,有效边被走次数为奇数就有贡献,还想这样做,发现毫无办法知道边经过奇数次的概率,那么就直接记从 \(u\) 到 \(n\) 经过奇数次有效边的概率,转移:
然后就做完了。
放个高消的板子。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 65;
#define double long double
const double eps = 1e-18;
int n;
double a[N][N],ans[N];
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n+1;j++)
{
scanf("%Lf",&a[i][j]);
}
}
for(int j=1;j<=n;j++)
{
int t=0;
for(int i=1;i<=n;i++)
if((i>=j||fabs(a[i][i])<=eps)&&fabs(a[i][j])>fabs(a[t][j])) t=i;
if(!t) continue;
for(int k=1;k<=n+1;k++) swap(a[j][k],a[t][k]);
for(int i=1;i<=n;i++) if(i!=j)
{
double t=a[i][j]/a[j][j];
for(int k=1;k<=n+1;k++) a[i][k]-=t*a[j][k];
}
}
bool no=0,oo=0;
for(int i=1;i<=n;i++)
{
if(fabs(a[i][i])>eps) ans[i]=a[i][n+1]/a[i][i];
else if(fabs(a[i][n+1])>eps) {no=1;}// 判无解
else {oo=1;}// 无穷解
if(fabs(ans[i])<eps) ans[i]=0;
}
if(no) printf("-1\n");
else if(oo) printf("0\n");
else
{
for(int i=1;i<=n;i++) printf("x%d=%.2Lf\n",i,ans[i]);
}
return 0;
}
MUL-Multidrink
超级大模拟.话说现在怎么人均场切黑了!!
当然思路也很难想啦,容易发现叶子是特殊的,而且从 \(1\) 到 \(n\) 的链也是特殊的。
先把根链拿出来,根链外的子树必须形如一条链上挂若干个叶子,否则不可能跳回来。
先考虑这部分怎么做,先把这条链拿出来,然后隔一个遍历,途中把上一个节点的叶子收了。(如图)
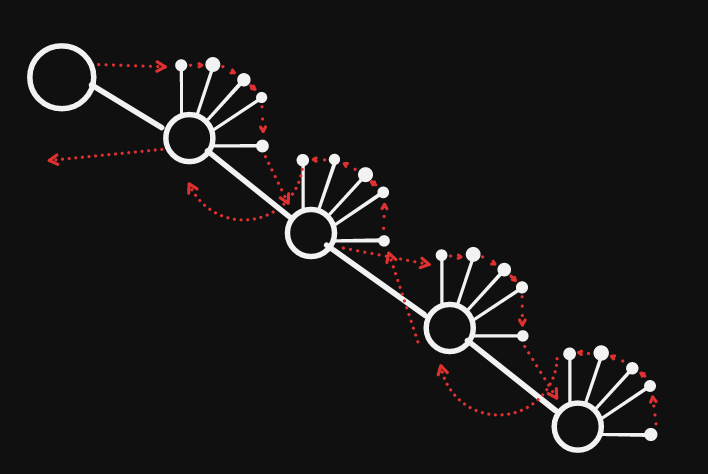
忽视叶子,对于每一个有一棵子树的根链上的节点都这样跑,如果没有那它可以直接跳到下一个节点,帮助下一个节点跑一棵子树。
贪心策略就是这样。
划分
长度为 \(n+m\) 的 \(01\) 串,划分成两个长度分别为 \(n,m\) 的序列,得到两个二进制数使其和最大。
贪心,最终目的就是使 \(1\) 尽量靠前,考虑先得到一个方案然后交换,限制就是 \(01\) 顺序和原串一致。
令 \(n \ge m\),我们想让 \(1\) 尽量靠前,要拿 \(m\) 串的 \(1\) 去替换 \(n\) 串里靠前的 \(0\)。
所以反过来先将 \(m\) 串填满,然后每次交换就相当于将 \(0/1\) 整体平移。
Easy Problem
长度 \(3n\) 的序列选出长度 \(3k\) 的子序列,使 \(\sum_{i=1}^{k} median(a_{p_{3i-2}},a_{p_{3i-1}},a_{p_{3i}})\) 最大,对于每个 \(k\) 求解。
暴力:\(n^2\log n\) 预处理每个区间的次大数,状态 \(f_{i,j}\) 在前 \(i\) 位里选 \(j\) 个的最大值。转移 \(f_{i,j}=max_{k=0}^{i-1} f_{k,j-1}+w(k+1,i)\),复杂度 \(n^3\)。
考虑优化,发现毫无前途。
考虑每个数的贡献,只要这个区间内有比它大的和比它小的那么就有贡献,单调栈找到前一个比它大的、小的,后一个比它大的、小的。贡献位置有本身的位置,后一个大、小的出现位置,扫描线 dp。
Trash Problem
暴力就能过,但是暴力都不会。
\(n^2\) 枚举左上角,然后从左往右做扫描线,复杂度 \(O(\frac{n^4}{\omega})\)。
具体扫描时确定下界,对于每一列,两个一组,记录上面那个的位置。
第一个下界是无法两个一组匹配了,第二个是和上一列拼完剩下无法匹配的位置成为下界。实现时记录不能作为下界的位置。
Minimum Cost Paths P
看到平方想差分!!!
对于每一列来说,每两个的差值都是 \(c_y\)。
转移到下一列,如果横着走过去,那么差值会增加 \(2x-1\),如果从上面过去,差值就变成 \(c_{y+1}\) 了。
前者是一条斜线,后者是平台,最终得到的差分就是单调不降的。
每次进行后缀推平,用栈记,然后连续一段就是横着走的,段与段之间是向下走的,记录每一段开头的位置和值,可以计算。
扫描线。
大概长这样。
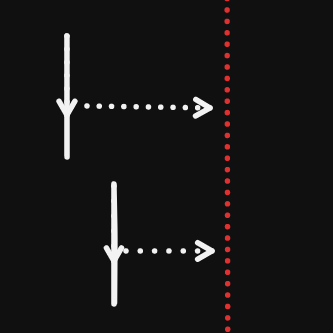
Counting Triangles 2
赛时怎么也没想到那个边长为 \(\sqrt{5}\) 的三角形。。。
暴力:枚举每个点,列式子求另外一个点的范围,即转 \(90°\) 后还在范围内,注意特判自己。
玄学解法,按暴力打表,发现有规律,做两次二维差分,就做完了。
Build the Tower
玄学。
因为这道题去学了高消,但是和高消没关系。
令 \(f_{S}\) 表示栈状态为 \(S\) 时最终的答案。
发现这是个类似树上的问题,转移由儿子和父亲转移过来。
考虑边界
观察到最后那个式子表示我们可以用父亲表示儿子,可以写成如下形式:
首先处理状态,注意到这个东西只和子树有关,也就是我们不关心退栈操作了,所以状态只需要记录栈顶元素和权值和。
然后递归上去带回就能求出每一个点和其父亲的关系。
最终答案没有父亲,所以答案就是 \(B_{0}\)
茎
把根链单拿出来做 dp,其他子树跑背包。
根链从 \(u\) 转移到 \(v\) 枚举有多少点在 \(v\) 被砍掉之后被选,这个就是任意选的后缀和。
还是做背包。
CF204E
给定一个字符串序列 \(s_i\),定义一个“好串” \(t\) 当且仅当这个串在不少于 \(k\) 个字符串中出现过,问每个串 \(s_i\) 的子串中“好串”的数量。
复习 SA。
首先把所有 \(s_i\) 拼起来,中间用分隔符隔开,那么每个子串就是每一个后缀的前缀。
在多少个字符串出现过可以二分 ST 表加主席树区间数颜色做。
注意到如果一个大的串合法,那么它的子串也是合法的,这个也可以二分。
复杂度 \(O(n \log^2 n)\)。
ARC189D
单调栈,发现一个小的如果能在若干步后合并一个大的,那么反过来大的一定能合并小的,答案是一样的。
所以并查集,将小的答案指向它能合并的大的上,注意相等情况需要特判。
ARC187B
若干年前感觉超级困难的题,现在能自己做了。
过了发现才只是蓝。深深的感到自己的弱小。
发现每一个连通块一定都是一个区间。
考虑连通块内最大的元素,一个前面的点和它没有连边当且仅当前缀最小值大于它,同理考虑最小的元素和后面没有连边当且仅当后缀最大值大于它。
所以问题变成区间计数,考虑贡献记在左端点,即每个点有多少种方案作为左端点。
枚举前缀最小值,可以容斥一下,然后就能确定后缀最大值的范围。
IZLET
对于相邻且同种颜色的点可以直接缩,剩下的发现一下,只在路径颜色数为 \(2\) 的两个点之间连边跑生成树就是对的。
同颜色直接缩应该是没问题的,为什么任意一棵生成树就是对的?
考虑把有两种颜色交替的路径拿出来,会形成一个团,我们其实并不关心这个团内部的结构,只要它是颜色交替,并且和外面的边的连接是正确的就行。
同样,团与团之间的顺序也是不关心的。
三分
哈哈,刚学会三分,每次取 \(mid-eps,mid+eps\) 作为 \(lmid,rmid\),删掉一半。
有平台不可以。
ARC191C
太困难了!
如果没有最小解要求,容易想到 \(A = n+1,M = n\),但这不保证最小解。
然后神奇想到 \((n+1)^n-1\) 最后一项是 \(\binom{n}{1} n = n^2\),如果令 \(M = n^2\),那么能保证最小解。
ARC189B
感觉很困难啊。
如果想到差分就好说了,其实就是交换 \(p,p+2\),然后排序,注意特判 \(n=2\)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号