省选集训
AGC018C
好像挺典的,贪心 trick。
三维限制,首先容易想到全分配给一号,然后往出取,变成从 \(n\) 个物品中取 \(v_2\) 个给二号,\(v_3\) 个给三号,贡献变成差值。
然后就变成 CF730I。
考虑贪心,临项交换法,假如放进一号的贡献为 \(a\),放进二号的贡献为 \(b\)。
假如两个物品 \(i,j\) 都放进去,且 \(i\) 放一号 \(j\) 放二号比 \(i\) 放二号 \(j\) 放一号优,那么有:
交换得到:
因此我们按 \(a-b\) 排序,那么存在一个分界点,使前缀中选了所有放进二号的,后缀中选了所有放进一号的。
优先队列可以预处理前缀中选 \(v\) 个物品的最大值,同理后缀也可以。统计答案即可。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 1e5+5;
int n,v[3],c[N];
LL ans,a[N][3],f[N];
priority_queue<LL> q;
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
for(int i=0;i<3;i++) scanf("%d",&v[i]),n+=v[i];
for(int i=1;i<=n;i++) for(int j=0;j<3;j++) scanf("%lld",&a[i][j]);
for(int i=1;i<=n;i++)
{
ans+=a[i][2]; c[i]=i;
a[i][1]-=a[i][2]; a[i][0]-=a[i][2];
}
sort(c+1,c+1+n,[&](const int &x,const int &y){return a[x][1]-a[x][0]<a[y][1]-a[y][0];});
LL now=0;
for(int i=1;i<=n;i++)
{
if(i<=v[0]) q.push(-a[c[i]][0]),now+=a[c[i]][0];
else
{
LL tmp=a[c[i]][0]+q.top();
if(tmp>0) q.pop(),q.push(-a[c[i]][0]),now+=tmp;
}
if(i>=v[0]) f[i]=now;
}
while(!q.empty()) q.pop();
now=0; LL res=-1e18;
for(int i=n;i>=1;i--)
{
if(n-i+1<=v[1]) q.push(-a[c[i]][1]),now+=a[c[i]][1];
else
{
LL tmp=a[c[i]][1]+q.top();
if(tmp>0) q.pop(),q.push(-a[c[i]][1]),now+=tmp;
}
if(n-i+1>=v[1]&&i-1>=v[0]) res=max(res,f[i-1]+now);
}
printf("%lld\n",ans+res);
return 0;
}
AGC032E
还是贪心。人类智慧?
从小到大排序,所有匹配对可以分为两类:\(\lt m\) 的和 \(\ge m\) 的。
对于同一类,显然存在包含关系时最优(最大的和最小的、次大的和次小的...)。
对于不同类的,可以证明并列关系最优(大分讨)。
所以一定有一个分界点,使前缀中只有第一类,后缀中只有第二类。
显然,分界点越靠右越优,二分可解。
场上真的需要证明贪心吗?
code
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+5;
int n,a[N],m;
inline bool check(int mid)
{
for(int l=mid+1,r=n;l<r;l++,r--)
{
if(a[l]+a[r]<m) return 0;
}
return 1;
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d",&n,&m);n<<=1;
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
sort(a+1,a+1+n);
int l=0,r=n,res=1;
while(l<=r)
{
int mid=l+r>>1;
if(check(mid)) r=mid-1,res=mid;
else l=mid+1;
}
if(res&1) res++;
int ans=0;
for(int i=1,j=res;i<j;i++,j--)
ans=max(ans,(a[i]+a[j]));
for(int i=res+1,j=n;i<j;i++,j--)
ans=max(ans,(a[i]+a[j])-m);
printf("%d\n",ans);
return 0;
}
[JSOI2007] 建筑抢修
朴素贪心。
按截止时间排序。
先能选就选,选不了考虑能不能替换之前的。
如果能使总花费时间变小的话一定不劣,所以开堆记一下之前的最大值。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 1.5e5+5;
int n;
struct A {int x,y;} a[N];
priority_queue<int> q;
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d%d",&a[i].x,&a[i].y);
sort(a+1,a+1+n,[&](const A &x,const A &y){return x.y<y.y;});
LL sum=0; int ans=0;
for(int i=1;i<=n;i++)
{
int tmp=q.top();
if(sum+a[i].x<=a[i].y) sum+=a[i].x,q.push(a[i].x),ans++;
else if(tmp>a[i].x) q.pop(),sum+=a[i].x-tmp,q.push(a[i].x);
}
printf("%d\n",ans);
return 0;
}
最短路

\(n\) 年以前的题。
由于最短路唯一,想到建最短路树(如果不唯一不一定是树)。
断掉树边,加一条连向子树外的非树边,新的贡献就是 \(d_v+w\),发现对于每一条边 \(v_i=d_u+d_v+w\) 是一定的,对点 \(u\) 的贡献可以由 \(v_i-d_u\) 得到。
按 \(v_i\) 从小到大加入边,中间可以用并查集维护已更新过得点,复杂度近似 \(O(n)\)。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5,M = 2e5+5;
#define LL long long
int n,m;
int head[N],tot;
struct E {int u,v,w;} e[M<<1],ed[M<<1];
inline void add(int u,int v,int w) {e[++tot]={head[u],v,w}; head[u]=tot;}
LL d[N],ans[N];
bool vs[N];
int dep[N],f[N],fa[N];
inline int find(int x) {return fa[x]==x?(x):(fa[x]=find(fa[x]));}
inline void dj(int s)
{
priority_queue<pair<LL,int> > q;
memset(ans,0x3f,sizeof(ans));
memset(d,0x3f,sizeof(d));
d[s]=0; q.push({0,s});
while(!q.empty())
{
int u=q.top().second; q.pop();
if(vs[u]) continue;
vs[u]=1;
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v;
if(!vs[v]&&d[v]>d[u]+e[i].w)
{
d[v]=d[u]+e[i].w; dep[v]=dep[u]+1; f[v]=u;
q.push({-d[v],v});
}
}
}
}
inline void work(int x,int y,LL w)
{
while(x!=y)
{
if(dep[x]<dep[y]) swap(x,y);
ans[x]=min(ans[x],w-d[x]);
fa[find(x)]=find(f[x]);
x=find(f[x]);
}
}
int main()
{
freopen("path.in","r",stdin);
freopen("path.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) fa[i]=i;
for(int i=1;i<=m;i++)
{
int x,y,z; scanf("%d%d%d",&x,&y,&z);
add(x,y,z); add(y,x,z); ed[i]={x,y,z};
}
dj(1);
sort(ed+1,ed+1+m,[&](const E &x,const E &y){return d[x.u]+d[x.v]+x.w<d[y.u]+d[y.v]+y.w;});
for(int i=1;i<=m;i++)
{
int u=ed[i].u,v=ed[i].v,w=ed[i].w;
if(d[u]==d[v]+w||d[v]==d[u]+w) continue;
work(u,v,d[u]+d[v]+w);
}
for(int i=2;i<=n;i++) printf("%lld\n",ans[i]>=1e11?(-1):(ans[i]));
return 0;
}
购物

感觉自己当年能想到还是挺牛的。
假如选所有物品,\(s=\sum a_i\),\(k\) 的范围显然是 \([\lceil \frac{s}{2} \rceil ,s]\)
将所有物品从小到大排序,考虑删去最小的物品后 \(s\) 仍大于等于 \(\lceil \frac{s}{2} \rceil\),
因此重复上述操作能得到一个连续的区间,\([\lceil \frac{ a_{max} }{2}\rceil,s]\)。
这是一开始选择所有物品,要想扩大区间发现只和最大值有关,每次删去最大值即可,复杂度 \(O(n)\)。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 1e5+5;
int n,a[N];
LL sum,ans;
int main()
{
freopen("buy.in","r",stdin);
freopen("buy.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]),sum+=a[i];
sort(a+1,a+1+n);
LL l,r=sum,L=r+1,R;
for(int i=n;i>=1;i--)
{
l=ceil((1.0*a[i]/2));
R=min(r,L-1); L=max(l,1ll);
ans+=R-L+1;
r-=a[i];
}
printf("%lld\n",ans);
return 0;
}
TEST_100
trick,值域折叠。
处理绝对值问题常用方法。注意到绝对值实际上可以转化为两点间距离。
而距离对称点距离相同的两点完全等价。
假设一开始有 \(x\),进行一次操作就是 \(|x-a_i|\),也就是 \(x\) 到 \(a_i\) 的距离,考虑对原点进行操作。
原来 \(a_i\) 的位置 \(|x-a_i|=0\),因此让距离 \(x\) 为 \(a_i\) 的点做新的原点,只考虑操作后原点在有效值域上(不在就不用操作了)。
然后根据对称点完全等价的性质将较小的一半对折过去,用并查集维护即可。
实际上和 回收 Bot 是一样的。
code
#include<bits/stdc++.h>
using namespace std;
bool MB;
const int N = 1e5+5,M = 350;
int n,m,a[N],S,cnt,bl[N],L[M],R[M],mx;
int fa[N],d[M][N];
inline int find(int x) {return fa[x]==x?(x):(fa[x]=find(fa[x]));}
inline int que(int l,int r,int v)
{
int s=bl[l],e=bl[r],res=v;
if(s>=e-1) {for(int i=l;i<=r;i++) res=(res-a[i]>=0?(res-a[i]):(a[i]-res));}
else
{
for(int i=l;i<=R[s];i++) res=(res-a[i]>=0?(res-a[i]):(a[i]-res));
for(int i=s+1;i<=e-1;i++) res=d[i][res];
for(int i=L[e];i<=r;i++) res=(res-a[i]>=0?(res-a[i]):(a[i]-res));
}
return res;
}
inline int read()
{
int res=0; char x=getchar();
while(x<'0'||x>'9') x=getchar();
while(x<='9'&&x>='0') res=(res<<1)+(res<<3)+(x^48),x=getchar();
return res;
}
bool MP;
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
// cerr<<(&MB-&MP)/1048576.0;
scanf("%d%d",&n,&m); S=min<int>(sqrt(n)+100,n); cnt=n/S;
for(int i=1;i<=n;i++) a[i]=read();
for(int i=1;i<=cnt;i++) L[i]=R[i-1]+1,R[i]=R[i-1]+S; R[cnt]=n;
for(int i=1;i<=cnt;i++)
{
int l=0,r=N-5,k=0;
for(int j=l;j<=r;j++) fa[j]=j;
for(int j=L[i];j<=R[i];j++)
{
bl[j]=i;
if(k<=l) k+=a[j]; else k-=a[j];
if(k>=l&&k<=r)
{
if(k-l<=r-k)
{
for(int h=l;h<k;h++) fa[h]=(k<<1)-h;
l=k;
}
else
{
for(int h=k+1;h<=r;h++) fa[h]=(k<<1)-h;
r=k;
}
}
}
for(int j=0;j<=N-5;j++) d[i][j]=abs(k-find(j));
}
int ans=0;
while(m--)
{
int l=read(),r=read(),v=read();
l^=ans; r^=ans; v^=ans;
ans=que(l,r,v);
printf("%d\n",ans);
}
return 0;
}
CF702F
平衡树好题。
学习 插入-标记-回收 维护函数复合。
显然这是一个分段函数复合问题。
按上述方法,我们将查询作为节点插入数据结构中。然后通过打标记的方式进行修改。
本题显然比较好做直接做。
FHQ 维护子树减,子树加即可。发现子树减之后需要进行平衡树有交合并。
可以按类似归并的方法,每次找出两棵树中最小的一段,然后依次加入新树。
复杂度为 \(O(n\log^2 n)\),证明用到势能函数,详见 平衡树有交合并复杂度证明。
另一种解释是复杂度正确性是基于本题性质:
假如要减去的数是 \(c\),那么两棵树可以分裂成 \([0,c),[c,2c),[2c,\infty)\),有交的只有中间一段。
并且对于中间这段,每次操作会使其整体除二,那么最多进行 \(log\) 次操作。
实现时直接 \(log\) 查最小值比维护子树最小值要快,问?
code
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+5;
int n,m,ans[N];
struct A {int a,b;} a[N];
namespace FHQ
{
struct D {int x,id,ans;} va[N];
int rt,tot,pr[N],sz[N],tag[N],son[N][2],ta[N];
inline void pushup(int k) {sz[k]=sz[son[k][0]]+sz[son[k][1]]+1;}
inline void add(int k,int x) {va[k].x+=x; tag[k]+=x;}
inline void ad(int k,int x) {va[k].ans+=x; ta[k]+=x;}
inline void pushdown(int k)
{
if(tag[k])
{
int lz=tag[k]; tag[k]=0;
add(son[k][0],lz); add(son[k][1],lz);
}
if(ta[k])
{
int lz=ta[k]; ta[k]=0;
ad(son[k][0],lz); ad(son[k][1],lz);
}
}
inline int merge(int x,int y)
{
if(!x||!y) return x|y;
if(pr[x]<=pr[y]) return pushdown(x),son[x][1]=merge(son[x][1],y),pushup(x),x;
else return pushdown(y),son[y][0]=merge(x,son[y][0]),pushup(y),y;
}
inline void split(int rt,int &x,int &y,int k)
{
if(!rt) return x=y=0,void(0);
pushdown(rt);
if(va[rt].x<=k) x=rt,split(son[x][1],son[x][1],y,k);
else y=rt,split(son[y][0],x,son[y][0],k);
pushup(rt);
}
inline int kth(int rt,int k)
{
pushdown(rt);
if(sz[son[rt][0]]>=k) return kth(son[rt][0],k);
if(sz[son[rt][0]]+1==k) return va[rt].x;
return kth(son[rt][1],k-sz[son[rt][0]]-1);
}
inline int nw(D x) {va[++tot]=x; sz[tot]=1; tag[tot]=ta[tot]=0; pr[tot]=rand(); return tot;}
inline void ins(D k)
{
int x,y; split(rt,x,y,k.x);
rt=merge(merge(x,nw(k)),y);
}
inline void debug(int rt)
{
if(!rt) return;
pushdown(rt);
debug(son[rt][0]); debug(son[rt][1]);
}
inline void mdf(int k)
{
int x,y,z; split(rt,x,y,k-1);
add(y,-k); ad(y,1); rt=0;
while(sz[x]&&sz[y])
{
int tmp1=kth(x,1),tmp2=kth(y,1);
if(tmp1<=tmp2) split(x,z,x,tmp2);
else split(y,z,y,tmp1);
rt=merge(rt,z);
}
if(sz[x]) rt=merge(rt,x);
if(sz[y]) rt=merge(rt,y);
}
} using namespace FHQ;
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d%d",&a[i].a,&a[i].b);
sort(a+1,a+1+n,[&](const A &x,const A &y){return x.b==y.b?(x.a<y.a):(x.b>y.b);});
scanf("%d",&m);
for(int i=1,x;i<=m;i++) scanf("%d",&x),ins({x,i,0});
for(int i=1;i<=n;i++) mdf(a[i].a); debug(rt);
for(int i=1;i<=tot;i++) ans[va[i].id]=va[i].ans;
for(int i=1;i<=m;i++) printf("%d ",ans[i]);
return 0;
}
排队
仍然是 插入-标记-回收 维护函数复合。
平衡树直接做。但是线段树也可以。
注意到对于所有询问按左端点排序,那么任意时刻已加入的查询一定是单调的(不考虑右端点)。
所以我们可以对于询问开线段树,插入询问就在线段树最右面找一个点,然后映射回来。
通过线段树二分可以找到中间的合法区间,然后区间加。
比平衡树要简单的多。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+5;
int n,m,ans[N],cnt,ys[N];
struct A {int l,r;} a[N];
struct Q {bool v; int id;};
vector<Q> q[N];
namespace SEG
{
struct T {int mx,mi,lz;} tr[N<<2];
inline void pushup(int k) {tr[k].mi=min(tr[k<<1].mi,tr[k<<1|1].mi); tr[k].mx=max(tr[k<<1].mx,tr[k<<1|1].mx);}
inline void pushdown(int k)
{
if(tr[k].lz)
{
int lz=tr[k].lz; tr[k].lz=0;
tr[k<<1].mi+=lz; tr[k<<1].mx+=lz; tr[k<<1].lz+=lz;
tr[k<<1|1].mi+=lz; tr[k<<1|1].mx+=lz; tr[k<<1|1].lz+=lz;
}
}
inline void mdf(int k,int l,int r,int L,int R,int v)
{
if(l>=L&&r<=R)
{
tr[k].mi+=v; tr[k].mx+=v; tr[k].lz+=v;
return;
}
pushdown(k);
int mid=l+r>>1;
if(L<=mid) mdf(k<<1,l,mid,L,R,v);
if(R>mid) mdf(k<<1|1,mid+1,r,L,R,v);
pushup(k);
}
inline int getl(int k,int l,int r,int L,int R,int v)
{
if(l>=L&&r<=R)
{
if(tr[k].mx<v) return -1;
if(l==r) return l;
}
pushdown(k);
int mid=l+r>>1;
if(L<=mid&&tr[k<<1].mx>=v)
{
int res=getl(k<<1,l,mid,L,R,v);
if(res!=-1) return res;
}
if(R>mid&&tr[k<<1|1].mx>=v) return getl(k<<1|1,mid+1,r,L,R,v);
return -1;
}
inline int getr(int k,int l,int r,int L,int R,int v)
{
if(l>=L&&r<=R)
{
if(tr[k].mi>v) return -1;
if(l==r) return l;
}
pushdown(k);
int mid=l+r>>1;
if(R>mid&&tr[k<<1|1].mi<=v)
{
int res=getr(k<<1|1,mid+1,r,L,R,v);
if(res!=-1) return res;
}
if(L<=mid&&tr[k<<1].mi<=v) return getr(k<<1,l,mid,L,R,v);
return -1;
}
inline int que(int k,int l,int r,int p)
{
if(l==r) return tr[k].mx;
pushdown(k);
int mid=l+r>>1;
if(p<=mid) return que(k<<1,l,mid,p);
else return que(k<<1|1,mid+1,r,p);
}
} using namespace SEG;
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d%d",&a[i].l,&a[i].r);
for(int i=1;i<=m;i++)
{
int l,r; scanf("%d%d",&l,&r);
q[l].push_back({0,i}); q[r+1].push_back({1,i});
} cnt=m+1;
for(int i=1;i<=n+1;i++)
{
for(auto &x:q[i])
{
if(x.v) ans[x.id]=que(1,1,m,ys[x.id]);
else ys[x.id]=--cnt;
}
if(i==n+1) break;
int l=getl(1,1,m,cnt,m,a[i].l),r=getr(1,1,m,cnt,m,a[i].r);
if(l!=-1&&r!=-1) mdf(1,1,m,l,r,1);
}
for(int i=1;i<=m;i++) printf("%d\n",ans[i]);
return 0;
}
interval
给定 个区间,你需要求出能够最多选出多少对区间,使得两个区间不交。要求
一个区间最多属于一对选出的区间。
还是贪心,可反悔。
按左端点排序后,由于左端点递增,右端点越靠左越优。
对于之前匹配过的 \(a,b\) 区间 和当前枚举到的 \(c\),如果 \(b\) 的右端点比 \(c\) 靠左,那么必然可以用 \(c\) 替换 \(b\)(注意这里为什么能想到根据右端点反悔)。
根据右端点靠左更优,替换必然更优。剩下 \(b\)。
当然如果能选剩下的先直接选。
赛时完全假的图的匹配加上随机化骗了 \(60pts\),但是离散化挂了一点,幸亏没卡。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5+5;
int n;
int tl[N<<1],tot,mt[N];
struct A
{
int l,r,id;
inline bool operator < (const A &x) const
{
return r>x.r;
}
} a[N];
unordered_map<int,int> mp;
inline int read()
{
int res=0; char x=getchar();
while(x<'0'||x>'9') x=getchar();
while(x<='9'&&x>='0') res=(res<<1)+(res<<3)+(x^48),x=getchar();
return res;
}
bool vs[N];
priority_queue<A> q1,q2;
mt19937 rd(time(0));
int main()
{
// freopen("interval.in","r",stdin);
// freopen("interval.out","w",stdout);
n=read();
for(int i=1;i<=n;i++) a[i].l=read(),a[i].r=read(),tl[++tot]=a[i].l,tl[++tot]=a[i].r;
sort(tl+1,tl+1+tot);
tot=unique(tl+1,tl+1+tot)-tl-1;
for(int i=1;i<=tot;i++) mp[tl[i]]=i;
for(int i=1;i<=n;i++) a[i].l=mp[a[i].l],a[i].r=mp[a[i].r];
sort(a+1,a+1+n,[&](const A &x,const A &y){return x.l<y.l;});
int ans=0;
for(int i=1;i<=n;i++)
{
a[i].id=i;
bool fl=0;
if(!q1.empty())
{
auto x=q1.top();
if(x.r<a[i].l)
{
q1.pop(); fl=1; ans++;
mt[x.id]=i; mt[i]=x.id;
q2.push(a[i]);
}
}
if(!fl&&!q2.empty())
{
auto x=q2.top();
if(x.r<a[i].r)
{
q2.pop(); fl=1;
mt[i]=mt[x.id]; mt[mt[x.id]]=i; mt[x.id]=0;
q1.push(x);
q2.push(a[i]);
}
}
if(!fl) q1.push(a[i]);
}
printf("%d\n",ans);
return 0;
}
the soldier of love
中级扫描线。
如果只有一个点。
考虑点能被哪些区间贡献。
很多个点也这样做,但是会有重的。
所以微调一下扫描线范围,使扫描区间不交。
code
#include<cstdio>
#include<vector>
#include<unordered_map>
#include<algorithm>
using namespace std;
const int N = 1e6+5;
int n,m,tl[N],tot,ans[N];
struct A {int l,r;} a[N];
struct Q {int id,l,r;};
vector<int> v[N],d[N];
vector<Q> q[N];
unordered_map<int,int> mp;
namespace BIT
{
int c[N];
inline void mdf(int x,int v) {for(;x<=tot;x+=(x&-x)) c[x]+=v;}
inline int que(int x) {int res=0; for(;x;x-=(x&-x)) res+=c[x]; return res;}
} using namespace BIT;
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
while(scanf("%d%d",&n,&m)!=EOF)
{
tot=0; mp.clear();
for(int i=1;i<=n;i++) scanf("%d%d",&a[i].l,&a[i].r),tl[++tot]=a[i].l,tl[++tot]=a[i].r;
for(int i=1;i<=m;i++)
{
int c; scanf("%d",&c);
for(int j=1,x;j<=c;j++) scanf("%d",&x),v[i].push_back(x),tl[++tot]=x;
v[i].push_back(1e9);
}
tl[++tot]=1e9;
sort(tl+1,tl+1+tot);
tot=unique(tl+1,tl+1+tot)-tl-1;
for(int i=1;i<=tot;i++) mp[tl[i]]=i;
for(int i=1;i<=n;i++) d[mp[a[i]+30.
.l]].push_back(mp[a[i].r]);
for(int i=1;i<=m;i++)
{
v[i][0]=mp[v[i][0]];
for(int j=0;j<v[i].size()-1;j++) v[i][j+1]=mp[v[i][j+1]],q[v[i][j]].push_back({i,v[i][j],v[i][j+1]-1});
}
for(int i=1;i<=tot;i++)
{
for(int &x:d[i]) mdf(x,1);
for(Q &x:q[i]) ans[x.id]+=(que(x.r)-que(x.l-1));
}
for(int i=1;i<=m;i++) printf("%d\n",ans[i]),ans[i]=0,v[i].clear();
for(int i=1;i<=tot;i++) q[i].clear(),d[i].clear(),c[i]=0;
}
return 0;
}
A.数据结构
高级扫描线。
正难则反,考虑一个数 \(x\) 什么时候不会出现。
只有所有 \(x\) 都被加一,并且所有 \(x-1\) 都没有被加一。
前者可以记录最左和最右端点,是一个区间,后者可以记录 \(x-1\) 的出现位置,没有出现的也是若干区间。
然后小分讨,细节略多。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+5;
int n,m,a[N],l[N],r[N],lst[N],ans[N],sum;
struct D {int l,r,v;};
vector<D> d[N];
struct Q {int id,r;};
vector<Q> q[N];
namespace BIT
{
int c[N];
inline void mdf(int x,int v) {for(;x<=n;x+=(x&-x)) c[x]+=v;}
inline int que(int x) {int res=0; for(;x;x-=(x&-x)) res+=c[x]; return res;}
} using namespace BIT;
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=n+1;i++) l[i]=n+2;
for(int i=1;i<=n;i++) scanf("%d",&a[i]),l[a[i]]=min(l[a[i]],i),r[a[i]]=max(r[a[i]],i);
for(int i=1;i<=n;i++)
{
int l=lst[a[i]]+1,r=i-1;
lst[a[i]]=i;
if(l>r) continue;
if(!::r[a[i]+1])
{
d[l].push_back({l,r,-1}); d[r+1].push_back({l,r,1});
continue;
}
if(l>r||!(l<=::l[a[i]+1]&&r>=::r[a[i]+1])) continue;
int L=min(r,::l[a[i]+1]),R=max(::r[a[i]+1],l);
d[l].push_back({R,r,-1}); d[L+1].push_back({R,r,1});
}
for(int i=0;i<=n;i++) if(!r[i])
{
int l=1,r=n;
if(!::r[i+1])
{
d[l].push_back({l,r,-1}); d[r+1].push_back({l,r,1});
continue;
}
if(!(l<=::l[i+1]&&r>=::r[i+1])) continue;
int L=min(r,::l[i+1]),R=max(::r[i+1],l);
d[l].push_back({R,r,-1}); d[L+1].push_back({R,r,1});
}
else
{
int l=lst[i]+1,r=n;
if(l>r) continue;
if(!::r[i+1])
{
d[l].push_back({l,r,-1}); d[r+1].push_back({l,r,1});
continue;
}
if(l>r||!(l<=::l[i+1]&&r>=::r[i+1])) continue;
int L=min(r,::l[i+1]),R=max(::r[i+1],l);
d[l].push_back({R,r,-1}); d[L+1].push_back({R,r,1});
}
for(int i=1;i<=m;i++)
{
int x,y; scanf("%d%d",&x,&y);
q[x].push_back({i,y});
}
for(int i=1;i<=n;i++)
{
for(auto &x:d[i]) mdf(x.l,x.v),mdf(x.r+1,-x.v);
for(auto &x:q[i]) ans[x.id]+=que(x.r);
}
for(int i=1;i<=m;i++) printf("%d\n",ans[i]+n+1);
return 0;
}
对数据结构的爱
神秘数据结构。
出发点应该是 \(p\) 是固定的,我们可以记录减了多少个 \(p\)。一个长度为 \(len\) 的区间最多减 \(len\) 个 \(p\)。
每减一个 \(p\) 对应的初始值都是一段区间,我们只需要记录这个端点,然后线段树维护分段函数,就能在 \(O(q\log^2 n)\) 查询。
但是合并两端区间看起来是 \(O(???)\) 的,不太行。
发现一点性质,区间左端点一定是单增的。同理,对于左子树减 \(x\) 的最小值所对应的柚子树的减 \(y\) 的值是单增的。
所以双指针可以做到 \(O(n\log n)\) 预处理。
有点抽象。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 1e6+1,M = 2e5+1;
const LL inf = 1e16;
int n,m,a[N],p;
namespace SEG
{
LL sum[N<<1]; int sz[N<<1];
vector<LL> tr[N<<1];
inline void pushup(const int k,const int mid)
{
sum[k]=sum[mid<<1]+sum[mid<<1|1]; LL ttt=sum[mid<<1];
const int ls=sz[mid<<1],rs=sz[mid<<1|1];
for(int l=0,r=0;l<=ls;++l)
{
const LL tmp=tr[mid<<1][l+1]-1+ttt-1ll*l*p,tt=tr[mid<<1][l];
if(r==rs+1) r--;
for(;r<=rs;++r)
{
if(tmp<tr[mid<<1|1][r]) {r--; break;}
tr[k][l+r]=min(tr[k][l+r],max(tr[mid<<1][l],tr[mid<<1|1][r]-ttt+1ll*l*p));
}
}
}
inline void bui(const int k,const int l,const int r)
{
tr[k].resize(r-l+3); sz[k]=r-l+1;
for(int i=1;i<=r-l+2;i++) tr[k][i]=inf; tr[k][0]=-inf;
if(l==r)
{
sum[k]=a[l]; tr[k][1]=p-a[l];
return;
}
const int mid=l+r>>1;
bui(mid<<1,l,mid); bui(mid<<1|1,mid+1,r);
pushup(k,mid);
}
inline LL que(const int k,const int l,const int r,const int L,const int R,LL v)
{
if(l>=L&&r<=R)
{
int x=upper_bound(tr[k].begin(),tr[k].end(),v)-tr[k].begin()-1;
return v+sum[k]-p*1ll*x;
}
const int mid=l+r>>1;
if(L<=mid) v=que(mid<<1,l,mid,L,R,v);
if(R>mid) v=que(mid<<1|1,mid+1,r,L,R,v);
return v;
}
} using namespace SEG;
char buf[1<<20],*p1,*p2;
#define gc() (p1 == p2 ? (p2 = buf + fread(p1 = buf, 1, 1 << 20, stdin), p1 == p2 ? EOF : *p1++) : *p1++)
#define read() ({\
int x = 0, f = 1;\
char c = gc();\
while(c < '0' || c > '9') f = (c == '-') ? -1 : 1, c = gc();\
while(c >= '0' && c <= '9') x = (x<<1) + (x<<3) + (c & 15), c = gc();\
f * x;\
})
inline void write(LL x)
{
x?(write(x/10),putchar((x%10)|48)):(0);
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
n=read(); m=read(); p=read();
for(int i=1;i<=n;i++) a[i]=read();
bui(1,1,n); LL ans=0;
while(m--)
{
int l=read()^ans,r=read()^ans,x=read()^ans; ans=que(1,1,n,l,r,x);
ans<0?(putchar('-'),write(-ans)):(ans?(write(ans)):(putchar('0'),void(0)));
putchar('\n'); ans=(ans%n+n)%n;
}
return 0;
}
CF494D
拆贡献直接做。分讨 \(u\) 在 \(v\) 的子树内和字数外的情况。
考验选手拆式子能力。
然后做完了。
code
#include<bits/stdc++.h>
using namespace std;
#define A(x) ((x%mod+mod)%mod)
#define mi(x,y) (dfn[x]<dfn[y]?(x):(y))
#define LL long long
const int N = 1e5+5,mod = 1e9+7;
int n,m;
int head[N],tot,dfn[N],num,st[30][N],lg[N];
struct E {int u,v; LL w;} e[N<<1];
inline void add(int u,int v,LL w) {e[++tot]={head[u],v,w}; head[u]=tot;}
LL d[N],d2[N],s[N],s2[N],g[N],sz[N],f[N];
void dfs(int u,int fa)
{
s[u]=d[u]; s2[u]=d2[u]; dfn[u]=++num; st[0][num]=fa; sz[u]=1;
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v; if(v==fa) continue;
d[v]=A(d[u]+e[i].w); d2[v]=A(d[v]*d[v]);
dfs(v,u); s[u]=A(s[u]+s[v]); s2[u]=A(s2[u]+s2[v]); sz[u]=A(sz[u]+sz[v]);
}
}
void dfs1(int u,int fa)
{
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v; if(v==fa) continue;
f[v]=A(f[u]-A(sz[v]*e[i].w)+A((n-sz[v])*e[i].w));
LL tmp=A(s2[v]+A(A(2*e[i].w)*s[v])+A(sz[v]*e[i].w%mod*e[i].w));
tmp=A(g[u]-tmp);
g[v]=A(tmp+A(A(2*e[i].w)*A(f[u]-s[v]-A(sz[v]*e[i].w)))+A((n-sz[v])*e[i].w%mod*e[i].w)+s2[v]);
dfs1(v,u);
}
}
inline int get(int x,int y)
{
if(x==y) return x;
if((x=dfn[x])>(y=dfn[y])) swap(x,y); x++;
int k=lg[y-x+1];
return mi(st[k][x],st[k][y-(1<<k)+1]);
}
inline LL dis(int x,int y)
{
return A(d[x]+d[y]-(d[get(x,y)]<<1));
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&n); lg[0]=-1;
for(int i=1;i<=n;i++) lg[i]=lg[i>>1]+1;
for(int i=1;i<n;i++)
{
int x,y; LL z; scanf("%d%d%lld",&x,&y,&z);
add(x,y,z); add(y,x,z);
}
dfs(1,0);
for(int i=1;i<=n;i++) s2[i]=A(s2[i]-A(A(2*d[i])*s[i])+A(A(sz[i]*d[i])*d[i])),s[i]=A(s[i]-A(sz[i]*d[i]));
for(int i=1;i<=20;i++)
for(int j=1;j<=n;j++)
st[i][j]=mi(st[i-1][j],st[i-1][j+(1<<(i-1))]);
g[0]=g[1]=s2[1]; f[0]=f[1]=s[1]; sz[0]=n;
dfs1(1,0);
scanf("%d",&m);
while(m--)
{
int x,y; scanf("%d%d",&x,&y);
int lca=get(x,y);
if(lca==y&&x!=y)
{
int k=st[0][dfn[y]]; LL ds=A(d[y]-d[k]);
LL tmp=A(s2[y]+A(2*A(ds*s[y]))+A(A(sz[y]*ds)*ds));
tmp=A(g[k]-tmp); ds=dis(x,k);
tmp=A(tmp+A(A(2*ds)*A(f[k]-s[y]-A(sz[y]*A(d[y]-d[k]))))+A((n-sz[y])*ds%mod*ds));
printf("%lld\n",A(g[x]-2*tmp));
}
else
{
LL ds=dis(x,y);
LL tmp=A(s2[y]+A(A(2*ds)*s[y])+A(sz[y]*ds%mod*ds));
printf("%lld\n",A(2*tmp-g[x]));
}
}
return 0;
}
墨墨的等式 跳楼机
问题是能通过 \(\sum a_ix_i\) 这个式子得到多少个值。
不妨讨论 \(ax+by+cz=ans\)。
因为值域较大,而单个值很小,我们从单独一个值入手,不如令 \(a \lt b \lt c\)。
然后考虑 \(by+cz\),显然有 \(by+cz \equiv ans \pmod{a}\),那么如果我们知道对于 \(by+cz\) \(\forall i \in [0,a)\),满足 \(by+cz \equiv i \pmod{a}\) 的最小值,就能直接知道个数。
然后最短路,连边为 \(u \to (u+b) \mod a\),\(u \to (u+c) \mod a\),设最短路为 \(d_i\),上界为 \(H\),那答案就是 \(\sum\lfloor \frac{H-d_i}{a} \rfloor + 1\),那个 \(+1\) 是不选 \(a\) 的情况。
Grand Test
发现一下,直接暴力推平复杂度是对的,因为如果一个点被染色两次,那么就已经找到一组解了。
具体而言建 dfs 树,然后对于每条返祖边,将两个端点间的路径染色。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
int n,m,T;
int head[N],tot;
struct E {int u,v;} e[N<<1];
inline void add(int u,int v) {e[++tot]={head[u],v}; head[u]=tot;}
int a[N],b[N],fa[N],dep[N];
bool vs[N],ins[N],fl;
int lca(int x,int y)
{
while(dep[x]>dep[y]) x=fa[x];
while(dep[y]>dep[x]) y=fa[y];
while(x!=y) x=fa[x],y=fa[y];
return x;
}
int st[N],top;
inline void getpath(int x,int y)
{
bool flf=0; int tmp=top;
if(dep[x]<dep[y]) flf=1,swap(x,y);
while(x!=y) st[++top]=x,x=fa[x];
st[++top]=y;
if(flf) reverse(st+tmp+1,st+1+top);
}
void get(int a,int b,int c,int d)
{
if(dep[b]>dep[d]) swap(a,c),swap(b,d);
int l=lca(a,c); top=0;
printf("%d %d\n",d,l);
getpath(d,l);
printf("%d ",top);
for(int i=1;i<=top;i++) printf("%d ",st[i]); putchar('\n'); top=0;
getpath(d,b); getpath(a,l);
printf("%d ",top);
for(int i=1;i<=top;i++) printf("%d ",st[i]); putchar('\n'); top=0;
st[++top]=d; getpath(c,l);
printf("%d ",top);
for(int i=1;i<=top;i++) printf("%d ",st[i]); putchar('\n'); top=0;
}
void dfs(int u)
{
if(fl) return;
vs[u]=ins[u]=1;
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v; if(v==fa[u]) continue;
if(!vs[v])
{
fa[v]=u; dep[v]=dep[u]+1;
dfs(v); if(fl) {ins[u]=0; return;}
}
else if(ins[v])
{
for(int x=u;x!=v;x=fa[x])
{
if(a[x]&&b[x])
{
get(a[x],b[x],u,v); fl=1; ins[u]=0;
return;
}
else
{
a[x]=u; b[x]=v;
}
}
}
}
ins[u]=0;
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&T);
while(T--)
{
fl=0;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int x,y; scanf("%d%d",&x,&y);
add(x,y); add(y,x);
}
for(int i=1;i<=n;i++) if(!vs[i]) dfs(i);
if(!fl) printf("-1\n");
for(int i=1;i<=n;i++) vs[i]=ins[i]=0,fa[i]=dep[i]=a[i]=b[i]=head[i]=0; tot=top=0;
}
return 0;
}
归程
咕了好久。。。
Kruskal 重构树。感觉理解还是不够深。
发现能否到达只和路径上的最小值有关。
而 Kruskal 重构树就是将两点间简单路径的最小值放进一个堆里。
一个节点子树内所有节点一定不小于它。两点 lca 的权值就是路径上最小值。
对于本题来说,先处理所有最短路,然后建重构树,能到达的点一定在一棵子树内,倍增处理即可。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+5,M = 4e5+5;
int n,m,T;
int head[N],tot,top,fa[N<<1],num,va[N<<1],son[N<<1][2],s[N<<1],f[30][N<<1];
struct E {int u,v,w,a;} e[M<<1],ed[M];
inline void add(int u,int v,int w) {e[++tot]={head[u],v,w}; head[u]=tot;}
inline int find(int x) {return x==fa[x]?(x):(fa[x]=find(fa[x]));}
void init()
{
memset(va,0,sizeof(va)); memset(son,0,sizeof(son)); memset(s,0x3f,sizeof(s));
memset(f,0,sizeof(f));
memset(head,0,sizeof(head)); tot=top=num=0;
}
namespace DJ
{
int d[N<<1]; bool vs[N];
void dj()
{
memset(d,0x3f,sizeof(d));
memset(vs,0,sizeof(vs));
priority_queue<pair<int,int>> q;
d[1]=0; q.push({0,1});
while(!q.empty())
{
int u=q.top().second; q.pop();
if(vs[u]) continue;vs[u]=1;
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v;
if(!vs[v]&&d[v]>d[u]+e[i].w)
{
d[v]=e[i].w+d[u];
q.push({-d[v],v});
}
}
}
}
} using namespace DJ;
void dfs(int u,int fa)
{
if(!u) return;
s[u]=d[u]; f[0][u]=fa;
for(int i=1;i<=20;i++) f[i][u]=f[i-1][f[i-1][u]];
dfs(son[u][0],u); dfs(son[u][1],u);
s[u]=min(s[u],min(s[son[u][0]],s[son[u][1]]));
}
inline int que(int x,int y)
{
for(int i=20;i>=0;i--) if(f[i][x]&&va[f[i][x]]>y) x=f[i][x];
return s[x];
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&T);
while(T--)
{
init();
scanf("%d%d",&n,&m);
for(int i=1;i<=n*2;i++) fa[i]=i;
for(int i=1;i<=m;i++)
{
int x,y,w,z; scanf("%d%d%d%d",&x,&y,&z,&w);
add(x,y,z); add(y,x,z); ed[i]={x,y,z,w};
}
dj();
sort(ed+1,ed+1+m,[&](const E &x,const E &y){return x.a>y.a;});
num=n;
for(int i=1;i<=m;i++)
{
int x=find(ed[i].u),y=find(ed[i].v);
if(x==y) continue;
fa[x]=fa[y]=++num; va[num]=ed[i].a;
son[num][0]=x; son[num][1]=y;
}
dfs(num,0);
int K,Q,S,ans=0;
scanf("%d%d%d",&Q,&K,&S);
while(Q--)
{
int x,y; scanf("%d%d",&x,&y); x=(x+K*ans-1)%n+1; y=(y+K*ans)%(S+1);
printf("%d\n",ans=que(x,y));
}
}
return 0;
}
TEST_68
树上 Trie。
咕了好久。。。
发现如果找到全局最大的两个点,除了他们的祖先,其他的点答案都一样。
Trie 维护全局的和两个点的祖先的就好了。
注意加入链上一个点的时候要把它除了目标路径上,其他的子树也加进去。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 5e5+5;
int n;
int head[N],tot;
struct E {int u,v;} e[N<<1];
inline void add(int u,int v) {e[++tot]={head[u],v}; head[u]=tot;}
int fa[N];
LL a[N],ans[N];
namespace Trie
{
int son[N*60][2],rt[3],num,p[N*60];
inline void clear() {for(int i=1;i<=num;i++) son[i][0]=son[i][1]=p[i]=0; num=0;}
inline void ins(int &k,LL x,int pos)
{
if(!k) k=++num; int now=k;
for(int i=60;i>=0;i--)
{
int c=x>>i&1;
if(!son[now][c]) son[now][c]=++num;
now=son[now][c];
}
p[now]=pos;
}
inline pair<LL,int> que(int k,LL x)
{
int now=k; LL res=0;
for(int i=60;i>=0;i--)
{
int c=x>>i&1;
if(son[now][c^1]) now=son[now][c^1],res+=1ll<<i;
else now=son[now][c];
}
return make_pair(res,p[now]);
}
} using namespace Trie;
int st[N],top;
bool vs[N];
LL dfs(int u,int k)
{
LL res=0; if(u!=1) res=que(rt[k],a[u]).first; ins(rt[k],a[u],u);
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v; if(vs[v]) continue;
res=max(dfs(v,k),res);
}
return res;
}
inline void cal(int k,int s)
{
top=0;
for(int i=1;i<=n;i++) vs[i]=0;
while(s) st[++top]=s,vs[s]=1,s=fa[s];
LL tmp=dfs(1,k);
for(int i=top;i>=1;i--)
{
int x=st[i];
if(x==1) {ans[x]=0; continue;}
ans[x]=tmp;
tmp=max(tmp,que(rt[k],a[x]).first); tmp=max(dfs(x,k),tmp);
}
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&n);
for(int i=2;i<=n;i++) scanf("%d",&fa[i]),add(fa[i],i);
int x=0,y=0; LL va=0;
for(int i=1;i<=n;i++)
{
ans[i]=-1;
scanf("%lld",&a[i]);
if(i==1) {ins(rt[0],a[i],i); continue;}
auto p=que(rt[0],a[i]);
if(p.first>va) va=p.first,x=i,y=p.second;
ins(rt[0],a[i],i);
}
clear(); cal(1,x); if(!vs[y]) clear(),cal(2,y);
for(int i=1;i<=n;i++) printf("%lld\n",ans[i]==-1?va:ans[i]);
return 0;
}
DZY Loves Chinese II
trick 线性基。
去掉一些边后判图连通性的做法:
跑出一棵 dfn 树,对于返祖边随机一个值,并将它覆盖的所有树边异或上这个值,询问时对于删的边插入线性基中判断是否有一条路径,树边和返祖边都被删。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5,M = 5e5+5;
int n,m,q;
int head[N],tot;
struct E {int u,v,id;} e[M<<1];
inline void add(int u,int v,int id) {e[++tot]={head[u],v,id}; head[u]=tot;}
mt19937 rd(time(0));
unsigned int va[M],d[N];
int dfn[N],num;
bool vs[N];
void dfs(int u,int f)
{
dfn[u]=++num;
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v;
if(dfn[v]>dfn[u]) va[e[i].id]=rd(),d[v]^=va[e[i].id],d[u]^=va[e[i].id];
else if(!dfn[v])dfs(v,u);
}
}
int dfs1(int u)
{
int res=d[u]; vs[u]=1;
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v; if(dfn[v]<dfn[u]||vs[v]) continue;
va[e[i].id]=dfs1(v); res^=va[e[i].id];
}
return res;
}
unsigned int ck[40];
inline bool ins(unsigned int x)
{
for(int i=31;i>=0;i--) if(x>>i&1)
{
if(!ck[i]) {ck[i]=x; return 1;}
x^=ck[i];
}
return 0;
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int x,y; scanf("%d%d",&x,&y);
add(x,y,i); add(y,x,i);
}
dfs(1,0); dfs1(1);
int ans=0;
scanf("%d",&q);
while(q--)
{
memset(ck,0,sizeof(ck));
int k,x; scanf("%d",&k);
bool fl=0;
for(int i=1;i<=k;i++)
{
scanf("%d",&x); x^=ans;
if(!ins(va[x])) fl=1;
}
if(fl) printf("Disconnected\n");
else printf("Connected\n"),ans++;
}
return 0;
}
aw

树上 dp。
好多 trick。
首先应该想到对每一条边按顺序定向,那么我们可以单独考虑每一条边的贡献。
发现计算所有方案不太可做。那么用到第二个 trick,转化为某一局面出现的概率,因为已经转化为边的贡献,所以只需要考虑对于一条边的能提供贡献的概率。
后面直接粘题解了。
注意一开始的状态转移方程中的概率是转移前的概率。所以先更新答案再转移。
code
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define LL long long
const int N = 1e5+5,mod = 998244353,D = 499122177;
int n;
int head[N],tot;
struct E {int u,v;} e[N<<1];;
inline void add(int u,int v) {e[++tot]={head[u],v}; head[u]=tot;}
pair<int,int> ed[N];
LL a[N],sz[N],dep[N],f[N],g[N];
void dfs(int u,int fa)
{
dep[u]=dep[fa]+1; sz[u]=a[u];
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v; if(v==fa) continue;
dfs(v,u); sz[u]=(sz[u]+sz[v])%mod;
}
}
inline LL qpow(LL a,int b)
{
LL res=1;
while(b)
{
if(b&1) res=res*a%mod;
a=a*a%mod; b>>=1;
}
return res;
}
int main()
{
freopen("aw.in","r",stdin);
freopen("aw.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%lld",&a[i]),f[i]=a[i],g[i]=a[i]*a[i]%mod;
for(int i=1;i<n;i++)
{
int x,y; scanf("%d%d",&x,&y);
ed[i]=make_pair(x,y); add(x,y); add(y,x);
}
dfs(1,0);
LL ans=0;
for(int i=1;i<n;i++)
{
int u=ed[i].fi,v=ed[i].se;
if(dep[u]>dep[v]) swap(v,u);
LL cu=(sz[1]-sz[v]+mod)%mod,cv=sz[v];
ans=(ans+cu*cv%mod+(cu-cv)*f[u]%mod-g[u]+mod)%mod;
ans=(ans+cu*cv%mod+(cv-cu)*f[v]%mod-g[v]+mod)%mod;
g[u]=g[v]=D*(g[u]+g[v]+2*f[u]*f[v]%mod)%mod;
f[u]=f[v]=D*(f[u]+f[v])%mod;
}
ans=ans*D%mod;
printf("%lld\n",ans*qpow(2,n-1)%mod);
return 0;
}
AGC010D
博弈论。
考虑只要出现过一个 \(1\) 后操作二就没有用了。
所以不妨先考虑没有操作二的情况,显然只需要判奇偶就行了,
那么操作二的作用就是改变奇偶性,发现奇公因数也是没有用的,
于是关键就是存在公因数 \(2\) 的情况,也就是全是偶数。
trick,这时考虑 先手优势,先手总能通过操作使场上存在 \(\gt 1\) 个奇数,那么后手永远不可能通过操作二改变奇偶性。
所以如果 \(\sum a_i-1\) 是奇数,那么无论如何先手必胜。
否则如果场上有 \(\gt 1\) 个奇数,那么先手操作一次后变成了上述情况中的后手,那么先手必败。
最后如果场上只有一个奇数,那么显然需要进行这次操作,然后整体除二,一共只会有 \(O(log V)\) 次。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
int n,a[N];
inline bool check()
{
int sum=0,cnt=0;
for(int i=1;i<=n;i++) sum^=((a[i]-1)&1),cnt+=(a[i]&1);
if(sum) return 1;
if(cnt>1) return 0;
for(int i=1;i<=n;i++) if(a[i]&1)
{
if(a[i]==1) return 0;
a[i]--;
}
int d=a[1];
for(int i=2;i<=n;i++) d=__gcd(d,a[i]);
for(int i=1;i<=n;i++) a[i]/=d;
return check()^1;
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
printf("%s\n",check()?"First":"Second");
return 0;
}
AGC014D
博弈论。
自然一点,就好像五子棋中能冲四就冲四,这样至少能牵制对方。
本题中也有类似的性质,如果先手占叶子的父亲,如果同时有大于一个叶子,直接赢了。
否则后手必须选这个叶子,相当于在树上删掉了两个点。
那不如一直这样操作,最后如果还剩下一个根连两个叶子的情况,那么先手必赢。
还原一下就是存在一个根有两个大小为奇数的子树(偶数的全被削掉了)。
然后就做完了。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
int n;
int head[N],tot;
struct E {int u,v;} e[N<<1];
inline void add(int u,int v) {e[++tot]={head[u],v}; head[u]=tot;}
int sz[N];
void dfs(int u,int f)
{
sz[u]=1; int tmp=0;
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v; if(v==f) continue;
dfs(v,u); sz[u]+=sz[v]; tmp+=(sz[v]&1);
}
tmp+=((n-sz[u])&1);
if(tmp>=2) {printf("First\n"); exit(0);}
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&n);
if(n==1) return printf("First\n"),0;
for(int i=1;i<n;i++)
{
int x,y; scanf("%d%d",&x,&y);
add(x,y); add(y,x);
}
dfs(1,0);
printf("Second\n");
return 0;
}
AGC010E
博弈论。
trick 是图论建模!
容易观察到的性质是不互质的两个数的相对位置不会改变,
然后能得到若干的连通块,每次后手贪心的选最大,保证不改变块内的顺序就行。
所以就是先手钦定连通块的顺序,然后后手选就行了。
第一个误区就是不互质不具有传递性,所以块内实际是存在拓扑序有向图,方向由先手确定的相对位置决定。
块内顺序怎么定呢(⊙o⊙)?
你贪心的把较小元素放在前面,然后发现小样例都过不去。
考虑先手能改变块内方向,所以肯定是从最小的开始,然后重新定向就行了。
最后可能是一个小 trick(是我太菜了连这也不会)。
我们想在保证拓扑序的前提下尽量选大的,把队列改成优先队列就行了
code
// LUOGU_RID: 197403435
#include<bits/stdc++.h>
using namespace std;
const int N = 2005;
int n,a[N],du[N],p[N][N],ans[N],d[N],m;
int mp[N][N];
bool vs[N];
int head[N],tot;
struct E {int u,v;} e[N*N];
inline void add(int u,int v) {e[++tot]={head[u],v}; head[u]=tot;}
void dfs(int u)
{
vs[u]=1;
for(int v=1;v<=n;v++) if(!vs[v]&&mp[u][v])
{
add(u,v); du[v]++;dfs(v);
}
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
sort(a+1,a+1+n);
for(int i=1;i<=n;i++)
for(int j=i+1;j<=n;j++)
if(__gcd(a[i],a[j])!=1) mp[i][j]=mp[j][i]=1;
for(int i=1;i<=n;i++) if(!vs[i]) dfs(i);
priority_queue<int> q;
for(int i=1;i<=n;i++) if(!du[i]) q.push(i);
while(!q.empty())
{
int u=q.top(); q.pop();
printf("%d ",a[u]);
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v;
if(!--du[v]) q.push(v);
}
}
return 0;
}
高手过招
博弈论。
普及 trick:阶梯 Nim。
显然直接 SG 函数统计不同子游戏的就好了,问题是对于单独游戏的处理。
于是学习了阶梯 Nim。
有n个位置1...n,每个位置上有ai个石子。有两个人轮流操作。操作步骤是:挑选1...n中任一一个存在石子的位置i,将至少1个石子移动至i−1位置(也就是最后所有石子都堆在在0这个位置)。谁不能操作谁输。求先手必胜还是必败。
结论:SG 函数就是奇数位上的异或和。
证明:先不考虑偶数位,只移动奇数位,发现就相当于一个只有奇数位的 Nim 游戏,
然后考虑目前的败方是否能通过移动偶数位改变自己的命运。
显然是不能的,因为他每移动一次偶数位,对方都有办法通过相同的移动使奇数位还原为最初的状态。
考虑这道题如何转化为阶梯 Nim。
考虑一个很典的思路,一个石子跳过它右边连续的石子,可以转化为石子段整体右移一位。
那么转化为阶梯就是转移到下一个阶梯。
但是还会有石子段的合并,也就是连在一起了。
解决方法是简单的,把石子段和它后面第一个空位一起看成一个阶梯就好了。
注意阶梯是从 \(0\) 号开始。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 1e3+5;
int T,n,a[30];
bool vs[30];
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
int ans=0;
while(n--)
{
int res=0,cnt=0,k=0,b=20;
scanf("%d",&k);
for(int i=1,x;i<=k;i++) scanf("%d",&x),vs[x]=1;
for(int i=b,c=0;i>=0;i--)
{
if(vs[i]) c++;
else if(vs[i+1]) a[cnt++]=c,c=0;
else a[cnt++]=0;
} cnt--;
for(int i=1;i<=cnt;i+=2) res^=a[i];
ans^=res;
memset(vs,0,sizeof(vs));
memset(a,0,sizeof(a));
}
if(ans) printf("YES\n");
else printf("NO\n");
}
return 0;
}
AGC029D
发现先手必须走,也就是横坐标一直在增加。
后手可以选择向上走,模样例就能发现能到达的点是联通的,且每一列只和最下面的点有关。
如果一个点左面是可达的,那么就是它了。记录每一列最小值即可。
注意横纵坐标不要看反!!!
code
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+5;
int n,h,w;
struct A {int x,y;} a[N];
int mi[N];
vector<int> g[N];
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d%d",&w,&h,&n);
for(int i=1;i<=n;i++) scanf("%d%d",&a[i].x,&a[i].y),g[a[i].x].push_back(i);
for(int i=1;i<=w;i++)
{
// printf()
mi[i]=mi[i-1]+1; mi[i]=min(h,mi[i]);
for(int j:g[i])
{
if(a[j].y<=mi[i-1]) {printf("%d\n",i-1); return 0;}
mi[i]=min(a[j].y-1,mi[i]);
}
}
printf("%d\n",w);
return 0;
}
AGC016F
博弈论,状压 dp。
显然用总方案数减去 \(SG(1)=SG(2)\) 的方案数比原问题容易的多。
考虑计算 \(SG(1)=SG(2)\) 的方案数。
可能是一个 trick,根据 \(SG(x)\) 的值给点分层。
根据 SG 函数就是 mex,那么显然有 SG 大的层中的点必须向每一个小的层连一条边,而 SG 小的层向大的层任意连边。
看到数据范围想到状压,于是我们可以维护点向集合连边的方案数(递推求目标集合中能连边的点的个数就行)。
然后枚举 \(SG(x) \ge x\) 的集合,再枚举 \(SG(x) = x\) 的集合,按上述方案连边。(注意要满足 1、2 在同一层中)
code
#include<bits/stdc++.h>
using namespace std;
const int N = 15,M = 125,mod = 1e9+7;
int n,m,_2[M];
int mp[N][N],c[N][1<<N],f[1<<N];
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d",&n,&m);
_2[0]=1; for(int i=1;i<=m;i++) _2[i]=_2[i-1]*2ll%mod;
for(int i=1;i<=m;i++)
{
int x,y; scanf("%d%d",&x,&y);
x--; y--;
mp[x][y]=1;
}
for(int i=1;i<(1<<n);i++)
{
int k=0; while(!(i>>k&1)) k++;
for(int j=0;j<n;j++)
c[j][i]=c[j][i^1<<k]+mp[j][k];//点向集合连边方案数
}
f[0]=1;
for(int s=1;s<(1<<n);s++)//s 枚举当前全集
{
for(int k=s;k;k=(k-1)&s) if((k&1)+(k>>1&1)!=1)//k 枚举当前的状态,1 2 在同一层即可
{
int t=s^k,C=1;
for(int i=0;i<n;i++)
{
if(t>>i&1) C=1ll*C*(_2[c[i][k]]-1)%mod;//大的向小的必须连,所以减去空集
if(k>>i&1) C=1ll*C*_2[c[i][t]]%mod;//小的向大的任意连
}
f[s]=(f[s]+1ll*f[t]*C)%mod;
}
}
printf("%lld\n",(1ll*_2[m]-f[(1<<n)-1]+mod)%mod);
return 0;
}
小约翰的游戏
学习了反Nim
其实就是记了结论,
先判断全是 \(1\) 的情况,剩下直接判断异或和。
证明:
-
全是 \(1\) 显然。
-
只有一个 \(\gt 1\) 的数,先手能使其变成情况 1,并且能决定奇偶,显然必胜,此时异或和一定不为 \(0\)。
-
有 \(\gt 1\) 个 \(\gt 1\) 的数,考虑异或和为零和不为零两种状态能且仅能相互转化,最终会变成情况 2,故异或和不为零先手必胜。
具体看 oi-wiki 吧。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 505;
int T;
int n,a[N],sum;
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&T);
while(T--)
{
scanf("%d",&n); int c=0; sum=0;
for(int i=1;i<=n;i++) scanf("%d",&a[i]),c+=(a[i]!=1),sum^=a[i];
if(!c) printf("%s\n",n&1?"Brother":"John");
else printf("%s\n",(!sum)?"Brother":"John");
}
return 0;
}
翻硬币
做到了小众 dp 题,没什么营养,但还是想不到。
也可能只是懒得想了?
注意到我们不在乎不同的位置,而只在乎有几个不同的。
设计状态 \(f_{i,j}\) 表示第 \(i\) 次操作时还有 \(j\) 个不同的(位置确定)。
转移时枚举当前操作了几个和目标不同的硬币,然后简单 dp。
还是太菜了。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 105,mod = 1e9+7;
int n,k,m,f[N][N],fac[N],inv[N],tot;
char s[N],t[N];
inline int C(int x,int y) {return x<y?0:1ll*fac[x]*inv[x-y]%mod*inv[y]%mod;}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d%d",&n,&k,&m);
scanf("%s%s",s+1,t+1);
for(int i=1;i<=n;i++) tot+=s[i]!=t[i];
fac[0]=fac[1]=inv[0]=inv[1]=1;
for(int i=2;i<=n;i++) fac[i]=1ll*fac[i-1]*i%mod,inv[i]=1ll*(mod-mod/i)*inv[mod%i]%mod;
for(int i=2;i<=n;i++) inv[i]=1ll*inv[i-1]*inv[i]%mod;
f[0][tot]=1;
for(int i=1;i<=k;i++)
{
for(int j=0;j<=n;j++)
{
for(int h=0;h<=min(m,j);h++)
{
int tmp=j+m-2*h;
if(tmp<0||tmp>n) continue;
f[i][tmp]=(f[i][tmp]+1ll*f[i-1][j]*C(j,h)%mod*C(n-j,m-h)%mod)%mod;
}
}
}
printf("%d\n",f[k][0]);
return 0;
}
黑白棋
学习 k-Nim,\(n\) 堆石子,轮流拿,每次选 \(k\) 堆任意拿(不为 \(0\)),谁不能操作谁输。
结论:如果对于每个二进制位 \(\sum_{i=1}^{n} [a_{i,j}=1] \pmod{k+1} =0\)(\(a_{i,j}\) 表示 \(a_{i}\) 在二进制下第 \(j\) 位),那么后手必胜。
证明是不是直接类比 Nim 和 Bash 的结合就好了?
本题容易抽象成 \(\frac{k}{2}\) 堆石子两人轮流拿的问题,然后单步容斥一下就是求后手必胜的方案,也就是每一位 \(1\) 的个数都要是 \(d+1\) 的倍数。
那么设计 \(f_{i,j}\) 表示考虑第 \(0 \sim i-1\) 位都满足条件且用了 \(j\) 个石子。
那么直接刷表 \(f_{i+1,j+x \times (d+1) \times 2^i} \gets f_{i,j} \times \binom{\frac{k}{2}}{x \times (d+1)}\)
表示这一位放 \(x \times (d+1)\) 个一,放在 \(\frac{k}{2}\) 堆里的方案数。
最后答案就是 \(\binom{n}{k} - \sum f_{\log_2n,i} \times \binom{n-i-\frac{k}{2}}{\frac{k}{2}}\)。
后面那个系数就是插板法。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 1e4+5,mod = 1e9+7;
int f[20][N],n,k,d;
int fac[N],inv[N];
inline long long C(int x,int y) {return x<y?0ll:1ll*fac[x]*inv[y]%mod*inv[x-y]%mod;}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d%d",&n,&k,&d);
fac[0]=fac[1]=inv[0]=inv[1]=1;
for(int i=2;i<=n;i++) fac[i]=1ll*fac[i-1]*i%mod,inv[i]=1ll*(mod-mod/i)*inv[mod%i]%mod;
for(int i=2;i<=n;i++) inv[i]=1ll*inv[i-1]*inv[i]%mod;
f[0][0]=1;
for(int i=0;i<=15;i++)
{
for(int j=0;j<=n-k;j++)
{
for(int x=0;j+x*(d+1)*(1<<i)<=n-k&&x*(d+1)<=k>>1;x++)
{
f[i+1][j+x*(d+1)*(1<<i)]=(f[i+1][j+x*(d+1)*(1<<i)]+f[i][j]*C(k>>1,x*(d+1))%mod)%mod;
}
}
}
int ans=0;
for(int i=0;i<=n-k;i++) ans=(ans+1ll*f[16][i]*C(n-i-(k>>1),k>>1)%mod)%mod;
printf("%lld\n",(C(n,k)-ans+mod)%mod);
return 0;
}
威佐夫博弈
博弈论。
令 \(m \lt n\),后手必胜,当且仅当 \(m = \lfloor (n-m) \times \frac{\sqrt{5}+1}{2} \rfloor\)。
原来世界这么奇妙。
code
#include<bits/stdc++.h>
using namespace std;
const long double del = (sqrtl(5.0)+1.0)/2.0;
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
int a,b; scanf("%d%d",&a,&b);
if(a<b) swap(a,b);
int tmp=a-b;
if(b==int(del*(long double)tmp)) printf("0");
else printf("1");
return 0;
}
awa

学习 border 树。
又顺便学了 AC自动机(因为博客还在咕咕咕,所以放了 oi-wiki 的链接)。
对于本题,容易想到枚举分割点,然后考虑用前缀和后缀拼接的方案数,然后赛时 SA 大战三个小时,发现无法去重!!!
由于要求的是二元组 \((x,y)\) 的个数,所以统计答案只能枚举前缀长度然后找不同的匹配后缀。
这个可以想到 KMP 统计匹配个数,再顺便想一下 border 树统计方案。
具体而言,border 树中的一个节点 \(x\) 表示了一个前缀 \(i\),它的父亲就是它的 \(border\),那么这一条根链上的点都是以 \(i\) 结尾的 border。
而子树内,就是这个前缀的所有出现位置。trick
然后就很妙啊!
我们分别对前缀和后缀建一棵 border 树(简称前缀、后缀树),对于前缀树的叶子节点,答案就是后缀树上能匹配的点到根的链,
对于剩下的点,答案就是子树内答案的并,考虑在线段树上维护,然后合并。
每次加一条链是不现实的,但考虑我们的操作,实际上就是建了一棵虚树,有结论:将虚树上的点按 dfs 序,虚树的大小就是 \(\sum dep_i+dep_{i-1}-dep_{lca(i,i-1)}\)。
显然线段树很好维护(我竟然调了这么久!!!)。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 4e5+5;
int n,m,T,n1,n2,fa1[N],fa2[N],rk[N];
char s[N],t[N],s1[N],s2[N];
int head[N],tot,rt[N];
struct E {int u,v;} e[N<<1];
inline void add(int u,int v) {e[++tot]={head[u],v}; head[u]=tot;}
vector<int> g[N];
namespace LCA
{
int dfn[N],num,st[30][N],d[N],lg[N];
void dfs(int u)
{
dfn[u]=++num; rk[num]=u; st[0][num]=fa2[u]; if(u) d[u]=d[fa2[u]]+1;
for(int v:g[u]) /*printf("%d %d$$$\n",u,v),*/dfs(v);
}
#define mi(x,y) (dfn[x]<dfn[y]?x:y)
inline void init(){for(int i=1;i<=20;i++) for(int j=1;j+(1<<i)-1<=n2+1;j++) st[i][j]=mi(st[i-1][j],st[i-1][j+(1<<(i-1))]); lg[0]=-1; for(int i=1;i<=n2;i++) lg[i]=lg[i>>1]+1;}
inline int get(int x,int y) {if(x==y) return x; if((x=dfn[x])>(y=dfn[y])) swap(x,y); x++; int k=lg[y-x+1]; return mi(st[k][x],st[k][y-(1<<k)+1]);}
} using namespace LCA;
namespace SEG
{
int num;
struct T {int l,r,ld,rd,sum;} tr[N<<5];
inline void pushup(int k)
{
int l=tr[k].l,r=tr[k].r;
if(!tr[k].l&&!tr[k].r) return ;
if(!tr[k].l) return tr[k]=tr[tr[k].r],tr[k].l=l,tr[k].r=r,void(0);
if(!tr[k].r) return tr[k]=tr[tr[k].l],tr[k].l=l,tr[k].r=r,void(0);
tr[k].ld=tr[tr[k].l].ld,tr[k].rd=tr[tr[k].r].rd;
tr[k].sum=tr[tr[k].l].sum+tr[tr[k].r].sum-(d[get(tr[tr[k].l].rd,tr[tr[k].r].ld)]);
}
inline void mdf(int &k,int l,int r,int p)
{
if(p<=1) return;
if(!k) k=++num;
if(l==r) return tr[k].ld=tr[k].rd=rk[p],tr[k].sum=d[rk[p]],void(0);
int mid=l+r>>1;
if(p<=mid) mdf(tr[k].l,l,mid,p);
else mdf(tr[k].r,mid+1,r,p);
pushup(k);
}
inline int merge(int x,int y,int l=1,int r=n2+1)
{
if(!x||!y) return x|y;
if(l==r) return x;
int mid=l+r>>1;
tr[x].l=merge(tr[x].l,tr[y].l,l,mid);
tr[x].r=merge(tr[x].r,tr[y].r,mid+1,r);
pushup(x);
return x;
}
inline void init()
{
for(int i=0;i<=num;i++) tr[i]={0,0,0,0,0};
num=0;
memset(rt,0,sizeof(rt));
for(int i=n+2;i<=n1-1;i++)
if(fa2[n2-i+n+1]!=0) mdf(rt[i],1,n2+1,dfn[fa2[n2-i+n+1]]);
}
} using SEG::merge; using SEG::tr;
long long ans;
void work(int u)
{
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v;
work(v);
rt[u]=merge(rt[u],rt[v]);
}
if(u<=n&&u) ans+=tr[rt[u]].sum;
}
int main()
{
freopen("awa.in","r",stdin);
freopen("awa.out","w",stdout);
scanf("%d",&T);
while(T--)
{
n1=n2=0; ans=0; LCA::num=0;
memset(head,0,sizeof(head)); tot=0;
scanf("%s%s",s+1,t+1); n=strlen(s+1); m=strlen(t+1);
for(int i=1;i<=n;i++) s1[++n1]=s[i]; s1[++n1]='#'; for(int i=1;i<=m;i++) s1[++n1]=t[i]; s1[n1+1]=0;
reverse(s+1,s+1+n); reverse(t+1,t+1+m);
for(int i=1;i<=n;i++) s2[++n2]=s[i]; s2[++n2]='#'; for(int i=1;i<=m;i++) s2[++n2]=t[i]; s2[n2+1]=0;
for(int i=2,j=0;i<=n1;i++)
{
while(j&&s1[i]!=s1[j+1]) j=fa1[j];
fa1[i]=(j+=s1[i]==s1[j+1]); add(fa1[i],i);
}
add(0,1);
for(int i=2,j=0;i<=n2;i++)
{
while(j&&s2[i]!=s2[j+1]) j=fa2[j];
fa2[i]=(j+=s2[i]==s2[j+1]); g[fa2[i]].push_back(i);
}
g[0].push_back(1);
dfs(0); init(); SEG::init(); work(0);
printf("%lld\n",ans);
for(int i=0;i<=n1;i++) g[i].clear();
}
return 0;
}
树V图
dp,还是太困难了。
首先注意到每个关键点的管辖点都形成一个连通块,考虑直接对连通块 dp。
\(f_{u}\) 表示 \(u\) 是关键点且满足了 \(u\) 及 \(u\) 子树内的所有限制的方案数。
转移时对连通块整体进行转移(类似于对连通块建了一棵新树)。
关键在于连通块交界处的那两个点,它们限定了我们对关键点的选择,所以钦定 \(u\) 为 \(x\) 的关键点时,枚举子连通块 \(y\) 内的每一个点作为关键点的方案数,考虑交界处的两个点的限制,统一进行转移。
这样一看好像确实不是特别困难,别害怕。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 3e3+5,mod = 998244353;
int T,n,a[N],f[N],x[N],y[N],w[N],k;
bool vs[N];
int head[N],tot;
struct E {int u,v;} e[N<<1];
inline void add(int u,int v) {e[++tot]={head[u],v}; head[u]=tot;}
inline void init() {memset(head,0,sizeof(head)); tot=0; memset(vs,0,sizeof(vs));}
void cal(int u,int fa,int co,int d)
{
w[d]=(w[d]+f[u])%mod;
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v; if(v==fa||a[v]!=co) continue;
cal(v,u,co,d+1);
}
}
void dp(int u,int fa,int co,int d,int y)
{
f[u]=1ll*f[u]*(1ll*w[d]+w[d+(co<y?-1:1)])%mod;
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v; if(v==fa||a[v]!=co) continue;
dp(v,u,co,d+1,y);
}
}
void dfs(int u,int fa)
{
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v; if(v==fa) continue;
dfs(v,u);
if(a[v]!=a[u])
{
for(int i=0;i<=n;i++) w[i]=0;
cal(v,u,a[v],0);
dp(u,v,a[u],0,a[v]);
}
}
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&T);
while(T--)
{
bool fl=0;
init();
scanf("%d%d",&n,&k);
for(int i=1;i<n;i++)
{
scanf("%d%d",&x[i],&y[i]);
add(x[i],y[i]); add(y[i],x[i]);
}
for(int i=1;i<=n;i++) scanf("%d",&a[i]),vs[a[i]]=1;
for(int i=1;i<=k;i++) if(!vs[i]) {fl=1; break;} if(fl) {printf("0\n"); continue;}
int tmp=0; for(int i=1;i<n;i++) tmp+=(a[x[i]]!=a[y[i]]); if(tmp>=k) {printf("0\n"); continue;}
for(int i=1;i<=n;i++) f[i]=1;
dfs(1,0);
int ans=0;
for(int i=1;i<=n;i++) if(a[i]==a[1]) ans=(ans+f[i])%mod;
printf("%d\n",ans);
}
return 0;
}
矩阵
数据结构,链表,码力大挑战。
赛时平衡树假了,赛后补了平衡树的 \(O(nq\log{n})\) 的代码,还没暴力分高。
放这看个乐子
#include<bits/stdc++.h>
using namespace std;
const int N = 3001,mod2 = 1e9+7,M = N*N*2,mod1 =998244353;
int n,q,ans,mp[N][N],a[N][N],anss;
inline int qpow(int a,long long b,int mod)
{
int res=1;
while(b)
{
if(b&1) res=1ll*res*a%mod;
a=1ll*a*a%mod; b>>=1;
}
return res;
}
namespace FHQ
{
int rtl[N],rth[N],tot,son[M][2],va[M],sz[M],pr[M],tag1[M],tag2[M],t1[N<<1],t2[N<<1],t3[N<<1];
inline void add(int k,int t1,int t2)
{
if(t1) swap(son[k][0],son[k][1]),tag1[k]^=t1;
if(t2) va[k]=(va[k]+t2)%mod2,tag2[k]=(tag2[k]+t2)%mod2;
}
inline void pushup(int k) {sz[k]=sz[son[k][0]]+sz[son[k][1]]+1;}
inline void pushdown(int k)
{
if(tag1[k]||tag2[k]) add(son[k][0],tag1[k],tag2[k]),add(son[k][1],tag1[k],tag2[k]);
tag1[k]=tag2[k]=0;
}
inline int merge(int x,int y)
{
if(!x||!y) return x|y;
if(pr[x]<=pr[y]) return pushdown(x),son[x][1]=merge(son[x][1],y),pushup(x),x;
else return pushdown(y),son[y][0]=merge(x,son[y][0]),pushup(y),y;
}
inline void split(int rt,int k,int &x,int &y)
{
if(!rt) return x=y=0,void(0);
pushdown(rt);
if(sz[son[rt][0]]+1<=k) x=rt,split(son[x][1],k-sz[son[rt][0]]-1,son[x][1],y);
else y=rt,split(son[y][0],k,x,son[y][0]);
pushup(rt);
}
inline int nw(int v) {va[++tot]=v; tag1[tot]=tag2[tot]=0; sz[tot]=1; pr[tot]=rand(); return tot;}
inline void ins(int &rt,int v)
{
rt=merge(rt,nw(v));
}
inline void mdf(int x1,int y1,int x2,int y2,int d)
{
for(int i=x1;i<=x2;i++)
{
int x,y,z;
split(rth[i],y1-1,x,y); split(y,y2-y1+1,y,z);
add(y,0,d); rth[i]=merge(merge(x,y),z);
}
for(int i=y1;i<=y2;i++)
{
int x,y,z;
split(rtl[i],x1-1,x,y); split(y,x2-x1+1,y,z);
add(y,0,d); rtl[i]=merge(merge(x,y),z);
}
}
inline void trans(int x1,int y1,int x2,int y2)
{
for(int i=x1;i<=x2;i++)
{
split(rth[i],y1-1,t1[i],t2[i]); split(t2[i],y2-y1+1,t2[i],t3[i]);
add(t2[i],1,0);
}
for(int i=y1;i<=y2;i++)
{
split(rtl[i],x1-1,t1[i+n],t2[i+n]); split(t2[i+n],x2-x1+1,t2[i+n],t3[i+n]);
}
for(int i=x1;i<=x2;i++)
rth[i]=merge(merge(t1[i],t2[y2-i+x1+n]),t3[i]);
for(int i=y1;i<=y2;i++)
rtl[i]=merge(merge(t1[i+n],t2[i-y1+x1]),t3[i+n]);
}
void dfs(int u)
{
if(!u) return;
pushdown(u);
dfs(son[u][0]);
anss=1ll*anss*12345%mod2;
ans=(ans+1ll*anss*va[u])%mod2;
dfs(son[u][1]);
}
} using namespace FHQ;
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d",&n,&q);
for(int i=1;i<=n;i++) a[i][0]=1;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
a[i][j]=1ll*a[i][j-1]*(i+1)%mod1;
ins(rth[i],a[i][j]); ins(rtl[j],a[i][j]);
}
}
while(q--)
{
int c; scanf("%d",&c);
if(c==1)
{
int x1,y1,x2,y2; scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
trans(x1,y1,x2,y2);
}
else
{
int x1,y1,x2,y2,d; scanf("%d%d%d%d%d",&x1,&y1,&x2,&y2,&d);
mdf(x1,y1,x2,y2,d);
}
}
anss=1;
for(int i=1;i<=n;i++) dfs(rth[i]);
printf("%d\n",ans);
return 0;
}
然后改十字链表,看了好久题解没有看懂,直到看到用图论理解,豁然开朗。
注意链表本质上就是一张图,然后就看题解吧,记得点个赞。
加上注释250行的码,留个纪念
code
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define A(x,y) (x+=y,x>=mod?x-=mod:0)
#define T(x) (x>=4?x-4:x)
const int N = 3050,mod1 = 998244353,mod = 1e9+7;
int n,q,b[N][N],tot,id[N][N];
long long anss=1,ans;
struct Node
{
int v[4],a,b[4];
// inline Node () {}
} a[N*N],aa[N*N];
inline int find(int x,int y)
{
return a[x].v[0]==y?0:(a[x].v[1]==y?1:(a[x].v[2]==y?2:3));
// if(a[x].v[0]==y) return 0;
// if(a[x].v[1]==y) return 1;
// if(a[x].v[2]==y) return 2;
// return 3;
}
inline int find1(int x,int y)
{
return aa[x].v[0]==y?0:(aa[x].v[1]==y?1:(aa[x].v[2]==y?2:3));
// if(a[x].v[0]==y) return 0;
// if(a[x].v[1]==y) return 1;
// if(a[x].v[2]==y) return 2;
// return 3;
}
// inline void add(int x,int y,int t1) {a[x].v[t1]=y;}
inline void to(int &now,int &fa,int t=2)
{
// if(now==id[0][0]) fa=now,now=a[now].v[2];
// else if(now==id[n+1][0]) fa=now,now=a[now].v[3];
// else if(now==id[0][n+1]) fa=now,now=a[now].v[1];
// else if(now==id[n+1][n+1]) fa=now,now=a[now].v[0];
// else
// {
int pr=find(now,fa);
// printf("~~%d %d\n",fa,now);
// print
// printf("%d:: ",now); for(int i=0;i<4;i++) printf("%d ",a[now].v[i]); putchar('\n');
fa=now; now=a[now].v[(pr+t)&3];
// printf("~~~%d %d\n",fa,now);
// }
}
inline void write(int now) {printf("%d:: ",now); for(int i=0;i<4;i++) printf("%d ",a[now].v[i]); putchar('\n');}
// bool vs[N];
inline void rnd(int s,int t,int d)
{
int now=s,fa=a[now].v[(t+2)&3];
// printf("%d %d&&&&\n",now,t);
for(int j=0;j<=3;j++)
{
int i=find(now,fa),k,kk;
fa=a[now].v[(i+1)&3];
// write(now);
for(int j=1;j<=d;j++)
{
aa[now]=a[now];
k=(find(now,fa)+1)&3; aa[a[now].v[k]]=a[a[now].v[k]];
// printf("%d %d %d&&\n",now,fa,a[now].v[k]);
// write(now);
to(now,fa);
}
k=(find(now,fa)+1)&3; kk=a[now].v[k];
// int tmp=k;
aa[kk]=a[kk];
k=(find(kk,now)+3)&3; kk=a[kk].v[k];
aa[kk]=a[kk];
// printf("%d %d %d %d&&\n",now,fa,a[now].v[tmp],kk);
// putchar('\n');
}
}
inline pair<int,int> goo(int s,int x)
{
int fa=s,now=a[s].v[3];
for(int i=1;i<x;i++) to(now,fa);
return make_pair(find(now,fa),now);
}
inline void change(int x,int fa,int v)
{
int pr=(find(x,fa)+1)&3,prr=find(a[x].v[pr],x);
// for(int i=0;i<4;i++) printf("%d ",a[x].v[i]); putchar('\n');
// for(int i=0;i<4;i++) printf("%d ",a[a[x].v[t]].v[i]); putchar('\n');
// putchar('\n');
// printf("%d %d###\n",a[x].v[pr],a[a[x].v[pr]].v[prr]);
// printf("%d %d\n",t,pr);
A(a[x].b[pr],v); A(a[a[x].v[pr]].b[prr],mod-v);
}
inline void mdf(int s,int t,int d1,int d2,int v)
{
int now=s,fa=a[now].v[(t+2)&3],d;
for(int j=0;j<=3;j++)
{
int i=find(now,fa);
fa=a[now].v[(i+1)&3];
d=(j&1?d2:d1);
// fa=a[now].v[(i+3)&3];
for(int j=1;j<=d;j++)
{
change(now,fa,v);
// printf("%d %d %d$$ \n",now,fa,d);
to(now,fa);
}
change(now,fa,v);
// printf("%d %d %d$$ \n",now,fa,d);
// putchar('\n');
}
}
inline void sp(int x,int y,int fax,int fay,int dis)
{
int i=(find(x,fax)+1)&3,j=(find(y,fay)+1)&3;
int to=aa[x].v[i],tv=(1ll*a[y].b[j]+dis)%mod,pr=find(to,x);
a[y].b[j]=tv; a[to].b[pr]=(mod-tv)%mod;
// printf("$$$%d %d %d\n",x,to,y);
// A(a[y].b[j],dis); A(a[to].b[tmp],mod-dis);
a[y].v[j]=to; a[to].v[pr]=y;
}
inline void del(int &dis,int x,int fa,int cc,int fl)
{
int t=(find(x,fa)+1)&3;
int too=aa[x].v[t],pr=find1(too,x);
// printf("%d %d %d %d$$$\n",x,too,aa[too].v[(pr+cc)&3],fl);
A(dis,(1ll*aa[too].b[(pr+cc)&3]*fl+mod)%mod);
}
inline void trans(int s,int t,int x)
{
int l=s,r=s,dis=0,fal=a[s].v[(t+2)&3],far=fal;
int i=(t+2)&3,j=i;
far=a[r].v[(j+1)&3];
for(int k=1;k<=x;k++)
{
// printf("%d %d$$\n",r,far);
to(r,far);
del(dis,r,far,1,1);
// printf("%d %d\n",r,far);
}
// printf("%d %d$$\n",r,far);
del(dis,r,far,3,-1);
j=find(r,far); i=find(l,fal);
far=a[r].v[(j+1)&3]; fal=a[l].v[(i+1)&3];
// printf("%d %d^^^^^^^^^^^^\n",fal,far);
// printf("***%d %d\n",r,far);
// printf("%d:: ",r); for(int k=0;k<4;k++) printf("%d ",a[r].v[k]); putchar('\n');
del(dis,r,far,1,1);
for(int k=1;k<=(x+1)*4;k++)
{
// j=find(r,far)+1; i=find(l,fal)+1;
sp(r,l,far,fal,mod-dis);
// printf("%d:: ",l); for(int h=0;h<4;h++) printf("#%d#",a[l].v[h]); putchar('\n');
if(k%(x+1)==0)
{
// printf("***");
del(dis,l,fal,3,1); del(dis,r,far,3,-1);
i=find(l,fal); j=find(r,far);
far=a[r].v[(j+1)&3]; fal=a[l].v[(i+1)&3];
// del(dis,l,i,1,-1); del(dis,r,j,1,1);
}
else to(l,fal),to(r,far);
// printf("***");
del(dis,l,fal,1,-1); del(dis,r,far,1,1);
}
// putchar('\n');
// printf("%d\n",dis);
}
// inline void debug(int now,int fa,int d,int x)
// {
// // now<10?printf("%d ",now):printf("%d ",now);
// if(!now||now==id[x][n+1]) return;
// // anss=1ll*anss*12345%mod;
// // A(d,a[now].b[find(now,fa)]); A(a[now].a,d); A(ans,1ll*a[now].a*anss%mod);
// // printf("%d ",(a[now].a)%mod);
// to(now,fa,2); debug(now,fa,d,x);
// }
inline void que(int now,int fa,int d,int x)
{
if(!now||now==id[x][n+1]) return;
anss=1ll*anss*12345%mod;
A(d,a[now].b[find(now,fa)]); A(a[now].a,d); A(ans,1ll*a[now].a*anss%mod);
// printf("%d ",(a[now].a)%mod);
// now<=99?(now<10?printf("%d ",now):printf("%d ",now)):printf("%d ",now);
to(now,fa,2); que(now,fa,d,x);
}
inline int read()
{
int res=0; char x=getchar();
while(x<'0'||x>'9') x=getchar();
while(x<='9'&&x>='0') res=(res<<1)+(res<<3)+(x^48),x=getchar();
return res;
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d",&n,&q);
for(int i=0;i<=n+1;i++)
for(int j=0;j<=n+1;j++) id[i][j]=++tot;
for(int i=1;i<=n;i++) b[i][0]=1;
for(int i=0;i<=n+1;i++)
{
for(int j=0;j<=n+1;j++)
{
if(i>=1&&i<=n&&j>=1&&j<=n)b[i][j]=1ll*b[i][j-1]*(i+1)%mod1,
a[id[i][j]].a=b[i][j];
a[id[i][j]].v[0]=id[i-1][j];
a[id[i][j]].v[2]=id[i+1][j];
a[id[i][j]].v[1]=id[i][j-1];
a[id[i][j]].v[3]=id[i][j+1];
// add(id[i][j],id[i-1][j],0);
// add(id[i][j],id[i+1][j],2);
// add(id[i][j],id[i][j-1],1);
// add(id[i][j],id[i][j+1],3);
// printf("%d::",id[i][j]); for(int k=0;k<3;k++) printf("%d ",a[id[i][j]].v[k]); putchar('\n');
}
}
// for(int i=0;i<=n+1;i++)
// {
// for(int j=0;j<=n+1;j++)
// id[i][j]<=99?(id[i][j]<10?printf("%d ",id[i][j]):printf("%d ",id[i][j])):printf("%d ",id[i][j]);
// putchar('\n');
// }
while(q--)
{
// for(int i=0;i<=n+1;i++) id[i][0]<10?printf("%d ",id[i][0]):printf("%d ",id[i][0]),debug(a[id[i][0]].v[3],id[i][0],0,i),putchar('\n');
// putchar('\n');
int c=read();
if(c==1)
{
int x1=read(),y1=read(),x2=read(),y2=read();
if(x1==x2) continue;
// pair<int,int> tmp1;
// if(y1-1>=1) tmp1=goo(id[x1-1][0],y1-1); else tmp1=make_pair(1,id[x1-1][0]);
pair<int,int> tmp=goo(id[x1][0],y1);
// printf("%d %d %d %d\n",x1,y1,tmp1.fi,tmp1.se);
// rnd(tmp1.se,tmp1.fi,x2-x1+2);
rnd(tmp.se,tmp.fi,x2-x1); trans(tmp.se,tmp.fi,x2-x1);
}
else
{
int x1=read(),y1=read(),x2=read(),y2=read(),d=read();
pair<int,int> tmp=goo(id[x1][0],y1);
// printf("%d %d\n",tmp.fi,tmp.se);
// printf("%d %d\n",x2-x1,y2-y1);
mdf(tmp.se,tmp.fi,x2-x1,y2-y1,d);
}
}
for(int i=1;i<=n;i++) que(a[id[i][0]].v[3],id[i][0],0,i);
printf("%lld\n",ans);
// cerr<<1.0*clock()/CLOCKS_PER_SEC;
return 0;
}
拉丁方
学习二分图边染色!
板子是这个 CF600F。
一个二分图给边染色,使相邻的边不同色,问最少染多少种颜色。
方法是枚举每一条边,找端点染色的 \(mex\),如果相同直接染,如果不同考虑暴力协商。
不相同一定是有冲突,找到冲突的那条边,然后强行修改,再对这条边对面的那个进行暴力协商。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 2005,M = 1e5+5;
int a[N],b[N],x[M],y[M],n,m,e;
int du[N],ans;
int vs[N][N];
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d%d",&n,&m,&e);
for(int i=1;i<=e;i++)
{
scanf("%d%d",&x[i],&y[i]);
y[i]+=n; du[x[i]]++; du[y[i]]++;
ans=max(du[x[i]],ans); ans=max(du[y[i]],ans);
}
for(int i=1;i<=e;i++)
{
int co1=1,co2=1;
while(vs[x[i]][co1]) co1++;
while(vs[y[i]][co2]) co2++;
vs[x[i]][co1]=y[i];
vs[y[i]][co2]=x[i];
if(co1==co2) continue;
for(int tmp=co2,w=y[i];w;w=vs[w][tmp],tmp^=co1^co2)
swap(vs[w][co1],vs[w][co2]);
}
printf("%d\n",ans);
for(int i=1;i<=e;i++)
{
for(int j=1;j<=ans;j++) if(vs[x[i]][j]==y[i]) printf("%d ",j);
}
return 0;
}
对于本题,把行向能填的数字连边,然后将列的限制看成对边染色。
先考虑 \(R=n\) 的情况,那么只有右边,是好做的。
然后 \(R\ne n\),那么就是对右边做完再对左下角做一遍。
可以直接封成结构体。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 505;
struct P
{
int a,b,vs[N<<1][N];
inline void init(int x,int y)
{
a=x; b=y;
memset(vs,0,sizeof(vs));
}
inline void add(int u,int v)
{
v+=a;
int x=1,y=1;
while(vs[u][x]) x++; while(vs[v][y]) y++;
vs[u][x]=v; vs[v][y]=u;
if(x==y) return;
for(int w=v,tmp=y;w;w=vs[w][tmp],tmp^=x^y) swap(vs[w][x],vs[w][y]);
}
} g;
int d[N],a[N][N],n,R,C,T;
bool vs[N];
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&T);
while(T--)
{
bool fl=0;
scanf("%d%d%d",&n,&R,&C);
for(int i=1;i<=n;i++) d[i]=R;
for(int i=1;i<=R;i++) for(int j=1;j<=C;j++) scanf("%d",&a[i][j]),--d[a[i][j]];
for(int i=1;i<=n;i++) if(d[i]>n-C) {printf("No\n"); fl=1; break;};
if(fl) continue;
g.init(R,n);
for(int i=1;i<=R;i++)
{
memset(vs,0,sizeof(vs));
for(int j=1;j<=C;j++) vs[a[i][j]]=1;
for(int j=1;j<=n;j++) if(!vs[j]) g.add(i,j);
}
for(int i=1;i<=R;i++) for(int j=1;j<=n-C;j++) a[i][j+C]=g.vs[i][j]-R;
g.init(n,n);
for(int i=1;i<=n;i++)
{
memset(vs,0,sizeof(vs));
for(int j=1;j<=R;j++) vs[a[j][i]]=1;
for(int j=1;j<=n;j++) if(!vs[j]) g.add(i,j);
}
for(int i=1;i<=n;i++) for(int j=1;j<=n-R;j++) a[j+R][i]=g.vs[i][j]-n;
printf("Yes\n");
for(int i=1;i<=n;i++) {for(int j=1;j<=n;j++) printf("%d ",a[i][j]); putchar('\n');}
}
return 0;
}
一直在你身旁
接下来是好多 dp。
其实是能想到的。
\(O(n^3)\) 的区间 DP 很显然。\(f_{l,r}=max(f_{l,p-1}+a_{p-1},f_{p,r}+a_{p-1})_{p=l}^r\)。
优化观察性质,发现 \(a\) 是单调不降的,考虑单调队列优化。
\(f_{l,p-1}+a_{p-1}\) 显然是单调,用一个指针扫就能找到第一个不小于 \(f_{p,r}+a_{p-1}\) 的,也就是第一个有贡献的。
但是 \(f_{p,r}+a_{p-1}\) 好像没有什么性质。
假设一下,如果 \(f_{p,r}+a_{p-1}\) 是单调不增的,那么一个不增,一个不降,会有一个交点,我们又是要取最大值的最小,答案显然是交点左右的两个位置。
但是 \(f_{p,r}+a_{p-1}\) 没有上述性质,好像假了。
没有性质就创造性质,对 \(f_{p,r}+a_{p-1}\) 维护单调队列,那么队列里面的就是单调的,按上述方法做即可。
注意我们只在乎单调队列里的 \(f_{p,r}+a_{p-1}\),因为队列外的一定不优。并且队列里的点不一定是连续的,所以可能的决策点不一定是两个相邻的。
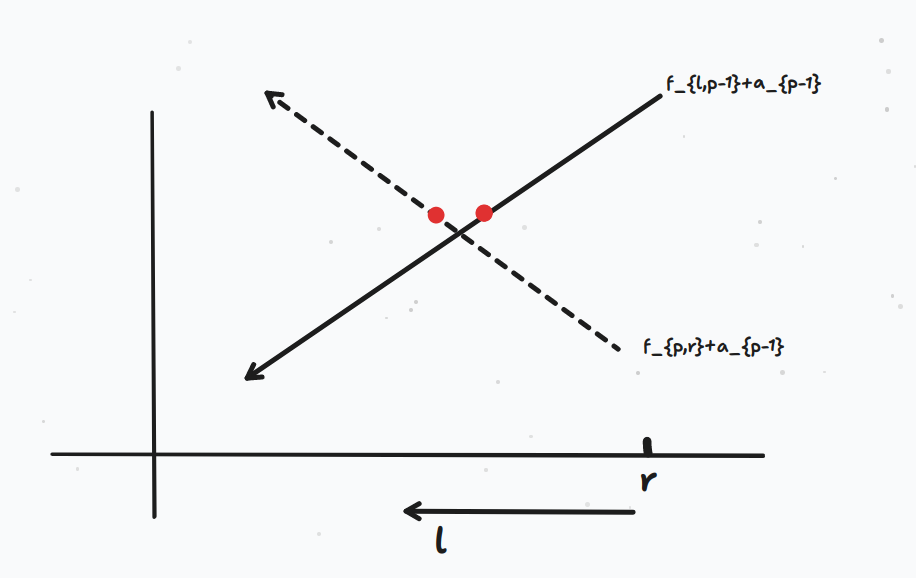
对于每一个 \(r\) 倒序枚举 \(l\),虚线是由于只有队列里的点。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const LL inf = 1e16;
const int N = 7101;
int T,n,a[N];
LL f[N][N];
int q[N<<1],L,R;
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int r=2;r<=n;r++)
{
L=1,R=1; q[1]=r-1; f[r-1][r]=a[r-1];
for(int l=r-2,p=r;l>=1;l--)
{
while(p>l&&f[l][p-1]>f[p][r]) p--;
f[l][r]=f[l][p]+a[p];
while(L<=R&&q[L]>=p) L++;
if(L<=R) f[l][r]=min(f[l][r],f[q[L]+1][r]+a[q[L]]);
while(L<=R&&f[q[R]+1][r]+a[q[R]]>=f[l+1][r]+a[l]) R--;
q[++R]=l;
}
}
printf("%lld\n",f[1][n]);
}
return 0;
}
Building Bridges
李超线段树维护斜率优化板子。
发现李超线段树出奇的好写。
李超线段树维护斜率优化比凸包维护斜率优化好想的多。
要求 \(f_i\),那么就令 \(f_i\) 作为 \(y_i\),令乘积项中的 \(f(i)\) 作为 \(x_i\),那么每一个 \(j\) 就唯一确定了一条直线,求 \(x_i\) 处 \(y_i\) 的最小值。
然后就是李超线段树。注意赋初值。李超线段树其实是一个类似标记永久化的东西,查询时别忘了记路径上的值。
凸包维护斜率优化是将要求的项放在截距的位置,每次插入一个点,查询一个斜率过哪个点截距最优,根据查询的 \(k\)、插入的 \(x\)、和 最大最小值判断凸包形状和单调栈还是单调队列。
单调栈和单调队列的区别其实就是插入点的方向和取答案(相切)的方向是否一样。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 1e5+5,M = 1e6;
int n;
LL h[N],w[N],a[N],b[N],f[N];
namespace LC
{
inline LL g(int x,int k) {return a[k]*x+b[k];}
int tr[(M+5)<<2];
inline void mdf(int k,int l,int r,int v)
{
if(l==r)
{
if(g(l,v)<g(l,tr[k])) tr[k]=v;
return;
}
int mid=l+r>>1;
if(g(mid,v)<g(mid,tr[k])) swap(v,tr[k]);
if(g(l,v)<g(l,tr[k])) mdf(k<<1,l,mid,v);
if(g(r,v)<g(r,tr[k])) mdf(k<<1|1,mid+1,r,v);
}
inline LL que(int k,int l,int r,int p)
{
if(l==r) return g(p,tr[k]);
int mid=l+r>>1; LL res=g(p,tr[k]);
if(p<=mid) return res=min(res,que(k<<1,l,mid,p));
else return res=min(que(k<<1|1,mid+1,r,p),res);
}
} using namespace LC;
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&n); b[0]=1e18;
for(int i=1;i<=n;i++) scanf("%lld",&h[i]);
for(int i=1;i<=n;i++) scanf("%lld",&w[i]),w[i]+=w[i-1];
a[1]=-2*h[1]; b[1]=h[1]*h[1]-w[1]; mdf(1,0,M,1);
for(int i=2;i<=n;i++)
{
f[i]=que(1,0,M,h[i])+h[i]*h[i]+w[i-1];
a[i]=-2*h[i]; b[i]=f[i]+h[i]*h[i]-w[i];
mdf(1,0,M,i);
}
printf("%lld\n",f[n]);
return 0;
}
AGC026D
想到第一点,想不到第二点。。。
能想到对于每一列考虑,只能和上一列全不同,或者如果上一列全是红蓝交叉的,那么可以完全相同。
想不到设计状态(好像这个更显?),\(f_{i,j}\) 表示第 \(i\) 列,最下面 \(j\) 个是红蓝交叉,上面的都不是的方案数。
当然需要离散化。注意这里离散化的是段,而不是点,所以最开始补一项 \(1\),并且后面也要注意。
转移分讨一下(为与代码一致,消去第一维):
-
\(h_i \le h_{i-1}:\ \ f_{h_i} \gets f_{h_i} \times 2 ,\ f_{h_i} \gets f_{h_i}+\sum_{j=h_i+1}^{h_{i-1}} f_{j} \times 2,\ f_{j} \gets 0\)
-
\(h_i \gt h_{i-1}:\ \ \forall{j \in [1,h_{i-1})},\ f_j \gets f_j \times 2^{h_{i}-h_{i-1}},\ \forall{j \in [h_{i-1},h_{i}]},\ f_{j} \gets 2 \times f_{h_{i-1}} \times (2^{h_i-c_j}-2^{h_i-c_{j+1}})\)
\(h_i\) 表示真实值,\(c_i\) 表示离散化后 \(i\) 对应的真实值(段)。
解释以下 \((2^{h_i-c_j}-2^{h_i-c_{j+1}})\),根据上文所说,离散化的是段,我们对于一个"点"求得其实是对应段的值。
所以应该是钦定 \(c_{j+1}\) 和前一个位置相同,求 \(\sum_{k=c_j+1}^{c_{j+1}} 2^{h_i-k-1}\),用差分或者积分一下,就变成 \((2^{h_i-c_j}-2^{h_i-c_{j+1}})\)。
奇妙笛卡尔数能做到 \(o(n\log n)\),但是不会。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 105,mod = 1e9+7;
int n,h[N],tl[N],tot;
unordered_map<int,int> mp;
LL f[N];
inline LL qpow(LL a,LL b)
{
if(b<0) return 0;
LL res=1;
while(b)
{
if(b&1) res=res*a%mod;
a=a*a%mod; b>>=1;
}
return res;
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&h[i]),tl[++tot]=h[i]; tl[++tot]=1;
sort(tl+1,tl+1+tot);
tot=unique(tl+1,tl+1+tot)-tl-1; tl[tot+1]=1e9;
for(int i=1;i<=tot;i++) mp[tl[i]]=i;
for(int i=1;i<=n;i++) h[i]=mp[h[i]];
for(int i=1;i<=h[1];i++) f[i]=2ll*(qpow(2,tl[h[1]]-tl[i])-qpow(2,tl[h[1]]-tl[i+1])+mod)%mod;
for(int i=2;i<=n;i++)
{
if(h[i]<h[i-1])
{
f[h[i]]=(f[h[i]]*2)%mod;
for(int j=h[i]+1;j<=h[i-1];j++) (f[h[i]]+=f[j]*2%mod)%=mod,f[j]=0;
}
else
{
LL v=f[h[i-1]];
for(int j=1;j<h[i-1];j++) f[j]=f[j]*qpow(2,tl[h[i]]-tl[h[i-1]])%mod;
for(int j=h[i-1];j<=h[i];j++)
f[j]=2ll*v%mod*(qpow(2,tl[h[i]]-tl[j])+mod-qpow(2,tl[h[i]]-tl[j+1]))%mod;//差分
}
}
LL ans=0;
for(int i=1;i<=h[n];i++) ans=(ans+f[i])%mod;
printf("%lld\n",ans);
return 0;
}
序列分割
乍一看不太可做。发现一下性质。
发现割的顺序和答案无关(好像是挺常见的性质,再多想一会可能能想到)。
然后直接 DP + 斜率优化。分层进行。
注意有一个唐氏写法。每次在预先把下一层的凸包建出来,错的很显然。
还有注意算斜率时斜率不存在的情况。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 1e5+5,M = 205;
int n,K;
LL a[N],f[2][N];
inline int read()
{
int res=0; char x=getchar();
while(x<'0'||x>'9') x=getchar();
while(x<='9'&&x>='0') res=(res<<1)+(res<<3)+(x^48),x=getchar();
return res;
}
#define x(c) (a[c])
#define y(c,d) (a[c]*a[n]-f[d][c])
inline long double kkk(int c,int d,int e)
{
if(x(d)==x(c)) return -1e18;//!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
return 1.00*(y(d,e)-y(c,e))/(x(d)-x(c));
}
#define b(c) (a[n]*a[i]-a[i]*a[i])
int q[2][N<<1],l[2],r[2],pre[N][M];
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
n=read(); K=read();
for(int i=1;i<=n;i++) a[i]=read(),a[i]+=a[i-1];
for(int k=1;k<=K;k++)
{
int j=k&1; l[j^1]=1; r[j^1]=0;
q[j^1][++r[j^1]]=0;
for(int i=1;i<=n;i++)
{
while(l[j^1]<r[j^1]&&kkk(q[j^1][l[j^1]+1],q[j^1][l[j^1]],j^1)<=a[i]) l[j^1]++;
f[j][i]=a[i]*x(q[j^1][l[j^1]])+b(i)-y(q[j^1][l[j^1]],j^1); pre[i][k]=q[j^1][l[j^1]];
while(l[j^1]<r[j^1]&&kkk(q[j^1][r[j^1]],q[j^1][r[j^1]-1],j^1)>=kkk(i,q[j^1][r[j^1]],j^1)) r[j^1]--;
q[j^1][++r[j^1]]=i;
}
}
LL ans=-1; int now=0;
for(int i=1;i<=n;i++) if(f[K&1][i]>ans) ans=f[K&1][i],now=i;
printf("%lld\n",ans);
for(int k=K;now&&k;now=pre[now][k],k--) printf("%d ",now);
return 0;
}
忘情
学习 WQS 二分,式子很容易推出 \(f_{i,k}=min(f_{j,k-1}+(s_i-s_j+1)^2)\)(好像是)。
直接斜率优化就是 \(O(nk)\) 的,然后加个 WQS 二分就是 \(O(n\log V)\) 的。
很套路。
code
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define LL long long
const int N = 1e5+5;
const LL K = 1e18;
int n,m;
LL s[N],f[N];
int q[N],l,r,pre[N];
#define y(k) (s[k]*s[k]-2*s[k]+f[k])
#define x(k) (2*s[k])
#define k(a,b) ((1.0*y(b)-y(a))/(x(b)-x(a)))
inline pair<int,LL> check(LL k)
{
l=1,r=1; q[1]=0;
for(int i=1;i<=n;i++) pre[i]=0;
for(int i=1;i<=n;i++)
{
while(l<r&&k(q[l],q[l+1])<s[i]) l++;
f[i]=f[q[l]]+(s[i]-s[q[l]]+1)*(s[i]-s[q[l]]+1)+k; pre[i]=q[l];
while(l<r&&k(q[r-1],q[r])>=k(i,q[r])) r--;
q[++r]=i;
}
int cnt=0,now=n;
while(pre[now]) cnt++,now=pre[now];
return make_pair(cnt,f[n]);
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%lld",&s[i]),s[i]=s[i-1]+s[i];
LL l=-K,r=K,res=0,k=0;
while(l<=r)
{
LL mid=l+r>>1;
auto tmp=check(mid);
if(tmp.fi<m) res=tmp.se,k=mid,r=mid-1;
else l=mid+1;
}
printf("%lld\n",res-k*m);
return 0;
}
CF1175G
斜率优化好题。
式子是 \(f_{i,k}=min(f_{j,k-1}+(i-j)\times \max_{j+1\leq k\leq i}\{a_k\})\),问题是怎么处理那个 \(max\),
直接做显然不行,我们考虑用单调栈将 \(max\) 转化成定值,然后对每个区间求解。
假设区间的 \(max\) 是定值,那么对于这个区间的答案显然是好求的,但是我们维护的是单调栈,会涉及区间的合并,所以对于这个区间来说 \(max\) 还可能变大,所以其实还是一个斜率优化的问题,每次需要合并两个凸包或者李超线段树。
这考虑的是对于一个小区间内的,对于整体,那就是好几个区间,每个区间的最有决策点都是可求的,所以在做一遍类似的斜率优化就行了。
我写的李超线段树,你发现区间合并后原来在大树上一些被覆盖的点可能会活,所以还需要维护李超线段树的撤销,开栈记修改时间、位置和值就行。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 2e4+5,M = 2e4;
const LL inf = LLONG_MAX;
int n,k,a[N];
LL f[N],g[N];
int st[N],top;
namespace LC
{
struct B {int t,p,x;} b[N<<5];
int tim,btop;
int rt[N],num,tot;
struct L
{
LL k,b;
inline LL K(int x) const {return k*x+b;}
} lin[N<<1];
struct T {int l,r,v;} tr[N<<5];
inline void clear()
{
memset(rt,0,sizeof(rt));
for(int i=0;i<=num;i++) tr[i].l=tr[i].r=tr[i].v=0;
tot=btop=num=top=0;
}
inline void mdf(int &k,int l,int r,int v,bool fl)
{
if(!k) return tr[k=++num].v=v,(fl?(b[++btop]={tim,k,0}):B()),void(0);
if(l==r) return lin[v].K(l)<lin[tr[k].v].K(l)?((fl?b[++btop]={tim,k,tr[k].v}:B()),tr[k].v=v):0,void(0);
int mid=l+r>>1;
lin[v].K(mid)<lin[tr[k].v].K(mid)?((fl?b[++btop]={tim,k,tr[k].v}:B()),swap(tr[k].v,v)):void(0);
if(lin[v].K(l)<lin[tr[k].v].K(l)) mdf(tr[k].l,l,mid,v,fl);
if(lin[v].K(r)<lin[tr[k].v].K(r)) mdf(tr[k].r,mid+1,r,v,fl);
}
inline int merge(int x,int y,int l,int r)
{
if(!x||!y) return x|y;
if(l==r) return tr[x].v=lin[tr[y].v].K(l)<lin[tr[x].v].K(l)?tr[y].v:tr[x].v,x;
int mid=l+r>>1;
lin[tr[y].v].K(mid)<lin[tr[x].v].K(mid)?swap(tr[x].v,tr[y].v):void(0);
tr[x].l=merge(tr[x].l,tr[y].l,l,mid); tr[x].r=merge(tr[x].r,tr[y].r,mid+1,r);
mdf(x,l,r,tr[y].v,0);
return x;
}
inline LL que(int k,int l,int r,int p)
{
if(!k) return inf;
if(l==r) return lin[tr[k].v].K(p);
int mid=l+r>>1;
return min(lin[tr[k].v].K(p),p<=mid?que(tr[k].l,l,mid,p):que(tr[k].r,mid+1,r,p));
}
} using namespace LC;
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d",&n,&k); lin[0]={0,inf};
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
memset(g,0x3f,sizeof(g)); g[0]=0;
for(int i=1;i<=k;i++)
{
clear();
for(int j=1;j<=n;j++)
{
lin[++tot]={-(j-1),g[j-1]}; mdf(rt[j],1,M,tot,0);
while(top&&a[st[top]]<a[j])
{
while(btop&&b[btop].t==st[top])
tr[b[btop].p].v=b[btop].x,btop--;
rt[j]=merge(rt[j],rt[st[top]],1,M);
top--;
}
lin[++tot]={a[j],que(rt[j],1,M,a[j])}; tim=st[++top]=j; mdf(rt[0],1,n,tot,1);
f[j]=que(rt[0],1,n,j);
}
for(int j=1;j<=n;j++) g[j]=f[j];
}
printf("%lld\n",f[n]);
return 0;
}
购票
不知道为什么是黑,裸的斜率优化,倍增找一下边界,树剖线段树套个李超线段树就行了。
难度远小于上一道。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 2e5+5,M = 1e6;
const LL inf = 1e18;
int n,T;
LL l[N],p[N],q[N],f[N];
int head[N],tot,fa[40][N];
struct E {int u,v; LL w;} e[N<<1];
inline void add(int u,int v,LL w) {e[++tot]={head[u],v,w}; head[u]=tot;}
namespace LC
{
int tot,num;
struct L
{
LL k,b;
inline LL K(int x) {return k*x+b;}
} lin[N];
struct T {int l,r,v;} tr[N<<6];
inline void mdf(int &k,int l,int r,int v)
{
if(!k) return tr[k=++num].v=v,void(0);
if(l==r) return lin[v].K(l)<lin[tr[k].v].K(l)?(tr[k].v=v,void(0)):void(0);
int mid=l+r>>1;
lin[v].K(mid)<lin[tr[k].v].K(mid)?swap(v,tr[k].v):void(0);
if(lin[v].K(l)<lin[tr[k].v].K(l)) mdf(tr[k].l,l,mid,v);
if(lin[v].K(r)<lin[tr[k].v].K(r)) mdf(tr[k].r,mid+1,r,v);
}
inline LL que(int k,int l,int r,int p)
{
if(!k) return inf;
if(l==r) return lin[tr[k].v].K(p);
int mid=l+r>>1;
return min(lin[tr[k].v].K(p),(p<=mid?que(tr[k].l,l,mid,p):que(tr[k].r,mid+1,r,p)));
}
}
namespace SEG
{
int rt[N<<2];
inline void mdf(int k,int l,int r,int p,int v)
{
LC::mdf(rt[k],0,M,v);
if(l==r) return;
int mid=l+r>>1;
if(p<=mid) mdf(k<<1,l,mid,p,v);
else mdf(k<<1|1,mid+1,r,p,v);
}
inline LL que(int k,int l,int r,int L,int R,int p)
{
if(l>=L&&r<=R) return LC::que(rt[k],0,M,p);
int mid=l+r>>1;
if(R<=mid) return que(k<<1,l,mid,L,R,p);
else if(L>mid) return que(k<<1|1,mid+1,r,L,R,p);
else return min(que(k<<1,l,mid,L,R,p),que(k<<1|1,mid+1,r,L,R,p));
}
}
namespace HDK
{
int sz[N],son[N],top[N],dfn[N],rk[N],num,dep[N]; LL d[N];
void dfs1(int u)
{
sz[u]=1; son[u]=-1; dep[u]=dep[fa[0][u]]+1;
for(int i=1;i<=20;i++) fa[i][u]=fa[i-1][fa[i-1][u]];
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v;
d[v]=d[u]+e[i].w; dfs1(v); sz[u]+=sz[v];
if(son[u]==-1||sz[son[u]]<sz[v]) son[u]=v;
}
}
void dfs2(int u,int t)
{
dfn[u]=++num; rk[num]=u; top[u]=t;
if(son[u]==-1) return;
dfs2(son[u],t);
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v; if(v==son[u]) continue;
dfs2(v,v);
}
}
inline LL quepath(int x,int y,int p)
{
LL res=inf;
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]]) swap(x,y);
res=min(res,SEG::que(1,1,n,dfn[top[x]],dfn[x],p));
x=fa[0][top[x]];
}
if(dfn[x]>dfn[y]) swap(x,y);
res=min(res,SEG::que(1,1,n,dfn[x],dfn[y],p));
return res;
}
inline int get(int x,LL l)
{
for(int i=20;i>=0;i--) if(fa[i][x]&&d[x]-d[fa[i][x]]<=l) l-=(d[x]-d[fa[i][x]]),x=fa[i][x];
return x;
}
void work(int u)
{
if(u!=1)
{
int v=get(u,l[u]);
f[u]=quepath(fa[0][u],v,p[u])+d[u]*p[u]+q[u];
}
LC::lin[++LC::tot]={-d[u],f[u]};
SEG::mdf(1,1,n,dfn[u],LC::tot);
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v;
work(v);
}
}
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d",&n,&T);
for(int i=2;i<=n;i++)
{
LL x; scanf("%d%lld%lld%lld%lld",&fa[0][i],&x,&p[i],&q[i],&l[i]);
add(fa[0][i],i,x);
}
LC::lin[0]={0,inf};
HDK::dfs1(1); HDK::dfs2(1,1);
HDK::work(1);
for(int i=2;i<=n;i++) printf("%lld\n",f[i]);
return 0;
}
等差
下标从 \(0\) 开始的数组,每次加入一个数,询问加入这个数后,是否存在 \(k\) 使每一个 \((a_j,a_{j+k},\dots)_{j=0}^{k-1}\) 都是一个等差数列。
哈希 trick。
先发现合法的 \(k\) 是单增的,然后容易发现每一个合法的 \(k\) 都有一个管辖区间,左端点是 \(2k-1\),只要找到右端点就好了。
问题在于怎么 check,考虑我们是对两个区间整体相减,所以可以直接用 hash 搞定,单次复杂度 \(O(\frac{n}{k})\),由于 \(k\) 是单增的,总复杂度 \(O(n \log n)\),当然远远卡不到上界。
code
#include<bits/stdc++.h>
using namespace std;
#define ULL unsigned long long
const int N = 2e6+5,B = 233;
#define LL long long
int a[N],m,c[N],b[N];
ULL hs[N],p[N];
inline ULL get(int l,int r) {return hs[r]-hs[l-1]*p[r-l+1];}
inline bool check(int l,int r,int k) {return get(l,r)-get(l-k,r-k)==get(l-k,r-k)-get(l-2*k,r-2*k);}
inline bool check(int n,int k)
{
for(int i=k*2+1;i<=n;i+=k) if(!check(i,min(n,i+k-1),k)) return 0;
return 1;
}
int main()
{
freopen("arithmetic.in","r",stdin);
freopen("arithmetic.out","w",stdout);
scanf("%d",&m); p[0]=1;
for(int i=1;i<=m;i++) p[i]=p[i-1]*B;
int fl=1;
for(int n=1;n<=m;n++)
{
int x; scanf("%d",&x);
a[n]=x; hs[n]=hs[n-1]*B+a[n];
if(fl*2<n&&!check((n-1)/fl*fl+1,n,fl)) while(!check(n,++fl));
putchar('0'+(2*fl+1<=n));
}
return 0;
}
叉积
给出 \(n\) 个向量 \((x_i,y_i)_{i=1}^{n}\),每次询问给出一个向量 \((x_p,y_p)\),询问 \(\sum_{i=l}^{r} (x_p,y_p) \times (x_i,y_i)\) 的最大值(最大子段叉积)
叉积的式子是 \(\sum_{i=l}^{r} x_p \times y_i - y_p \times x_i\),化一下就是 \(x_p (\sum y_i -\frac{y_p}{x_p}\sum x_i )\),发现这是个斜率优化的问题,思考发现李超线段树不可做,于是开始考虑凸包。(好像不是凸包而是凸壳,但是作者包壳不分)
首先判掉 \(x_p\) 是 \(0\) 的情况,剩下的相当于要在凸包中插入 \(n^2\) 个点,然后就可以指针扫求答案。
但是直接插入 \(n^2\) 个点显然是不现实的,首先将向量做前缀和,那么我们需要加入所有 \((x_i-x_j,y_i-y_j)_{0 \le j \lt i \le n }\),考虑分治。
这个不就是所有左区间对右区间的贡献吗?暴力加显然是不行,那么开始学习新科技:闵可夫斯基和!!!
我们当然只在乎凸包上的点,而闵可夫斯基和就是将两个凸包直接加在一起。(如下图)
合并方法也给出:
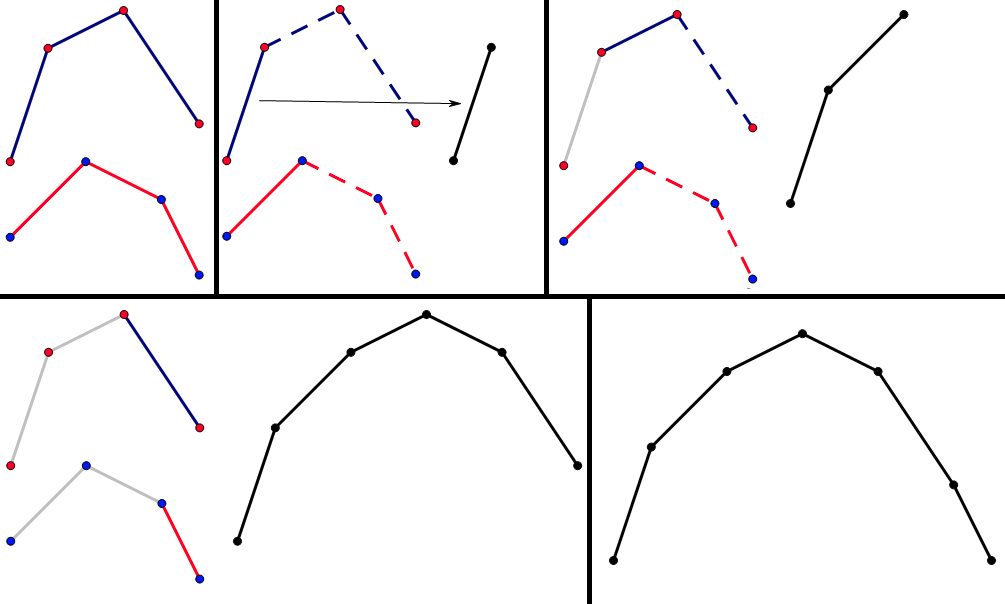
图都来自 wqs二分&闵可夫斯基和学习笔记,讲的非常好。
起点是两个凸包的起点相加,后面每次选斜率较大的一条边加进去。
求闵可夫斯基和就等价于我们求出所有向量的和再建出凸包。
对于本题对于每一个区间维护过中点的区间和形成的凸包,根据上文的前缀和和闵可夫斯基和可以简单求出。
这些凸包上的点总共最多有 \(O(n\log n)\) 个,直接暴力合并成一个大凸包即可。
最后根据 \(x_p\) 的正负,需要维护一个上凸包和下凸包,离线双指针扫即可。
还有区间查询的进阶版,留给 KTT 用脚维护,不需要任何脑子
多写函数,不太难写,据说 Jijidawang 还有超麻烦的做法。
code
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define P pair<vector<A>,vector<A>>
#define V(x) vector<x>
#define LL long long
const int N = 1e5+5;
int n,m;
struct A
{
LL x,y;
inline A(LL _x=0,LL _y=0) {x=_x; y=_y;}
inline A operator + (const A &X) const {A res; res=A(X.x+x,X.y+y); return res;}
inline A operator - (const A &X) const {A res; res=A(x-X.x,y-X.y); return res;}
} a[N],st[N],tmp[N];
struct Q {int id; LL x,y;} q[N*10];
V(A) UC,DC;
inline long double K (const A &x,const A &y) {return (long double)(y.y-x.y)/(y.x-x.x);}
inline long double K (const Q &x) {return (long double)x.y/x.x;}
LL ans[N*10];
inline void debug(V(A) x) {for(auto &y:x) printf("%lld %lld\n",y.x,y.y); putchar('\n');}
namespace Convex
{
inline void Sort(int l,int r,int mid)
{
int i=l,j=mid+1,t=0;
for(;i<=mid;i++)
{
while(j<=r&&a[j].x<a[i].x) tmp[++t]=a[j],j++;
tmp[++t]=a[i];
}
while(j<=r) tmp[++t]=a[j],j++;
for(int i=r;i>=l;i--) a[i]=tmp[t--];
}
inline V(A) bui(const V(A) &x,bool fl)
{
if(x.size()<=2) return x;
V(A) res; int sz=x.size(),top=0;
st[++top]=x[0]; st[++top]=x[1];
for(int i=2;i<sz;i++)
{
if(fl) {while(top>1&&K(st[top-1],st[top])<=K(st[top],x[i])) top--;}
else {while(top>1&&K(st[top-1],st[top])>=K(st[top],x[i])) top--;}
st[++top]=x[i];
}
for(int i=1;i<=top;i++) res.push_back(st[i]);
return res;
}
inline V(A) add(const V(A) &x,const V(A) &y,bool fl)
{
if(x.empty()) return y;
if(y.empty()) return x;
V(A) res;
int l=0,r=0,top=0,szx=x.size(),szy=y.size();
res.push_back(x[l++]+y[r++]),top++;
for(;l<szx;l++)
{
if(fl) {while(r<szy&&K(y[r-1],y[r])>K(x[l-1],x[l])) res.push_back(res[top-1]+(y[r]-y[r-1])),r++,top++;}
else {while(r<szy&&K(y[r-1],y[r])<K(x[l-1],x[l])) res.push_back(res[top-1]+(y[r]-y[r-1])),r++,top++;}
res.push_back(res[top-1]+(x[l]-x[l-1])),top++;
}
while(r<szy) res.push_back(res[top-1]+(y[r]-y[r-1])),r++,top++;
return res;
}
inline void unq(V(A) &x,bool fl)
{
V(A) res; A tmp; int sz=x.size();
for(int i=0;i<sz;i++)
{
tmp=x[i];
while(i+1<sz&&x[i+1].x==x[i].x) fl?tmp.y=max(tmp.y,x[i+1].y):tmp.y=min(tmp.y,x[i+1].y),i++;
res.push_back(tmp);
}
x=res;
}
inline void init(int l,int r)
{
V(A) res1,res2;
if(l==r) return;
int mid=l+r>>1;
init(l,mid); init(mid+1,r);
V(A) L1,R1,L2,R2; A tmp1,tmp2;
for(int i=mid;i>=l;i--)
{
tmp1=tmp2=a[i];
while(i-1>=l&&a[i].x==a[i-1].x) tmp1.y=max(tmp1.y,a[i-1].y),tmp2.y=min(tmp2.y,a[i-1].y),i--;
L1.push_back(A(-tmp2.x,-tmp2.y));
L2.push_back(A(-tmp1.x,-tmp1.y));
}
for(int i=mid+1;i<=r;i++)
{
tmp1=tmp2=a[i];
while(i+1<=r&&a[i].x==a[i+1].x) tmp1.y=max(tmp1.y,a[i+1].y),tmp2.y=min(tmp2.y,a[i+1].y),i++;
R1.push_back(tmp1);
R2.push_back(tmp2);
}
L2=bui(L2,0); R2=bui(R2,0); L1=bui(L1,1); R1=bui(R1,1);
res1=add(L1,R1,1); res2=add(L2,R2,0);
for(auto &x:res1) UC.push_back(x);
for(auto &x:res2) DC.push_back(x);
Sort(l,r,mid);
}
} using namespace Convex;
inline LL read()
{
LL res=0; char x=getchar(); bool fl=0;
while(x<'0'||x>'9') {if(x=='-') fl=1; x=getchar();}
while(x>='0'&&x<='9') res=(res<<1)+(res<<3)+(x^48),x=getchar();
return fl?-res:res;
}
int main()
{
freopen("cross.in","r",stdin);
freopen("cross.out","w",stdout);
scanf("%d%d",&n,&m);
memset(ans,-0x7f,sizeof(ans));
LL mi=0,x1=0,x2=0,mx=0;
for(int i=1;i<=n;i++)
{
a[i].x=read(); a[i].y=read(); a[i].x+=a[i-1].x,a[i].y+=a[i-1].y;
x1=max(x1,a[i].x-mi); x2=min(x2,a[i].x-mx);
mx=max(mx,a[i].x); mi=min(mi,a[i].x);
}
init(0,n);
sort(UC.begin(),UC.end(),[&](const A &x,const A &y){return x.x<y.x;});
sort(DC.begin(),DC.end(),[&](const A &x,const A &y){return x.x<y.x;});
unq(UC,1); unq(DC,0);
UC=bui(UC,1); DC=bui(DC,0);
int tot=0;
for(int i=1;i<=m;i++)
{
LL x=read(),y=read();
if(x==0) ans[i]=max(-y*x1,-y*x2);
else q[++tot]={i,x,y};
}
sort(q+1,q+tot+1,[&](const Q &x,const Q &y){return K(x)>K(y);});
int l=0,r=0,szx=UC.size(),szy=DC.size();
for(int i=1;i<=tot;i++)
{
while(l<szx-1&&K(UC[l],UC[l+1])>=K(q[i])) l++;
ans[q[i].id]=max(ans[q[i].id],q[i].x*UC[l].y-q[i].y*UC[l].x);
}
sort(q+1,q+tot+1,[&](const Q &x,const Q &y){return K(x)<K(y);});
for(int i=1;i<=tot;i++)
{
while(r<szy-1&&K(DC[r],DC[r+1])<=K(q[i])) r++;
ans[q[i].id]=max(ans[q[i].id],q[i].x*DC[r].y-q[i].y*DC[r].x);
}
for(int i=1;i<=m;i++) printf("%lld\n",ans[i]);
return 0;
}
ABC388F
玛丽还是太弱了。
发现性质 \(A,B\) 很小,先把长度大于等于 \(B\) 的区间判掉,剩下的区间长度一定都小于 \(B\)。
既然都这么小了,那直接暴力是不是就行了?
一个长度大于 \(400\) 的空地可以直接缩掉,因为走到这一段的最右端的时候一定是连续的一段(\(B^2 \le 400\))。
因此考虑缩点(直接缩,而不是用指针扫,前者要好写的多),最多有 \(4 \times 10\) 个点,直接暴力就行。
对于可以走的区间可以差分做,也很妙。
注意缩点的前提是 \(A \ne B\),所以特判 \(A = B\) 的情况。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 2e5+5;
LL n,l[N],r[N],cs;
bool vs[N*500];
int d[N*500],m,A,B;
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%lld%d%d%d",&n,&m,&A,&B);
for(int i=1;i<=m;i++) scanf("%lld%lld",&l[i],&r[i]);
if(A==B)
{
bool fl=!((n-1)%A);
for(int i=1;i<=m;i++)
{
if(r[i]-l[i]+1>=B) return printf("No\n"),0;
for(LL j=l[i];j<=r[i];j++) if((j-1)%A==0) return printf("No\n"),0;
}
fl?(printf("Yes\n")):(printf("No\n"));
}
else
{
for(int i=1;i<=m;i++)
{
int tmp=min(400ll,l[i]-r[i-1]-1);
cs+=tmp;
if(r[i]-l[i]+1>=B) return printf("No\n"),0;
for(int j=1;j<=r[i]-l[i]+1;j++) vs[++cs]=1;
}
cs+=min(400ll,n-r[m]);
d[1]=1; d[2]=-1;
for(int i=1;i<=cs;i++)
{
d[i]+=d[i-1];
if(d[i]&&!vs[i]) d[i+A]++,d[i+B+1]--;
}
d[cs]?(printf("Yes\n")):(printf("No\n"));
}
return 0;
}
ABC373F
好题。
Sol 1
学习了单调队列优化多重背包。
简单来说,对于某个物品,重量为 \(w\),价值为 \(v\),有 \(s\) 个。
那么转移形如 \(f_i = \max \{ f_{i-k \times w}+k \times v\}\)。
我们可以将 \(i\) 按对 \(w\) 的余数分组,那么对于这个物品来说,每组之间的转移可以看做独立的。
所以状态就变成 \(f_{j+a \times w} = \max \{ f_{j+b \times w} +(a-b) \times v\}\)。
拆一下就变成了 \(f_{j+a \times w} = \max \{ f_{j+b \times w} -b \times v +a \times v \}\)
我们用单调队列维护前面的 \(f_{j+b \times w} -b \times v\),就可以了。
如果个数 \(\gt s\),那么就把队首弹出。
对于本题仍考虑这样做,那就是 \(f_{j+a\times w}=\max \{ g_{j+b\times w}+(a-b) \times v -(a-b)^2 \}\)
拆开就是 \(b^2 - g_b +b \times v = a \times 2b +a \times v -a^2 -f_a \ , (f_a=f_{j+a\times w},g_b=g_{j+b\times w})\)。
然后直接斜率优化就对了
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 3e3+5;
#define y(x) (1ll*x*x+1ll*x*v[i]-g[x*w[i]+j])
#define x(x) (2ll*x)
int n,m,v[N],w[N];
LL f[N],g[N];
int l,r,q[N];
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d%d",&w[i],&v[i]);
for(int i=1;i<=n;i++)
{
if(w[i]>m||v[i]<=0) continue;
for(int j=0;j<w[i];j++)
{
l=r=1; q[1]=0;
for(int k=1;k*w[i]+j<=m;k++)
{
while(l<r&&(y(q[r])-y(q[r-1]))*(x(k)-x(q[r]))>=(y(k)-y(q[r]))*(x(q[r])-x(q[r-1]))) r--;
q[++r]=k;
while(l<r&&y(q[l+1])-y(q[l])<=k*(x(q[l+1])-x(q[l]))) l++;
f[k*w[i]+j]=1ll*x(q[l])*k+1ll*k*v[i]-1ll*k*k-y(q[l]);
}
}
for(int j=0;j<=m;j++) g[j]=f[j];
}
printf("%lld\n",f[m]);
return 0;
}
Sol2
另外官方的好做法,对于物品,选第 \(i\) 个增加的贡献就是 \(v-2 \times i+1\)。
所以对于同一重量的物品,我们可以用优先队列维护选 \(j\) 个的最大值。
然后重量就是严格单增的了,那么 dp 复杂度就是 \(O(nm\ln m)\) 的。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 3e3+5;
int n,m,w[N];
struct A {int w,v;} a[N];
LL f[N],g[N][N];
priority_queue<int> q[N];
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d%d",&a[i].w,&a[i].v);
int cnt=0;
sort(a+1,a+1+n,[&](const A &x,const A &y){return x.w==y.w?x.v<y.v:x.w<y.w;});
for(int i=1;i<=n;i++)
{
if(a[i].w!=a[i-1].w) w[++cnt]=a[i].w;
q[cnt].push(a[i].v-1);
}
n=cnt;
for(int i=1;i<=n;i++)
{
for(int j=1;j*w[i]<=m;j++)
{
LL sum=q[i].top(); q[i].pop();
if(sum<=0) break;
g[i][j]=g[i][j-1]+sum;
q[i].push(sum-2);
}
}
for(int i=1;i<=n;i++)
for(int j=m;j>=0;j--)
for(int k=1;k*w[i]<=j&&g[i][k];k++)
f[j]=max(f[j],f[j-k*w[i]]+g[i][k]);
printf("%lld\n",f[m]);
return 0;
}
枇杷树
题面

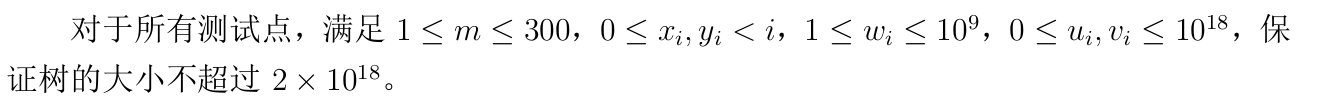
好不容易赛时想出来了。。。
总点数是 \(2 \times 10^{18}\) 的,但是发现只关心那些交界处的关键点即可,而关键点是 \(300\) 的。
那么我们只需要考虑两棵树合并的时候多了哪些贡献就好了。
首先是新加的边,会有 \(sz_x \times sz_y \times w\) 的贡献,
对于 \(x\) 内的每一条边,增加的贡献就是 \(sz_y \times w_i \times sz_i\),其中 \(sz_i\) 是以 \(u\) 为根子树 \(i\) 的大小,\(w_i\) 是 \(i\) 的父向边。
发现 \(w_i \times sz_i\) 可以直接维护,每次增加的就是 \(sz_y \times dis_{u,i}\),\(dis\) 也可以 \(m^2\) 处理。\(y\) 同理。
总时间复杂度 \(O(m^3)\)。
然后就 \(\mathbb{T}\) 飞了,因为用 unordered_map 存 \(m^3\) 太艰难了,换成 \(gb_hash\) 就 \(\mathbb{M}\) 了。
玄学(我觉得很玄学)记搜就可以,因为远远卡不到上界。但理论复杂度是一样的啊!
code
#include<bits/stdc++.h>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/hash_policy.hpp>//用hash
using namespace std;
using namespace __gnu_pbds;
#define unordered_map gp_hash_table
const int N = 505,mod = 1e9+7;
#define LL long long
int m,x[N],y[N],c[N];
LL u[N],v[N],w[N],sz[N],ans[N];
LL g[N][N];
unordered_map<LL,int> mp[N];
unordered_map<LL,LL> f[N];
unordered_map<LL,unordered_map<LL,int> > d[N];
inline void ins(int u,LL d)
{
if(mp[u][d]) return;
mp[u][d]=1;
g[u][++c[u]]=d;
if(x[u]&&d<sz[x[u]]) ins(x[u],d);
if(y[u]&&d>=sz[x[u]]) ins(y[u],d-sz[x[u]]);
}
inline LL read()
{
LL res=0; char x=getchar();
while(x<'0'||x>'9') x=getchar();
while(x>='0'&&x<='9') res=(res<<1)+(res<<3)+(x^48),x=getchar();
return res;
}
inline LL dis(LL i,LL x,LL y)
{
if(x>y) swap(x,y);
if(x==y) return 0;
if(d[i][x][y]) return d[i][x][y];
else if(x>=sz[::x[i]]) return d[i][x][y]=dis(::y[i],x-sz[::x[i]],y-sz[::x[i]]);
else if(y<sz[::x[i]]) return d[i][x][y]=dis(::x[i],x,y);
else return d[i][x][y]=(dis(::x[i],x,u[i])+dis(::y[i],y-sz[::x[i]],v[i])+w[i])%mod;
}
int main()
{
freopen("loquat.in","r",stdin);
freopen("loquat.out","w",stdout);
scanf("%d",&m); sz[0]=1;
mp[0][0]=1; g[0][++c[0]]=0;
for(int i=1;i<=m;i++)
{
x[i]=read(); y[i]=read(); u[i]=read(); v[i]=read(); w[i]=read();
ins(x[i],u[i]); ins(y[i],v[i]); sz[i]=sz[x[i]]+sz[y[i]];
}
for(int i=1;i<=m;i++)
{
int x=::x[i],y=::y[i];
LL szx=sz[x]%mod,szy=sz[y]%mod;
ans[i]=(ans[x]+ans[y])%mod;
ans[i]=(ans[i]+szy*szx%mod*w[i]%mod)%mod;
ans[i]=(ans[i]+szy*f[x][u[i]]%mod+szx*f[y][v[i]]%mod)%mod;
for(int j=1;j<=c[x];j++)
{
LL a=g[x][j];
f[i][a]=(f[x][a]+f[y][v[i]])%mod;
f[i][a]=(f[i][a]+szy*w[i]%mod+dis(x,a,u[i])*szy%mod)%mod;
}
for(int j=1;j<=c[y];j++)
{
LL a=g[y][j];
f[i][a+sz[x]]=(f[y][a]+f[x][u[i]])%mod;
f[i][a+sz[x]]=(f[i][a+sz[x]]+szx*w[i]%mod+dis(y,a,v[i])*szx%mod)%mod;
}
}
for(int i=1;i<=m;i++) printf("%lld\n",ans[i]);
return 0;
}
上古遗迹
区间最大广告牌(能看懂?)
如果全局直接单调栈,现在是区间询问,换一种思路。
应该是一个很典的吧。
仍然是单调栈维护每个点的管辖范围,得到很多线段,询问也是一些线段,考虑类似扫描线。
离线,树状数组做掉询问完全包含或被包含的情况。
剩下的考虑有交的贡献,分为两种,即询问在右边和询问在左边。
讨论询问在右边时,对于询问 \((ql,qr)\),线段 \(\{(l,r),h\}\)(\(ql \le l \le qr \le r\)),
对于线段来说,左端点是确定的,右端点是 \(qr\),并且要满足 \(qr \le r\)。
贡献是 \(h\times qr + h\times l + h\)。发现是一个一次函数,那么直接将线段当成线段(乐)插进李超中,然后询问就是查询横坐标。
询问在左边 \(l \le 1l \le r \le qr\) 时同理。
线段插李超是 \(O(\log^2 n)\) 的,先在线段树上定位区间,然后在区间中插入。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 2e5+5;
int n,m,a[N],l[N],r[N],tot;
int st[N],top;
struct Q {int id,l,r,v;} q[N<<1];
LL ans[N];
LL c[N];
inline void mdf(int x,LL v,bool fl) {for(;x&&x<=n;x+=fl?-(x&-x):(x&-x)) c[x]=max(c[x],v);}
inline LL que(int x,bool fl) {LL res=0; for(;x&&x<=n;x-=fl?-(x&-x):(x&-x)) res=max(res,c[x]); return res;}
inline bool cmp1(const Q &x,const Q &y){return x.l==y.l?(x.id<y.id):(x.l<y.l);}
inline bool cmp2(const Q &x,const Q &y){return x.l==y.l?(x.id<y.id):(x.l>y.l);}
inline bool cmp3(const Q &x,const Q &y){return x.r==y.r?(x.id<y.id):(x.r<y.r);}
namespace LC
{
struct Line
{
LL k,b;
inline Line(LL _k=0,LL _b=0){k=_k; b=_b;}
inline LL K(int x){return k*x+b;}
} lin[N<<1];
int tr[N<<2];
inline void ins(int k,int l,int r,int v)
{
if(l==r) return lin[tr[k]].K(l)<lin[v].K(l)?tr[k]=v,void(0):void(0);
int mid=l+r>>1;
lin[tr[k]].K(mid)<lin[v].K(mid)?swap(tr[k],v):void(0);
if(lin[tr[k]].K(l)<lin[v].K(l)) ins(k<<1,l,mid,v);
if(lin[tr[k]].K(r)<lin[v].K(r)) ins(k<<1|1,mid+1,r,v);
}
inline void mdf(int k,int l,int r,int L,int R,int v)
{
if(l>=L&&r<=R) return ins(k,l,r,v);
int mid=l+r>>1;
if(L<=mid) mdf(k<<1,l,mid,L,R,v);
if(R>mid) mdf(k<<1|1,mid+1,r,L,R,v);
}
inline LL que(int k,int l,int r,int p)
{
if(l==r) return lin[tr[k]].K(p);
int mid=l+r>>1;
return max(lin[tr[k]].K(p),p<=mid?que(k<<1,l,mid,p):que(k<<1|1,mid+1,r,p));
}
} using namespace LC;
int main()
{
freopen("relics.in","r",stdin);
freopen("relics.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=n+1;i++)
{
while(top&&a[i]<a[st[top]])
{
r[st[top]]=i-1; top--;
}
st[++top]=i;
}
top=0;
for(int i=n;i>=0;i--)
{
while(top&&a[i]<a[st[top]])
{
l[st[top]]=i+1; top--;
}
st[++top]=i;
}
for(int i=1;i<=n;i++) q[++tot]={0,l[i],r[i],a[i]};
for(int i=1;i<=m;i++)
{
int x,y; scanf("%d%d",&x,&y);
q[++tot]={i,x,y,0};
}
sort(q+1,q+1+tot,cmp1);
for(int i=1;i<=tot;i++)//l<=ql<=qr<=r
{
if(q[i].id) ans[q[i].id]=max(ans[q[i].id],1ll*(q[i].r-q[i].l+1)*que(q[i].r,1));
else mdf(q[i].r,q[i].v,1);
}
memset(c,0,sizeof(c));
sort(q+1,q+1+tot,cmp2);
for(int i=1;i<=tot;i++)
{
if(q[i].id) ans[q[i].id]=max(que(1,1,n,q[i].r),ans[q[i].id]);
else
{
lin[i]={1ll*q[i].v,1ll*q[i].v-1ll*q[i].v*q[i].l};
mdf(1,1,n,q[i].l,q[i].r,i);
}
}
memset(tr,0,sizeof(tr));
for(int i=1;i<=tot;i++)//ql<=l<=r<=qr
{
if(q[i].id) ans[q[i].id]=max(ans[q[i].id],que(q[i].r,0));
else mdf(q[i].r,1ll*q[i].v*(q[i].r-q[i].l+1),0);
}
sort(q+1,q+1+tot,cmp3);
for(int i=1;i<=tot;i++)
{
if(q[i].id) ans[q[i].id]=max(que(1,1,n,q[i].l),ans[q[i].id]);
else
{
lin[i]={-1ll*q[i].v,1ll*q[i].v+1ll*q[i].v*q[i].r};
mdf(1,1,n,q[i].l,q[i].r,i);
}
}
for(int i=1;i<=m;i++) printf("%lld\n",ans[i]);
return 0;
}
吞天得手
对 \(2^n-1\) 个子序列求字典序前 \(k\) 小的子序列的哈希值。\(n,k,a_i \le 10^5\)。
膜拜神 sto sto sto xrlong
能想到开优先队列,分层跑,但是具体实现有些困难,也想不到 dfs 直接做,
第一个状态肯定是最小的数(可能不止一个),然后考虑扩展。
第一次肯定是找它后面第一小的,然后作为一个长度为二的状态(可能有很多个),再向后找,直到找不到了。
第一小的找完了再找第二小的。
我们按长度分层,那么上面其实只有两种操作,一种是递归到下一层,另一种是在本层中移动。
那么可以把当前已有的状态作为分层标准,后面要找谁作为这一层内的排序标准。
同一层内的状态就形如 \(1\1\1 \to 2\)、\(1\1\1 \to 3\),前面都是一样的,只有最后一个后继状态作为评判标准。
后面第 \(k\) 小可以在主席树上查。
然后直接 dfs 就做完了。学习了神的构造函数写法。学习了神用主席树上的一个值同时表示位置和权值的方法。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
#define PQ(x) priority_queue<x>
const int N = 1e5+5,M = 1e6,mod = 998244353;
const LL V = 1ll*M*N+N;
int n,k,b,a[N],ans[N],tot,rt[N];
namespace HJT
{
int tot;
struct T {int l,r,sz;} tr[N<<6];
inline void pushup(int k) {tr[k].sz=tr[tr[k].l].sz+tr[tr[k].r].sz;}
inline void mdf(int &k,int pk,LL l,LL r,LL p)
{
k=++tot; tr[k]=tr[pk];
if(l==r) return tr[k].sz++,void(0);
LL mid=l+r>>1;
if(p<=mid) mdf(tr[k].l,tr[pk].l,l,mid,p);
else mdf(tr[k].r,tr[pk].r,mid+1,r,p);
pushup(k);
}
inline LL que(int k,LL l,LL r,int kk)
{
if(!k) return 0;
if(l==r) return l;
LL mid=l+r>>1;
if(tr[tr[k].l].sz>=kk) return que(tr[k].l,l,mid,kk);
else return que(tr[k].r,mid+1,r,kk-tr[tr[k].l].sz);
}
}
struct A
{
int l,hs,k,p,pv;
inline A(int a,int b):l(a),hs(b),k(1)
{
assert(k<=n-l);
LL tmp=HJT::que(rt[l+1],1,V,k);
pv=tmp/N; p=tmp%N;
}
inline bool operator < (const A &x) const {return pv>x.pv;}
inline bool nxt()
{
if(k+1>n-l) return 0;
++k;
assert(k<=n-l);
LL tmp=HJT::que(rt[l+1],1,V,k);
p=tmp%N; pv=tmp/N;
return 1;
}
};
inline void print(int x)
{
printf("%d\n",x); if(!--k) exit(0);
}
void dfs(PQ(A) &q)
{
while(!q.empty())
{
PQ(A) s;
A u=q.top();
while(!q.empty()&&q.top().pv==u.pv)
{
A v=q.top(); q.pop();
if(v.l+1<=n)
{
int hs=(1ll*v.hs*b+v.pv)%mod;
print(hs);
if(v.p+1<=n) s.emplace(v.p,hs);
}
if(v.nxt()) q.emplace(v);
}#include<bits/stdc++.h>
using namespace std;
#define LL long long
#define PQ(x) priority_queue<x>
const int N = 1e5+5,M = 1e6,mod = 998244353;
const LL V = 1ll*M*N+N;
int n,k,b,a[N],ans[N],tot,rt[N];
namespace HJT
{
int tot;
struct T {int l,r,sz;} tr[N<<6];
inline void pushup(int k) {tr[k].sz=tr[tr[k].l].sz+tr[tr[k].r].sz;}
inline void mdf(int &k,int pk,LL l,LL r,LL p)
{
k=++tot; tr[k]=tr[pk];
if(l==r) return tr[k].sz++,void(0);
LL mid=l+r>>1;
if(p<=mid) mdf(tr[k].l,tr[pk].l,l,mid,p);
else mdf(tr[k].r,tr[pk].r,mid+1,r,p);
pushup(k);
}
inline LL que(int k,LL l,LL r,int kk)
{
if(!k) return 0;
if(l==r) return l;
LL mid=l+r>>1;
if(tr[tr[k].l].sz>=kk) return que(tr[k].l,l,mid,kk);
else return que(tr[k].r,mid+1,r,kk-tr[tr[k].l].sz);
}
}
struct A
{
int l,hs,k,p,pv;
inline A(int a,int b):l(a),hs(b),k(1)
{
assert(k<=n-l);
LL tmp=HJT::que(rt[l+1],1,V,k);
pv=tmp/N; p=tmp%N;
}
inline bool operator < (const A &x) const {return pv>x.pv;}
inline bool nxt()
{
if(k+1>n-l) return 0;
++k;
assert(k<=n-l);
LL tmp=HJT::que(rt[l+1],1,V,k);
p=tmp%N; pv=tmp/N;
return 1;
}
};
inline void print(int x)
{
printf("%d\n",x); if(!--k) exit(0);
}
void dfs(PQ(A) &q)
{
while(!q.empty())
{
PQ(A) s;
A u=q.top();
while(!q.empty()&&q.top().pv==u.pv)
{
A v=q.top(); q.pop();
if(v.l+1<=n)
{
int hs=(1ll*v.hs*b+v.pv)%mod;
print(hs);
if(v.p+1<=n) s.emplace(v.p,hs);
}
if(v.nxt()) q.emplace(v);
}
dfs(s);
}
}
int main()
{
freopen("ttds.in","r",stdin);
freopen("ttds.out","w",stdout);
scanf("%d%d%d",&n,&k,&b);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=n;i>=1;i--) HJT::mdf(rt[i],rt[i+1],1,V,1ll*N*a[i]+i);
PQ(A) q; q.emplace(0,0);
dfs(q);
return 0;
}
dfs(s);
}
}
int main()
{
freopen("ttds.in","r",stdin);
freopen("ttds.out","w",stdout);
scanf("%d%d%d",&n,&k,&b);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=n;i>=1;i--) HJT::mdf(rt[i],rt[i+1],1,V,1ll*N*a[i]+i);
PQ(A) q; q.emplace(0,0);
dfs(q);
return 0;
}
trick:n 个点的 lca,按 dfn 排序,最后一个和第一个。
排列

听了好几遍也不理解怎么在笛卡尔树上 dp,其实从插入的角度考虑更好理解吧。
每次只会保留较大值,所以不妨枚举较大值,一个个插进去。
插入其实就是合并左右子区间的过程,对于子区间分别记录它两端的状态:
-
左端点是否紧挨着边界。
-
右端点是否紧挨着边界。
其中边界指 \(0\) 或 \(n+1\) 的位置,因为从小到大填,所以如果不是边界那么必然比区间内所有数都大。
设计状态 \(f_{i,j,0/1,0/1}\) 表示填 \(i\) 个数(区间长度为 \(i\)),清空(或剩一个)最多需要 \(j\) 步。
如果是 \(f_{i,j,0,0}\),表示左右紧挨边界,那么最后会剩下插进去的最大值,所以由 \(f_{k-1,j,0,1}\) 和 \(f_{i-k,j,1,0}\) 转移(左右都清空,就只剩下一个了)。
如果是 \(f_{i,j,1,0}\),则需要用 \(f_{i,j-1,1,1}\) 转移,左右都有更大值,所以完全清空需要 \(j-1\) 时,新插入的才能恰好在第 \(j\) 步被消掉。
如果是 \(f_{i,j,1,1}\),如果左右区间都恰好用了 \(j\) 步才消完,那么实际被消掉的时刻是 \(j+1\),所以要减去左右区间恰好都用 \(j\) 步的情况。
对于上述每一种情况,都需要乘上 \(\binom{i-1}{k-1}\) 的转移系数。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
#define fi first
#define se second
const int N = 1e3+5;
inline int read()
{
int res=0; char x=getchar();
while(x>'9'||x<'0') x=getchar();
while(x<='9'&&x>='0') res=(res<<1)+(res<<3)+(x^48),x=getchar();
return res;
}
#define A(x) (x>=mod?x-mod:x)
int f[N][15][2][2],n,m,c[N][N],mod;
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
n=read(); m=read(); mod=read();
if(m>=15) return printf("0\n"),0;
for(int i=0;i<=m;++i) f[0][i][0][0]=f[0][i][0][1]=f[0][i][1][0]=f[0][i][1][1]=1;
for(int i=0;i<=n;++i)
{
c[i][0]=c[i][i]=1;
for(int j=1;j<i;j++) c[i][j]=A(c[i-1][j]+c[i-1][j-1]);
}
for(int i=1;i<=n;++i)
{
for(int j=1;j<=m;++j)
{
for(int k=1;k<=i;++k)
{
f[i][j][0][0]=A(f[i][j][0][0]+1ll*f[k-1][j][0][1]*f[i-k][j][1][0]%mod*c[i-1][k-1]%mod);
f[i][j][1][0]=A(f[i][j][1][0]+1ll*f[k-1][j-1][1][1]*f[i-k][j][1][0]%mod*c[i-1][k-1]%mod);
f[i][j][0][1]=A(f[i][j][0][1]+1ll*f[k-1][j][0][1]*f[i-k][j-1][1][1]%mod*c[i-1][k-1]%mod);
int t1=A(f[k-1][j][1][1]-f[k-1][j-1][1][1]+mod),t2=A(f[i-k][j][1][1]-f[i-k][j-1][1][1]+mod);
f[i][j][1][1]=A(f[i][j][1][1]+(1ll*f[k-1][j][1][1]*f[i-k][j][1][1]-1ll*t1*t2%mod+mod)%mod*c[i-1][k-1]%mod);
}
}
}
printf("%d\n",A(f[n][m][0][0]-f[n][m-1][0][0]+mod));
return 0;
}
丁香之路
好题。
题意:完全图,边权为 \(|u-v|,\)给定 \(m\) 条边必须经过,求 \(s\) 到 \(i\) 的最短路径。
可能是 trick 吧,如果把 \(m\) 条边单独拿出来建图就是求至少添加多少条边存在欧拉路。
欧拉路要求起点和终点度数为奇数,剩下都为偶数,我们可以连上 \(s\) 和 \(i\) 变成欧拉回路问题(弱化问题)。
注意只是度数改变,并不需要实际连边。
问题变成在 \(m+1\) 条边中最少加入多少条边存在欧拉回路。
结论:先保证度数再维护连通性一定不劣。
感性理解:只需要考虑维护连通性的边恰好连接了两个度数为奇数的点,这时这条边本身的作用就是保证度数了。
注意边权有性质,我们不妨只连 \(i \to i+1\) 的边,那么相邻的连接一定更优,从小到大扫所有度数为奇数的点,然后连边。
将连通块缩起来,然后对每两个块之间最近的点加边跑最小生成树,为了不影响度数,树边要算两边。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 2.5e3+5,M = 3.2e6+5;
int n,m,s,d[N],fa[N],bl[N],tot;
LL ans,sum;
inline int find(int x) {return x==fa[x]?x:fa[x]=find(fa[x]);}
struct E {int u,v,w;} e[M];
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d%d",&n,&m,&s);
for(int i=1;i<=n;i++) fa[i]=i;
for(int i=1;i<=m;i++)
{
int x,y; scanf("%d%d",&x,&y);
sum+=abs(x-y);
d[x]++; d[y]++;
fa[find(x)]=find(y);
}
for(int i=1;i<=n;i++) bl[i]=find(i);
for(int o=1;o<=n;o++)
{
for(int i=1;i<=n;i++) fa[i]=i;
d[s]++; d[o]++;
ans=sum; int pre=0; tot=0;
fa[find(bl[s])]=find(bl[o]);
for(int i=1;i<=n;i++)
if(d[i]&1)
{
if(pre)
{
ans+=i-pre;
for(int j=pre;j<=i;j++) fa[find(bl[j])]=find(bl[pre]);
pre=0;
}
else pre=i;
}
assert(pre==0);
for(int i=1;i<=n;i++)
if(d[i])
{
if(pre&&find(bl[pre])!=find(bl[i])) e[++tot]={bl[pre],bl[i],abs(i-pre)};
pre=i;
}
sort(e+1,e+1+tot,[&](const E &x,const E &y){return x.w<y.w;});
for(int i=1;i<=tot;i++)
if(find(e[i].u)!=find(e[i].v)) ans+=2*e[i].w,fa[find(e[i].u)]=find(e[i].v);
d[s]--; d[o]--;
printf("%lld ",ans);
}
return 0;
}
CF868F
这我学个锤子啊
学习分治 dp。
想了 XXX 年的数据结构优化 dp,最后是决策单调性???
朴素暴力 \(f_{i,j}=\min(f_{k,j-1}+w(k+1,i))\),考虑 \(w(i,j)\) 有决策单调性。
证明: \(w(i,j)+w(i+1,j+1)-w(i+1,j)-w(i,j+1) = -[a_i==a_{j+1}] \le 0\)。所以满足四边形不等式,所以有决策单调性。
然后类似整体二分的形式进行 dp,记录两个区间,一个是决策点区间,一个是被决策点区间。被决策点每次取区间的中点,指针在决策区间扫。
具体计算贡献类比莫队,因为指针在每层只会移动 \(O(n)\) 次,所以复杂度不变。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
#define fi first
#define se second
const int N = 1e5+5;
int n,m,a[N];
LL f[25][N],now=0;
int cl=1,cr=0,cnt[N];
inline LL w(int l,int r)
{
if(l==cl&&r==cr) return now;
while(cl>l) --cl,now+=cnt[a[cl]]++;
while(cr<r) cr++,now+=cnt[a[cr]]++;
while(cl<l) now-=--cnt[a[cl]],cl++;
while(cr>r) now-=--cnt[a[cr]],cr--;
return now;
}
inline void dp(int l,int r,int L,int R,int p)
{
if(l>r) return;
int mid=l+r>>1,k=L; LL mi=f[p-1][L]+w(L+1,mid);
for(int i=L+1;i<=min(mid-1,R);i++) if(mi>f[p-1][i]+w(i+1,mid)) mi=f[p-1][i]+w(i+1,mid),k=i;
f[p][mid]=mi;
dp(l,mid-1,L,k,p); dp(mid+1,r,k,R,p);
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d",&n,&m);
memset(f,0x3f,sizeof(f));
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=n;i++) f[1][i]=w(1,i);
for(int i=2;i<=m;i++) dp(1,n,1,n,i);
printf("%lld\n",f[m][n]);
return 0;
}
原根



 浙公网安备 33010602011771号
浙公网安备 33010602011771号