AT/CF
ABC374 E
最大最小值,想到二分,问题是怎么 check。
其实就是对两个种有价值有重量的物品,求达到规定价值的最小重量。
只有两种物品,而且数据范围很小,考虑贪心。
假设 \(a\) 的性价比较高,\(b\) 的性价比较低,那么不可能选太多 \(b\)。
也就是如果能用 \(a\) 代替的就用 \(a\) 代替。所以选 \(b\) 的总价值不能超过 \(lcm(a,b)\)。否则能用 \(a\) 替换更优。
发现 \(a\) 最大只有 \(100\),所以 \(b\) 最多选 \(100\) 个。暴力枚举。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 105;
int n; LL X;
int a[N],b[N],p[N],q[N];
bool check(int w)
{
LL sum=0;
for(int i=1;i<=n;i++)
{
LL tmp=1e18;
for(int j=0;j<=100;j++)
{
int k=ceil((1.0*w-j*b[i])/a[i]); k=max(k,0);
tmp=min(tmp,1ll*k*p[i]+1ll*j*q[i]);
if(j*b[i]>w) break;
}
sum+=tmp;
}
return sum<=X;
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%lld",&n,&X);
for(int i=1;i<=n;i++)
{
scanf("%d%d%d%d",&a[i],&p[i],&b[i],&q[i]);
if(a[i]*q[i]<b[i]*p[i]) swap(q[i],p[i]),swap(a[i],b[i]);
}
int l=0,r=1e9+7,ans=0;
while(l<=r)
{
int mid=(1ll*r-l>>1)+l;
if(check(mid)) ans=mid,l=mid+1;
else r=mid-1;
}
printf("%d\n",ans);
return 0;
}
CF997 C2
有点难调。
容易发现是否合法只与 \(a\) 的元素在 \(b\) 中第一次出现的位置有关。
对于 \(a\) 序列来说,在 \(b\) 中的第一次出现的位置应该是单调递增的。
所以直接用 set 维护位置,每次更新就行。(不需要特殊处理第一个位置)
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
int T;
const int N = 2e5+5;
int n,m,q;
int a[N],b[N],ys[N];
set<int> p[N];
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&T);
while(T--)
{
scanf("%d%d%d",&n,&m,&q);
for(int i=1;i<=n;i++) scanf("%d",&a[i]),p[a[i]].clear(),p[a[i]].insert(m+1),ys[a[i]]=i;
for(int i=1;i<=m;i++)
{
scanf("%d",&b[i]);
}
for(int i=1;i<=m;i++)
{
p[b[i]].insert(i);
}
int res=0;
for(int i=2;i<=n;i++) if(*p[a[i]].begin()<*p[a[i-1]].begin())
res++;
if(!res) printf("YA\n");
else printf("TIDAK\n");
while(q--)
{
int x,y; scanf("%d%d",&x,&y);
if(ys[b[x]]-1>=1&&*p[b[x]].begin()<*p[a[ys[b[x]]-1]].begin())
res--;
if(ys[b[x]]+1<=n&&*p[a[ys[b[x]]+1]].begin()<*p[b[x]].begin())
res--;
p[b[x]].erase(x);
if(ys[b[x]]-1>=1&&*p[b[x]].begin()<*p[a[ys[b[x]]-1]].begin())
res++;
if(ys[b[x]]+1<=n&&*p[a[ys[b[x]]+1]].begin()<*p[b[x]].begin())
res++;
if(ys[y]-1>=1&&*p[y].begin()<*p[a[ys[y]-1]].begin())
res--;
if(ys[y]+1<=n&&*p[a[ys[y]+1]].begin()<*p[y].begin())
res--;
p[y].insert(x);
if(ys[y]-1>=1&&*p[y].begin()<*p[a[ys[y]-1]].begin())
res++;
if(ys[y]+1<=n&&*p[a[ys[y]+1]].begin()<*p[y].begin())
res++;
b[x]=y;
if(res==0) printf("YA\n");
else printf("TIDAK\n");
}
}
}
CF997 E1
出题人贴心地给出了 \(n^3\) 的范围。直接考虑 floyd。
跑完最短路后暴力枚举选的点就好,仍然是 \(n^3\) 暴力。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
int T;
const int N = 405;
int n,m,q;
int f[N][N],a[N],now[N],ttt[N];
LL sum;
bool vs[N];
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&T);
while(T--)
{
sum=0;
scanf("%d%d%d",&n,&m,&q);
memset(vs,0,sizeof(vs));
memset(f,0x3f,sizeof(f));
for(int i=1;i<=q;i++) scanf("%d",&a[i]);
for(int i=1;i<=m;i++)
{
int x,y,z; scanf("%d%d%d",&x,&y,&z);
f[x][y]=f[y][x]=z;
}
for(int i=1;i<=n;i++) f[i][i]=0;
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
f[i][j]=min(f[i][j],max(f[i][k],f[k][j]));
int fl=0;
sum=1e18;
for(int i=1;i<=n;i++)
{
LL tmp=0;
for(int j=1;j<=q;j++) tmp+=f[i][a[j]];
if(sum>tmp)
{
for(int j=1;j<=q;j++) now[j]=f[i][a[j]];
sum=tmp; fl=i;
}
}
vs[fl]=1;
printf("%lld ",sum);
for(int i=2;i<=n;i++)
{
if(i>=q) {printf("0 "); continue;}
fl=0;
for(int j=1;j<=q;j++) ttt[j]=now[j];
for(int j=1;j<=n;j++) if(!vs[j])
{
LL tmp=0;
for(int k=1;k<=q;k++) tmp+=min(f[j][a[k]],now[k]);
if(tmp<sum)
{
for(int k=1;k<=q;k++) ttt[k]=min(f[j][a[k]],now[k]);
sum=tmp; fl=j;
}
}
for(int j=1;j<=q;j++) now[j]=ttt[j];
vs[fl]=1; printf("%lld ",sum);
}
putchar('\n');
}
}
CF997 E2
要求 \(n^2\) 的复杂度,发现问题是求路径上最大边权的最小值。考虑Kruskal 生成树。
其实这个生成的是一个堆,将边权转化为点权,保证父亲的权值不小于儿子。
因此我们将问题转化为了树上问题,设计状态 \(f_{u,i}\) 表示以 \(u\) 为根的子树内有 \(i\) 个 servers。
从下向上更新,由于越往上权值越大,说明需要连接的最大边越大,所以需要连接的点一定尽量连深的点。
如果是 \(f_{son,0}\),说明儿子这棵子树内没有 servers,那么如果以 \(u\) 根这棵子树内有servers(\(f_{u,1/2/3\dots}\)),那么一定连这个更优。
此时最大边就是 \(va_u\)(根节点的权值),用子树内需要连接的点的个数(\(cnt_{son}\)) 乘上最大边就行。
如果以儿子为根的子树内已经有了,那直接相加更新就好。(\(f_{u,i+j}=\sum_i\sum_j f_{son_1,i}+f_{son_2,j}\))
然后你发现重构树会使点数翻倍,空间直接炸。
小 trick,发现最终答案只关心根 \(f_{1,i}\),所以 dp 数组用 vector,每更新完一个就返还空间,shrink_to_fit。
code
#include<bits/stdc++.h>
using namespace std;
int T;
#define LL long long
const int N = 1e4+5;
const LL inf = 1e15;
int n,m,q;
int num;
struct E {int u,v,w;} ed[N];
int fa[N],son[N][2],va[N],cnt[N];
inline int find(int x) {return x==fa[x]?(x):(fa[x]=find(fa[x]));}
vector<LL> f[N];
void dfs(int u)
{
if(!son[u][0]&&!son[u][1]) return ;
dfs(son[u][0]); dfs(son[u][1]);
f[u].resize(cnt[u]+1,inf);
for(int i=1;i<=cnt[son[u][1]];i++) f[u][i]=min(f[u][i],1ll*va[u]*cnt[son[u][0]]+f[son[u][1]][i]);
for(int i=1;i<=cnt[son[u][0]];i++) f[u][i]=min(f[u][i],1ll*va[u]*cnt[son[u][1]]+f[son[u][0]][i]);
for(int i=1;i<=cnt[son[u][0]];i++)
for(int j=1;j<=cnt[son[u][1]];j++)
f[u][i+j]=min(f[u][i+j],f[son[u][0]][i]+f[son[u][1]][j]);
f[son[u][0]].clear(); f[son[u][0]].shrink_to_fit();
f[son[u][1]].clear(); f[son[u][1]].shrink_to_fit();
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&T);
while(T--)
{
scanf("%d%d%d",&n,&m,&q);
for(int i=1;i<=n<<1;i++)
{
f[i].clear(); f[i].resize(1,inf);
cnt[i]=0; fa[i]=i; son[i][0]=son[i][1]=0;
}
for(int i=1,x;i<=q;i++) scanf("%d",&x),cnt[x]=1,f[x].resize(2,inf),f[x][1]=0;
for(int i=1;i<=m;i++)
scanf("%d%d%d",&ed[i].u,&ed[i].v,&ed[i].w);
num=n;
sort(ed+1,ed+1+m,[&](E &x,E &y){return x.w<y.w;});
for(int i=1;i<=m;i++)
{
int fx=find(ed[i].u),fy=find(ed[i].v);
if(fx==fy) continue;
fa[fx]=fa[fy]=++num; va[num]=ed[i].w;
son[num][0]=fx; son[num][1]=fy; cnt[num]=cnt[fx]+cnt[fy];
}
dfs(num);
for(int i=1;i<=q-1;i++) printf("%lld ",f[num][i]);
for(int i=q;i<=n;i++) printf("0 ");
putchar('\n');
}
return 0;
}
ABC374F
思路来自 int_R
假设物品发出时间是 \(s_i\),需求时间是 \(t_i\),那么答案就是 \(\sum s - \sum t\),发现后面是定值,可以直接处理。
我们要确定的就是所有物品发出时间的总和。
在能出发的时刻,要不然立即出发,要不然等下一个时刻出发,所以出发时间一定是 \(t_i+kx\),也就是从某一个 \(t_i\) 开始后连续发送几次 \(x\),然后等待。
设计状态 \(f_{i,j}\) 表示在 \(t_i\),第 \(i\) 个物品的状态从即将出发到已经到达,此时还有 \(j\) 个物品没有出发(被跳过去了)。
转移即枚举这次运输会连续几个 \(x\),注意细节。
马蜂抽象。
code
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 105,inf = 1e15;
int n,k,x,t[N],f[N][N],ans;
main()
{
freopen("in.in","r",stdin);
freopen("out.out","w",stdout);
scanf("%lld%lld%lld",&n,&k,&x);
memset(f,0x3f,sizeof(f)); f[0][0]=0;
for(int i=1;i<=n;i++) scanf("%lld",&t[i]),ans-=t[i];
for(int i=1;i<=n;i++)//第 i-1 个到了,第 i 个将要发出时,还有 j 个没发出
{
for(int j=0;j<i;j++) f[i][j]=min(f[i-1][j],f[i][j]);
for(int j=i;j>=1;j--) f[i][j]=f[i][j-1]; f[i][0]=inf;//第 i 个没发出,要加上。
for(int j=1;j<=i;j++)
{
int now=j,tm=t[i],sum=0,h=i+1;
while(now)
{
int cur=min(now,k);
sum+=cur*tm; now-=cur; tm+=x;//发第 i 个。
for(;h<=n&&t[h]<tm;h++) now++;
f[h][now]=min(f[h][now],f[i][j]+sum);//第 i 个发完,该第 h 个了。
}
}
}
printf("%lld\n",ans+f[n+1][0]);
return 0;
}
ABC375E
唐完了。。。
显然背包,发现数据范围较小,直接爆开四维 \(f_{i,j,k,h}\) 表示前 \(i\) 个物品,三组分别为 \(j,k,h\) 的最小交换次数,每个物品分讨放到哪组。
当然四维开不下,记录前缀和,把最后一维删掉,然后就做完了。
(WwW)
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 105;
int aim,n,v[N],s[N];
int pos[N];
int f[105][1505][1505],ans;
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&n);
memset(f,0x3f,sizeof(f));
for(int i=1;i<=n;i++) scanf("%d%d",&pos[i],&v[i]),s[i]=s[i-1]+v[i];
if(s[n]%3) return printf("%d\n",-1),0;
aim=s[n]/3;
f[0][0][0]=0;
for(int i=1;i<=n;i++)
{
for(int j=0;j<=s[i];j++)
{
for(int k=0;k<=s[i]-j;k++)
{
if(j>=v[i]) f[i][j][k]=min(f[i-1][j-v[i]][k]+(pos[i]!=1),f[i][j][k]);
if(k>=v[i]) f[i][j][k]=min(f[i-1][j][k-v[i]]+(pos[i]!=2),f[i][j][k]);
if(s[i]-k-j>=v[i]) f[i][j][k]=min(f[i-1][j][k]+(pos[i]!=3),f[i][j][k]);
}
}
}
if(f[n][aim][aim]<=1e9) printf("%d\n",f[n][aim][aim]);
else printf("-1\n");
return 0;
}
ABC373E
有点ex。
二分,然后考虑 check。
思路很简单,代码很抽象,还是太蔡了。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
#define P pair<LL,int>
#define fi first
#define se second
const int N = 2e5+5;
int n,m;
LL k,s[N],ans[N];
P a[N];
bool check(LL mid,int p)
{
int ls=n-m+1-(p>=n-m+1);//(要算上自己)
int rs=lower_bound(a+ls,a+1+n,make_pair(a[p].fi+mid+1,0))-a-1;//(小于等于的个数)
return ((rs-ls+1)*(a[p].fi+mid+1)-(s[rs]-s[ls-1]))-(mid+1)*(p>=n-m+1)>k-mid;//(注意最后要减去自己的贡献)
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d%lld",&n,&m,&k);
if(m==n)
{
for(int i=1;i<=n;i++) printf("%d ",0); putchar('\n');
return 0;
}
for(int i=1;i<=n;i++) scanf("%lld",&a[i].fi),a[i].se=i;
sort(a+1,a+1+n);
for(int i=1;i<=n;i++) s[i]=s[i-1]+a[i].fi;
k=k-s[n];
for(int i=1;i<=n;i++)
{
LL l=0,r=k+1,res=0;
while(l<=r)
{
LL mid=l+r>>1;
if(check(mid,i)) res=mid,r=mid-1;
else l=mid+1;
}
if(res==k+1) ans[a[i].se]=-1;
else ans[a[i].se]=res;
}
for(int i=1;i<=n;i++) printf("%lld ",ans[i]); putchar('\n');
return 0;
}
CF932E
数学题,想当年 5k 讲的时候听都听不懂,没想到现在能自己颓了……
没有高级定理,trick 化成递推,其中有一步很妙:
然后发现一下递推时 \(k\) 很小,然后做完了。
注意记搜时用 unordered_map 会 \(\mathbb{T}\),需要开数组加偏移量。
懒了,具体做法看 sto sto sto Qyun
ABC365E
QY 推的题,按位扫描线记录奇偶的个数。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 2e5+5;
int n,a[N],c[30];
LL ans;
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int j=0;j<=27;j++) c[j]=(a[1]>>j)&1;
for(int i=2;i<=n;i++)
for(int j=0;j<=27;j++)
if((a[i]>>j)&1) ans+=1ll*(i-1-c[j])*(1<<j),c[j]=i-c[j];
else ans+=1ll*c[j]*(1<<j);
printf("%lld\n",ans);
return 0;
}
ABC365F
有点难,想不到。
容易想到:能向右走就向右走,直到碰到墙,贴墙走,然后可能又走一段直线,然后又贴墙走,循环。。。
第一次碰墙的位置可以二分,需要 ST 表维护区间最大/小值。
如果某一次贴墙后,下次一定是从上/下端点出发,后面的路径就确定了,可以预处理。
发现是路径问题,考虑图论连边,将每个端点看做一个节点,找到它向右走第一个碰壁的左/右端点(一定是离它较近的那个)。
有一个计算答案的小 trick,直接发现横向的代价一定是 \(R-L\),中间只需要记录纵向走了多少就行。
然后发现你肯定不能记录路径上每个点到每一个点的距离啊,查的时候也不能一个个跳吧。
所以想到这都是图了(实际上是棵树),直接倍增跳父亲,一直理解不了怎么想到倍增优化 dp,如果放到图上看会不会好一点。
然后倍增处理路径问题,中间的代价和可以用前缀和维护,注意细节处理,第一次和最后一次的贡献需要单独算。
回过头来看马,发现还挺简单的,你有了 jump 函数找第一次碰碰壁的位置,然后想到连边、倍增维护父亲,最后细节处理就是先跳一次,最后再手动跳一次,中间过程倍增直接自动化掉了。
code
#include<bits/stdc++.h>
using namespace std;
#define P pair<int,int>
#define fi first
#define se second
#define LL long long
const int N = 5e5+5;
int n,m,l[N],r[N],u[N],v[N],rk[N];
int mi[30][N],mx[30][N],lg[N],fa[30][N];
LL sum[N];
int head[N],tot,cnt;
struct E {int u,v,w;} e[N];
inline void add(int u,int v,int w) {e[++tot]={head[u],v,w}; head[u]=tot;}
inline int getmx(int l,int r)
{
int k=lg[r-l+1];
return max(mx[k][l],mx[k][r-(1<<k)+1]);
}
inline int getmi(int l,int r)
{
int k=lg[r-l+1];
return min(mi[k][l],mi[k][r-(1<<k)+1]);
}
inline int jum(int x,int p)
{
int l=x+1,r=n+1,res=l;
while(l<=r)
{
int mid=l+r>>1;
if(getmi(x,mid)>=p&&getmx(x,mid)<=p) l=mid+1;
else r=mid-1,res=mid;
}
return res;
}
void dfs(int u,int f)
{
fa[0][u]=f; for(int i=1;i<=25;i++) fa[i][u]=fa[i-1][fa[i-1][u]];
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v;
if(v==f) continue;
sum[v]=sum[u]+e[i].w; dfs(v,u);
}
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&n); lg[0]=-1;
for(int i=1;i<=n;i++) scanf("%d%d",&l[i],&r[i]),lg[i]=lg[i>>1]+1;
for(int i=1;i<=n;i++)
{
u[i]=++cnt; v[i]=++cnt; rk[cnt]=rk[cnt-1]=i;
mi[0][i]=r[i]; mx[0][i]=l[i];
} u[n+1]=v[n+1]=++cnt; rk[cnt]=n+1;
for(int i=1;i<=25;i++)
for(int j=1;j+(1<<i)-1<=n;j++)
mi[i][j]=min(mi[i-1][j],mi[i-1][j+(1<<i-1)]),
mx[i][j]=max(mx[i-1][j],mx[i-1][j+(1<<i-1)]);
for(int i=1;i<=n;i++)
{
int tmp=jum(i,r[i]);
if(tmp==n+1) add(u[n+1],u[i],0);
else if(r[i]>r[tmp]) add(u[tmp],u[i],r[i]-r[tmp]);
else add(v[tmp],u[i],l[tmp]-r[i]);
tmp=jum(i,l[i]);
if(tmp==n+1) add(v[n+1],v[i],0);
else if(l[i]>r[tmp]) add(u[tmp],v[i],l[i]-r[tmp]);
else add(v[tmp],v[i],l[tmp]-l[i]);
}
dfs(cnt,0);
scanf("%d",&m);
while(m--)
{
int x,y,L,R; scanf("%d%d%d%d",&L,&x,&R,&y);
if(L>R) swap(L,R),swap(x,y);
LL ans=R-L;
int tmp=jum(L,x);
if(tmp>=R) {printf("%lld\n",ans+abs(y-x)); continue;}
int be=0;
if(x>r[tmp]) be=u[tmp],ans+=x-r[tmp];
else be=v[tmp],ans+=l[tmp]-x;
L=tmp;
for(int i=25;i>=0;i--)
if(fa[i][be]&&rk[fa[i][be]]<=R)
ans+=sum[be]-sum[fa[i][be]],be=fa[i][be];
L=rk[be];
if(be==u[L]) ans+=abs(y-r[L]);
else ans+=abs(y-l[L]);
printf("%lld\n",ans);
}
}
ABC_dp_z
斜率优化板子,注意是 \(c(i)\) 而不是 \(c(q[i])\),被控好久。
好久不打斜率优化,每次打都现推还推不出来,可能理解会更深?
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 2e5+5;
int n,q[N],l,r;
LL k,f[N],a[N];
inline LL c(int i) {return f[i]+a[i]*a[i];}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%lld",&n,&k);
for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
l=1; r=1; f[1]=0; q[l]=1;
for(int i=2;i<=n;i++)
{
while(l<r&&c(q[l+1])-c(q[l])<=2*a[i]*(a[q[l+1]]-a[q[l]])) l++;
f[i]=f[q[l]]+(a[i]-a[q[l]])*(a[i]-a[q[l]])+k;
while(l<r&&(c(q[r])-c(q[r-1]))*(a[i]-a[q[r]])>=(c(i)-c(q[r]))*(a[q[r]]-a[q[r-1]])) r--;
q[++r]=i;
}
printf("%lld\n",f[n]);
return 0;
}
CF486D
树上 dp,感觉有点不像 dp。
给定范围,容易想到枚举一个极值,确定另一个的范围。
不要总想在状态中表示,你直接枚举,然后 \(O(n)\) dp 就做完了。注意去重。
dp 重点不只在设计状态和转移,还有如何转化为 dp。
update:注意数据范围!!!
code
#include<bits/stdc++.h>
using namespace std;
const int N = 2e3+5,mod = 1e9+7;
int n,d,a[N],mx,ans;
int head[N],tot;
struct E {int u,v;} e[N<<1];
inline void add(int u,int v) {e[++tot]={head[u],v}; head[u]=tot;}
int f[N];
vector<int> cnt[N];
int vs[N];
inline void dfs(int u,int fa,int now)
{
if(a[u]>now||a[u]<now-d) return;
f[u]=1;
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v; if(fa==v||vs[v]==now) continue;
dfs(v,u,now);
f[u]=(1ll*f[u]*(f[v]+1))%mod;
}
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%d",&d,&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]),cnt[a[i]].push_back(i),mx=max(mx,a[i]);
for(int i=1;i<n;i++)
{
int x,y; scanf("%d%d",&x,&y);
add(x,y); add(y,x);
}
for(int i=1;i<=mx;i++)
{
for(int j:cnt[i])
{
vs[j]=i;
dfs(j,0,i);
ans=(ans+f[j])%mod;
}
memset(f,0,sizeof(f));
}
printf("%d\n",ans);
return 0;
}
CF241B
Trie + 树上二分
很喵喵的 trick。
trick:将原序列排序后插入 Trie,原序列上的某一区间会经过 Trie 上的同一个节点(经过某一个树上节点的值一定是一段连续的区间),可以记录这个区间,维护一些信息。
这个 trick 好像可以解决一些可持久化问题,而且很常用。
在本题中,容易想到在树上二分求解。首先要找出第 \(k\) 大的值,然后对所有大于这个值的求和即可。
第 \(k\) 大值,我们可以二分,然后将每个数插进 Trie 中,找出大于当前二分值的个数。
当然这是 \(log^2\) 的,考虑能不能更优。
其实所有我们需要的信息都可以直接在树上维护,所以可以直接在树上二分。
考虑每个数在 Trie 搜索的过程可以反过来,维护所有数同时在树上搜索,实时维护每个值当前在树上所在的节点。
然后对于每一位统计每一个数通过异或能取到 \(1\) 的个数 \(cnt\),Trie 树维护 size 很容易。
-
如果 \(cnt>=m\),那么这一位一定要取到 \(1\)。
-
如果 \(cnt<m\),那么这一位取到 \(0\) 。
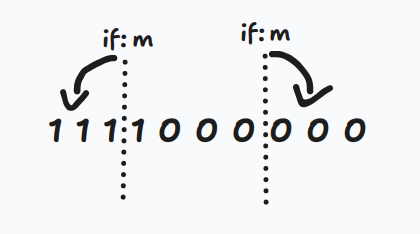
然后对于每一个值,按上面的结果对应地走到下一层。和线段树二分类似。最终找到第 \(m\) 大值 \(val\),复杂度 \(O(n\log n)\)。
每次向 \(0\) 走都要减去 \(m \gets m-cnt\),最后 \(m\) 会还有剩下的,是 \(val\) 的出现次数,可以直接统计答案。
然后考虑所有比 \(val\) 大的和怎么算。
首先仍然是对于每个值在 Trie 上一起跑,贴着较大的边界,如果 \(val\) 这一位是 \(0\),说明这里取 \(1\) 会产生比它大的,要统计贡献。
因为要求的是 \(a_i \oplus a_j\),\(a_i\) 是我们枚举的(在树上跑的)所以只需考虑所有能有贡献的 \(a_j\) 能提供的总贡献。
什么是能有贡献的 \(a_j\),也就是上文中 \(val\) 这一位是 \(0\) 的所有节点,经过这些节点的 \(a_j\)。
然后你发现了文章最前面写的 trick!!!
排序后记录每个节点管辖的区间,就可以很轻松的维护出有贡献的 \(a_j\),对于这些再按位枚举,我们统计 \(a_i \oplus a_j\) 的贡献。
发现一个区间问题!可以用前缀和维护每一位为 \(1/0\) 的个数,对于 \(a_i\) 相应求就行。
真的有人能看懂吗?感觉挺人类智慧的,但是又挺板。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 5e4+5,mod = 1e9+7;
int n,a[N],sum[35][N][2];
LL m;
inline LL qpow(LL a,int b)
{
LL res=1;
while(b)
{
if(b&1) res=res*a%mod;
a=a*a%mod; b>>=1;
}
return res;
}
namespace Trie
{
int son[N<<5][2],sz[N<<5],num,l[N<<5],r[N<<5],now[N],rt;
inline void ins(int x,int id)
{
if(!rt) rt=++num,l[rt]=1,r[rt]=n;
int now=rt; sz[now]++;
for(int i=30;i>=0;i--)
{
int c=(x>>i)&1;
if(!son[now][c]) son[now][c]=++num,l[son[now][c]]=id;
now=son[now][c]; sz[now]++; r[now]=id;
}
}
inline int get(LL &x)
{
int res=0;
for(int i=1;i<=n;i++) now[i]=rt;
for(int i=30;i>=0;i--)//1111100000 长这样,别想反了
{
LL cnt=0,to=0;
for(int j=1;j<=n;j++) cnt+=sz[son[now[j]][(a[j]>>i&1)^1]];
if(cnt>=x) res|=(1<<i),to=1;
else to=0,x-=cnt;
for(int j=1;j<=n;j++) now[j]=son[now[j]][(a[j]>>i&1)^to];
}
return res;
}
inline LL que(int l,int r,int v)
{
if(!l||!r) return 0;
LL res=0;
for(int i=30;i>=0;i--) res=(res+(1ll*sum[i][r][(v>>i&1)^1]-sum[i][l-1][(v>>i&1)^1])*(1ll<<i))%mod;
return res;
}
inline LL work(LL x)
{
int kth=get(x);
LL res=kth*x%mod;
for(int i=1;i<=n;i++) now[i]=rt;
for(int i=30;i>=0;i--)
{
int c=kth>>i&1;
if(!c) {for(int j=1;j<=n;j++) res=(res+que(l[son[now[j]][(a[j]>>i&1)^1]],r[son[now[j]][(a[j]>>i&1)^1]],a[j]))%mod;}
for(int j=1;j<=n;j++) now[j]=son[now[j]][(a[j]>>i&1)^c];
}
return res;
}
} using namespace Trie;
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%lld",&n,&m); m*=2;
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
sort(a+1,a+1+n);
for(int i=1;i<=n;i++) ins(a[i],i);
for(int i=1;i<=n;i++)
{
for(int j=30;j>=0;j--)
{
sum[j][i][0]=sum[j][i-1][0];
sum[j][i][1]=sum[j][i-1][1];
sum[j][i][a[i]>>j&1]++;
}
}
printf("%lld\n",work(m)*500000004ll%mod);
return 0;
}
CF1055F
异或路径做前缀和就变成上题的简单版了。
Trie 二分直接就做完了。
注意到出题人丧心病狂的卡空间。
学习 trick:Trie 滚存。
适用面应该很窄,因为本题是 Trie 有性质,可以对于每个二进制位一边插一边查。
所以只需要记录当前层每个数走到哪个节点就行了。
形象理解就是将 Trie 树数组隐藏的“深度”数组复现,然后再压掉。
抽象理解就是直接不建树,每个节点只维护两个指针,然后节点重复利用。
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 1e6+5;
int n;
LL a[N],k;
int head[N],tot,now[N];
struct E {int u,v; LL w;} e[N];
inline void add(int u,int v,LL w) {e[++tot]={head[u],v,w}; head[u]=tot;}
namespace Trie
{
int son[N<<2][2],sz[N<<2],p[N],cn;
inline LL que(LL k)
{
LL res=0;
for(int i=62;i>=0;i--)
{
for(int j=1;j<=n;j++)
{
int c=(a[j]>>i)&1;
if(!son[p[j]][c]) son[p[j]][c]=++cn;
p[j]=son[p[j]][c]; sz[p[j]]++;
}
LL cnt=0; int x=0;
for(int j=1;j<=n;j++) cnt+=sz[son[now[j]][(a[j]>>i)&1]];
if(cnt>=k) x=0;
else k-=cnt,res|=(1ll<<i),x=1;
for(int j=1;j<=n;j++) now[j]=son[now[j]][(a[j]>>i&1)^x];
for(int j=0;j<=cn;j++) son[j][0]=son[j][1]=0,sz[j]=0; cn=0;
}
return res;
}
} using namespace Trie;
void dfs(int u,LL d)
{
a[u]=d;
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v;
dfs(v,d^e[i].w);
}
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d%lld",&n,&k);
for(int i=2;i<=n;i++)
{
int x; LL y; scanf("%d%lld",&x,&y);
add(x,i,y);
}
dfs(1,0);
printf("%lld\n",que(k));
return 0;
}
CF490F
线段树合并
一句话题意:树上最长上升子序列。
需要维护向上和向下两个 dp 数组,然后每次合并更新答案。显然,要不然是 DSU,要不然线段树合并。
设 \(f_{u,i}\) 表示在 \(u\) 子树中以 \(i\) 结尾的最长上升子序列(指向根),\(g_{u,i}\) 表示在 \(u\) 子树中以 \(i\) 开始的最长上升子序列(指向叶子)。
在树上开值域线段树,维护 \(f,g\)。
在每个节点 \(lca\) 处合并子树内的信息,分为两种:
- 不选 lca
- 选 lca
先说不选 \(lca\),很妙的方法就是直接在合并过程中统计答案,对于线段树上每一个点,由 \(f\) 的左子树和 \(g\) 的右子树(或者反过来)合并得到。
类似的套路在之前的 曼哈顿转切比雪夫 也见过。
对于选 \(lca\) 的,在合并子树的过程中维护 \(f\) 和 \(g\) 的最大值,然后按序合并即可。
学会了一种新的线段树写法!!!
code
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+5;
int n,a[N],tl[N],cnt;
int head[N],tot,ans;
struct E {int u,v;} e[N<<1];
inline void add(int u,int v) {e[++tot]={head[u],v}; head[u]=tot;}
unordered_map<int,int> mp;
int g[N<<5],f[N<<5],num,rt[N];
struct T {int l,r;} tr[N<<5];
inline void mdf(int &k,int l,int r,int p,int v,int *va)
{
if(!k) k=++num;
va[k]=max(va[k],v);
if(l==r) return;
int mid=l+r>>1;
if(p<=mid) mdf(tr[k].l,l,mid,p,v,va);
else mdf(tr[k].r,mid+1,r,p,v,va);
}
inline int que(int k,int l,int r,int L,int R,int *va)
{
if(L>R) return 0;
if(!k) return 0;
if(l>=L&&r<=R) return va[k];
int mid=l+r>>1,res=0;
if(L<=mid) res=max(res,que(tr[k].l,l,mid,L,R,va));
if(R>mid) res=max(res,que(tr[k].r,mid+1,r,L,R,va));
return res;
}
inline void merge(int &x,int y)
{
if(!x||!y) return x=x|y,void(0);
ans=max(ans,f[tr[x].l]+g[tr[y].r]);
ans=max(ans,f[tr[y].l]+g[tr[x].r]);
merge(tr[x].l,tr[y].l);
merge(tr[x].r,tr[y].r);
f[x]=max(f[x],f[y]); g[x]=max(g[x],g[y]);
}
void dfs(int u,int fa)
{
int ff=0,gg=0;
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v; if(v==fa) continue;
dfs(v,u);
int tmp1=que(rt[v],1,cnt,1,a[u]-1,f);
int tmp2=que(rt[v],1,cnt,a[u]+1,cnt,g);
ans=max(ans,max(ff+tmp2+1,gg+tmp1+1));
ff=max(ff,tmp1); gg=max(gg,tmp2);
merge(rt[u],rt[v]);
}
mdf(rt[u],1,cnt,a[u],ff+1,f);
mdf(rt[u],1,cnt,a[u],gg+1,g);
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]),tl[++cnt]=a[i];
sort(tl+1,tl+1+cnt);
cnt=unique(tl+1,tl+1+cnt)-tl-1;
for(int i=1;i<=cnt;i++) mp[tl[i]]=i;
for(int i=1;i<=n;i++) a[i]=mp[a[i]];
for(int i=1;i<n;i++)
{
int x,y; scanf("%d%d",&x,&y);
add(x,y); add(y,x);
}
dfs(1,0);
printf("%d\n",ans);
return 0;
}
CF888G
学习菠萝包!
一道还算不错的菠萝题。
菠萝包一般用来处理边数很多的最小生成树问题(如完全图),本质和 KR 一样,通过在连通块间连边实现。
每次找到每个连通块的最小出边,加入这些边后至少会使连通块数量减半,所以是 \(log\) 级别的。
关键在于如何在完全图中快速的找到最小出边。
可以先参考这道题 星际联邦。
一句话题意:\(\forall i \lt j,w_{i,j}=a_j-a_i\),求 MST.
一句话题解:维护前缀最大值、和最大值不属于同一个连通块的次大值,菠萝。
同理,本题的关键就是求不属于同一个连通块的异或最大值。
显然想到 Trie,可以用全局 Trie “减去”(维护 size 做差)当前连通块,然后求最值。
Trie 合并和连通块合并注意顺序,调了好久。感觉菠萝包还是挺不好写的。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+5;
int fa[N];
inline int find(int x) {return x==fa[x]?(x):(fa[x]=find(fa[x]));}
int n,a[N],tmp[N],to[N];
long long ans;
namespace TRIE
{
int son[N*50][2],num,rt[N],sz[N*50],v[N*50];
inline void ins(int x,int r,int id)
{
if(!rt[r]) rt[r]=++num;
int now=rt[r];
for(int i=30;i>=0;i--)
{
int c=(x>>i)&1;
if(!son[now][c]) son[now][c]=++num;
now=son[now][c]; sz[now]++;
}
v[now]=id;
}
inline int merge(int x,int y)
{
if(!x||!y) return x|y;
son[x][0]=merge(son[x][0],son[y][0]);
son[x][1]=merge(son[x][1],son[y][1]);
sz[x]+=sz[y];
return x;
}
inline int que(int r1,int r2,int x)
{
r1=rt[r1]; r2=rt[r2]; int now1=r1,now2=r2;
for(int i=30;i>=0;i--)
{
int c=(x>>i)&1;
if(son[now1][c]&&sz[son[now1][c]]-sz[son[now2][c]]>0) now1=son[now1][c],now2=son[now2][c];
else now1=son[now1][c^1],now2=son[now2][c^1];
}
return v[now1];
}
} using namespace TRIE;
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
sort(a+1,a+1+n);
n=unique(a+1,a+1+n)-a-1;
for(int i=1;i<=n;i++) fa[i]=i,ins(a[i],0,i),ins(a[i],i,i);
int cnt=n;
while(cnt>1)
{
for(int i=0;i<=n;i++) tmp[i]=1e9;
for(int i=1;i<=n;i++)
{
int fx=find(i),t=que(0,fx,a[i]);
if((a[t]^a[i])<tmp[fx]) tmp[fx]=(a[t]^a[i]),to[fx]=t;
}
for(int i=1;i<=n;i++) if(tmp[find(i)]<1e9&&fa[i]!=find(to[fa[i]]))
ans+=tmp[fa[i]],cnt--,rt[fa[i]]=merge(rt[fa[i]],rt[fa[to[fa[i]]]]),fa[fa[to[fa[i]]]]=fa[i];
}
printf("%lld\n",ans);
return 0;
}
CF2023D
容易想到二分,容易想到在 check 中按值域从小到大枚举,容易想到最后就是求有向图可达性问题。
然后,不会啦!
发现有向图可达性不太可做(有向无环图最优应该只能做到 \(\frac{n^2}{\omega}\))。
你不用动脑子的发现你忽略了一些很重要的性质!
比如,这是棵内向基环树!!!
所以开始 ex 的分讨,分为环上和环上子树,两部分都可以通过维护有向 dep 做。
-
环上:为了方便找环,所以建无向边,但在环上实际判断时还需要判断方向,小心处理,维护环上 \(dep\)。
-
环上子树:在环上子树,为了确定两个点是否具有祖先关系,直接维护 dfs 序。然后用 \(dep\)
由于是内向树,子树之间一定不可达。
然后大力分讨就做完了!
code
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 1e6+5;
int T,a[N],n,b[N],m,t,bl[N],fa[N];
int head[N],tot;
struct E {int u,v;} e[N<<1];
inline void add(int u,int v) {e[++tot]={head[u],v}; head[u]=tot;}
inline int find(int x) {return fa[x]==x?(x):(fa[x]=find(fa[x]));}
unordered_map<int,bool> mp[N];
int st[N],top,h,dep[N],rt[N],in[N],num,out[N];
bool vs[N];
vector<int> cs[N];
inline void get(int u,int f,int rt)
{
st[++top]=u; vs[u]=1;
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v;
if(v==rt)
{
for(int j=1;j<=top;j++) cs[t].push_back(st[j]),bl[st[j]]=t; top--;
return;
}
if(vs[v]) continue;
get(v,u,rt);
}
--top;
}
void dfs1(int u,int f,int rt)
{
dep[u]=dep[f]+1;
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v;
if(v==rt) return;
if(bl[v]==bl[rt]&&b[v]==u) dfs1(v,u,rt);
}
}
inline void dfs(int u,int f)
{
dep[u]=dep[f]+1; bl[u]=t;
in[u]=++num;
for(int i=head[u];i;i=e[i].u)
{
int v=e[i].v; if(v==f||bl[v]) continue;
dfs(v,u);
}
out[u]=num;
}
inline int cir(int x,int y)
{
if(dep[x]>=dep[y]) return dep[x]-dep[y];
else return cs[bl[x]].size()-(dep[y]-dep[x]);
}
inline bool jd(int x,int len,int aim)
{
if(x==aim) return 1;
if(!bl[x]) x=b[x],len--; if(len<0) return 0;
if(x==aim) return 1;
if(!bl[aim]) return 0;
if(bl[x]==bl[aim])
{
if(bl[x]<=h) return cir(x,aim)<=len;
else
{
if(in[x]<in[aim]||in[x]>out[aim]) return 0;
return dep[x]-dep[aim]>=0?(dep[x]-dep[aim]<=len):(0);
}
}
else
{
if(bl[aim]<=h&&bl[x]>h&&bl[rt[bl[x]]]==bl[aim])
{
len-=dep[x]; x=rt[bl[x]];
if(dep[aim])
len-=cir(x,aim);
return len>=0;
}
else return 0;
}
}
bool check(int mid)
{
int l=1;
for(int i=1;i<=m;i++)
{
while(l<=n&&jd(a[l],mid,i)) l++;
if(l==n+1) break;
}
return l==n+1;
}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
scanf("%d",&T);
while(T--)
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=m;i++) scanf("%d",&b[i]),fa[i]=i,mp[i].clear(),cs[i].clear();
for(int i=1;i<=m;i++)
{
if(mp[b[b[i]]][b[i]]) continue;
add(b[b[i]],b[i]);
if(find(b[b[i]])==find(b[i])) t++,get(b[i],0,b[i]);
mp[b[b[i]]][b[i]]=1;
fa[b[i]]=fa[b[b[i]]];
}
h=t;
for(int i=1;i<=h;i++)
{
dfs1(cs[i][0],0,cs[i][0]);
for(int j:cs[i])
{
for(int k=head[j];k;k=e[k].u)
{
if(!bl[e[k].v]) ++t,rt[t]=j,dfs(e[k].v,0);
}
}
}
int l=0,r=m+1,res=0;
while(l<=r)
{
int mid=l+r>>1;
if(check(mid)) r=mid-1,res=mid;
else l=mid+1;
}
printf("%d\n",r==m+1?(-1):(res));
for(int i=1;i<=m;i++) dep[i]=0,vs[i]=0,bl[i]=0,head[i]=0; t=0; tot=0; num=0;
}
return 0;
}
CF2025E
我 dp 太菜啦!
数学方法这是个卡特兰数。但我们先不考虑。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号