对比学习损失函数InfoNCE

对比学习损失函数InfoNCE

在前文NCE损失函数将样本分为data和noise做二分类, InfoNCE将这种思想推广到多分类问题中, 使用Softmax形式推广, 我们回顾一下之前NCE的交叉熵损失函数, 在这里我们加上了负号, 让目标函数变成了损失函数, 如下公式所示:

\[\mathcal J_{NCE}=\sum_{t=1}^{k_d+k_n}\left[ D_t\log p_\theta(D=1|x_t,c_t)+(1-D_t)\log p_\theta(D=0|x_t,c_t)\right] \tag{Eq.1} \]

那么InfoNCE就是把后面这一坨东西推广成Softmax形式, 如下所示

\[\mathcal J_{InfoNCE}=\sum_{t=1}^{N}\left[\log\frac{\exp(u_\theta(x_t,c_t))}{\sum_{t'\in N}\exp(u_\theta(x_t,c_{t'}))}\right] \tag{Eq.2} \]

InfoNCE性质

开门见山讲, InfoNCE使用特征归一化可以让模型自带挖掘硬负样本的能力, 其次InfoNCE中负样本数量也是越多越好。

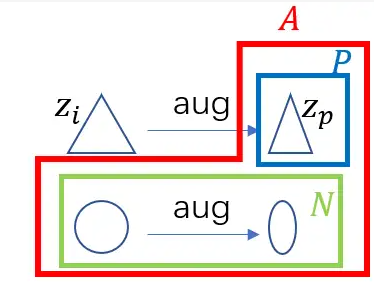
为了说明这两个性质, 我们需要额外讲解一些符号, 对于一个物品\(i\),数据增强后的结果为正样本集合, 用\(P\)表示(positive), 对于其他物品\(j\)以及它们的数据增强就是负样本集合, 用\(N\)表示(negative), 正样本和负样本集合合并在一起, 用\(A\)表示(all). 下面的图片可以更加直观的看到不同集合之间的关系:

我们为了计算简化, 具体化InfoNCE的表示, 直接使用归一化后的特征内积如下所示, 其中\(z_i\)是主任务学习到的归一化特征。

\[\mathcal L_{InfoNCE}=\sum_i\mathcal L_i=-\sum_i\log(\frac{\exp(z_iz_p/\tau)}{\sum_{a\in A}\exp(z_iz_a/\tau)}) \tag{Eq.3} \]

我们将Loss计算它对归一化特征的梯度, 计算过程如下：

\[\begin{aligned} \frac{\partial\mathcal L_i}{\partial z_i}&=-\frac{\partial}{\partial z_i}\log(\frac{\exp(z_iz_p/\tau)}{\sum_{a\in A}\exp(z_iz_a/\tau)}) \\ &= \frac{\partial}{\partial z_i}\left[\log\sum_{a\in A}\exp(z_iz_a/\tau)-{(z_iz_p/\tau)}\right] \\ &= \frac{\sum_{a\in A}(z_a/\tau)\exp(z_iz_a/\tau)}{\sum_{a\in A}\exp(z_iz_a/\tau)}-z_p/\tau \\ &= \frac{1}{\tau}\left[ \frac{\sum_{a\in A}z_a\exp(z_iz_a/\tau)}{\sum_{a\in A}\exp(z_iz_a/\tau)}-z_p\right] \end{aligned} \tag{Eq.4} \]

我们进一步整理上面的公式

\[\begin{aligned} \frac{\partial\mathcal L_i}{\partial z_i} &= \frac{1}{\tau}\left[ \frac{\sum_{a\in A}z_a\exp(z_iz_a/\tau)}{\sum_{a\in A}\exp(z_iz_a/\tau)}-z_p\right] \\ &=\frac{1}{\tau}\left[\frac{\sum_{n\in N}z_n\exp(z_iz_n/\tau)+z_p\exp(z_iz_p/\tau)}{\sum_{a\in A}\exp(z_iz_a/\tau)}-z_p\right] \\ &=\frac{1}{\tau}\left[z_p\left(\frac{\exp(z_iz_p/\tau)}{\sum_{a\in A}\exp(z_iz_a/\tau)} -1\right) + \sum_{n \in N}z_n\frac{\exp(z_iz_n/\tau)}{\sum_{a\in A}\exp(z_iz_a/\tau)}\right] \\ &=\frac{1}{\tau}\left[z_p(P_{ip}-1)+\sum_{n\in N}z_nP_{in}\right] \end{aligned} \tag{Eq.5} \]

我们分别使用\(P_{ip}\) 和 \(P_{in}\) 表示特征\(i\)的正样本在集合\(A\)中的概率，以及特征\(i\)的负样本在集合\(A\)中的概率。接着我们再计算归一化特征对未归一化特征\(w_i\) 的梯度，计算过程如下：

\[\frac{\partial z_i}{\partial w_i}=\frac{\partial}{\partial w_i}(\frac{w_i}{\|w_i\|})=\frac{1}{\|w_i\|}(I-\frac{w_iw_i^T}{\|w_i\|^2})=\frac{1}{\|w_i\|}(I-z_iz_i^T) \tag{Eq.6} \]

通过链式规则, 我们可以得到损失函数对未归一化特征\(w_i\)的梯度，结果如下

\[\frac{\partial\mathcal L_i}{\partial w_i}=\frac{\partial z_i}{\partial w_i}\frac{\partial\mathcal L_i}{\partial z_i}=\frac{1}{\tau\|w_i\|}(I-z_iz_i^T)\left[z_p(P_{ip}-1) + \sum_{n\in N}z_nP_{in}\right] \tag{Eq.7} \]

我们将\((I-z_iz_i^T)\)分配到后面，就可以得到正样本梯度\(P_{ip}\)的系数为\((I-z_iz_i^T)z_p\)，我们继续计算它的欧式大小：

\[\begin{aligned} \|(I-z_iz_i^T)z_p\|^2 &= [(I-z_iz_i^T)z_p]^T[(I-z_iz_i^T)z_p] \\ &= z_p^T(I-2z_iz_i^T+z_iz_i^Tz_iz_i^T)z_p \\ &= z_p^T(I-z_iz_i^T)z_p \\ &= z_p^Tz_p - z_p^Tz_izi^Tz_p \\ &= I - (z_i^Tz_p)^2 \end{aligned} \tag{Eq.8} \]

我们可以看到当我们物品\(i\)和它的正样本如果相似度太高 \((z_i^Tz_p) \approx 1\) , 那么这个系数就会趋于0, 几乎没有对梯度训练起作用, 如果和正样本的相似度不高, 这个系数就会趋于1, 对梯度训练起更大的作用. 所以我们可以看到归一化后的特征能让模型自带硬负样本挖掘的作用, 相似度高的样本不会对梯度起太大帮助.

其次我们可以看链式结果的正样本的梯度\(P_{ip}-1\) , 同理我们也可以看一下它的大小, 如下所示：

\[|P_{ip}-1| = \mid\frac{\exp(z_iz_p/\tau)}{\sum_{a\in A}\exp(z_iz_a/\tau)} -1\mid \propto |A| \tag{Eq.9} \]

我们可以看出它和\(A\)集合大小有很大关系. 这说明训练时的batchsize设置得越大, 取得的效果会更好