ddpm实际案例
ddpm实际案例
1.选择一个数据集
我们使用一个10000个数据的二位坐标特征的S字母作为数据集
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_s_curve
import torch
# 使用一个S图片作为数据
s_curve, _ = make_s_curve(10**4, noise=0.1)
s_curve = s_curve[:, [0,2]]/10.0
print("shape of moons:", np.shape(s_curve))
data = s_curve.T
fig, ax = plt.subplots()
ax.scatter(*data, color='red', edgecolor='white')
ax.axis('off')
dataset = torch.Tensor(s_curve).float()
shape of moons: (10000, 2)

2.确定超参数
假设T=100,betas是人为定义的递增数组
\[\alpha_t=1-\beta_t, \bar \alpha_t=\alpha_t\alpha_{t-1}...\alpha_1
\]
num_steps = 100
#确定beta
betas = torch.linspace(-6, 6, num_steps)
betas = torch.sigmoid(betas) * (0.5e-2 - 1e-5) + 1e-5
#计算alpha相关变量
alphas = 1- betas
alphas_prod = torch.cumprod(alphas, 0) #连乘alpha
alphas_bar_sqrt = torch.sqrt(alphas_prod)
one_minus_alphas_bar_sqrt = torch.sqrt(1 - alphas_prod)
assert alphas.shape == alphas_prod.shape == alphas_bar_sqrt.shape == one_minus_alphas_bar_sqrt.shape
print(betas.shape)
torch.Size([100])
3.前向过程的采样值
\[x_t=\sqrt{\bar \alpha_t}x_0+\sqrt{1-\bar\alpha_t}\epsilon_t,\epsilon_t\in\mathcal N(0,I)
\]
def q_x(x_0, t):
noise = torch.randn_like(x_0)
alphas_t = alphas_bar_sqrt[t]
alphas_1_m_t = one_minus_alphas_bar_sqrt[t]
return alphas_t * x_0 + alphas_1_m_t * noise
4.演示前向过程100步的效果
num_shows = 20
fig, axs = plt.subplots(2, 10, figsize=(28,3))
plt.rc('text', color='blue')
#一共10000个点,每个点包含两个坐标
#生成100步以内,每5步加噪的图像
for i in range(num_shows):
j = i // 10
k = i % 10
q_i = q_x(dataset, torch.tensor([i * num_steps//num_shows]))
axs[j, k].scatter(q_i[:,0], q_i[:, 1], color='red', edgecolor='white')
axs[j, k].set_axis_off()
axs[j, k].set_title('$q(\mathbf{x}_{'+ str(i * num_steps//num_shows) +'})$')

5.逆向过程的模型编写
# 一个简单的残差MLP模型用于Diffusion训练
import torch
import torch.nn as nn
# 用于训练ε_θ()的网络
class MLPDiffusion(nn.Module):
def __init__(self, n_steps, num_units=128):
super(MLPDiffusion, self).__init__()
self.linears = nn.ModuleList(
[
nn.Linear(2, num_units),
nn.ReLU(),
nn.Linear(num_units, num_units),
nn.ReLU(),
nn.Linear(num_units, num_units),
nn.ReLU(),
nn.Linear(num_units, 2),
]
)
self.step_embeddings = nn.ModuleList(
[
nn.Embedding(n_steps, num_units),
nn.Embedding(n_steps, num_units),
nn.Embedding(n_steps, num_units),
]
)
def forward(self, x_0, t):
x = x_0
for idx, embedding_layer in enumerate(self.step_embeddings):
t_embedding = embedding_layer(t)
x = self.linears[2 * idx](x)
x += t_embedding
x = self.linears[2 * idx + 1](x)
x = self.linears[-1](x)
return x
6. 编写损失函数
\[L_{simple}(\theta)=\left\|\epsilon-\epsilon_\theta(\sqrt{\bar\alpha_t}x_0+\sqrt{1-\bar\alpha_t}\epsilon, t)\right\|^2
\]
def diffusion_loss_fn(model, x_0, alphas_bar_sqrt, one_minus_alphas_bar_sqrt, n_steps):
"""
对任意时刻t进行损失计算
"""
batch_size = x_0.shape[0]
# 对batchsize内,覆盖不同的时间t
t = torch.randint(0, n_steps, size=(batch_size // 2,))
t = torch.cat([t, n_steps-1-t], dim=0) #[batch_size, 1]
t = t.unsqueeze(-1)
a = alphas_bar_sqrt[t]
am1 = one_minus_alphas_bar_sqrt[t]
e = torch.randn_like(x_0)
x = x_0 * a + e * am1
output = model(x, t.squeeze(-1))
return (e - output).square().mean()
7.逆向采样函数
p_sample对应公式如下
\[x_{t-1}=\frac{1}{\sqrt{\alpha_t}}\left[x_t-\frac{\beta_t}{\sqrt{1-\bar\alpha_t}}\epsilon_\theta(x_t,t)\right]+\sigma_t^2z, z\in\mathcal N(0,1)
\]
def p_sample_loop(model, shape, n_steps, betas, one_minus_alphas_bar_sqrt):
"""
从t->t-1, t-1->t-2
"""
cur_x = torch.randn(shape)
x_seq = [cur_x]
for i in reversed(range(n_steps)):
cur_x = p_sample(model, cur_x, i, betas, one_minus_alphas_bar_sqrt)
x_seq.append(cur_x)
return x_seq
def p_sample(model, x, t, betas, one_minus_alphas_bar_sqrt):
t = torch.tensor([t])
coeff = betas[t] / one_minus_alphas_bar_sqrt[t]
epos_theta = model(x, t)
mean = (1 / (alphas[t]).sqrt()) * (x - (coeff * epos_theta))
z = torch.randn_like(x)
sigma_t = betas[t].sqrt()
sample = mean + sigma_t * z
return (sample)
print( 'Training model. ..' )
batch_size = 128
dataloader = torch.utils.data.DataLoader(dataset, batch_size=batch_size, shuffle=True)
num_epoch = 4000
model = MLPDiffusion(num_steps)
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)
for t in range(num_epoch):
for idx, batch_x in enumerate(dataloader):
loss = diffusion_loss_fn(model, batch_x, alphas_bar_sqrt, one_minus_alphas_bar_sqrt, num_steps)
optimizer.zero_grad()
loss.backward()
torch.nn.utils.clip_grad_norm_(model.parameters(), 1.)
optimizer.step()
if (t % 500 == 0):
print(loss)
x_seq = p_sample_loop(model, dataset.shape, num_steps, betas, one_minus_alphas_bar_sqrt)
fig, axs = plt.subplots(1, 10, figsize=(28, 3))
for i in range(1, 11):
cur_x = x_seq[i * 10].detach()
axs[i-1].scatter(cur_x[:,0], cur_x[:,1],color='red',edgecolor='white')
axs[i-1].set_axis_off()
axs[i-1].set_title('$q(\mathbf{x}_{' + str(i*10) +'})$')
Training model. ..
tensor(0.5626, grad_fn=<MeanBackward0>)
tensor(0.3345, grad_fn=<MeanBackward0>)
tensor(0.2871, grad_fn=<MeanBackward0>)
tensor(0.5278, grad_fn=<MeanBackward0>)
tensor(0.3790, grad_fn=<MeanBackward0>)
tensor(0.3016, grad_fn=<MeanBackward0>)
tensor(0.6516, grad_fn=<MeanBackward0>)
tensor(0.5635, grad_fn=<MeanBackward0>)








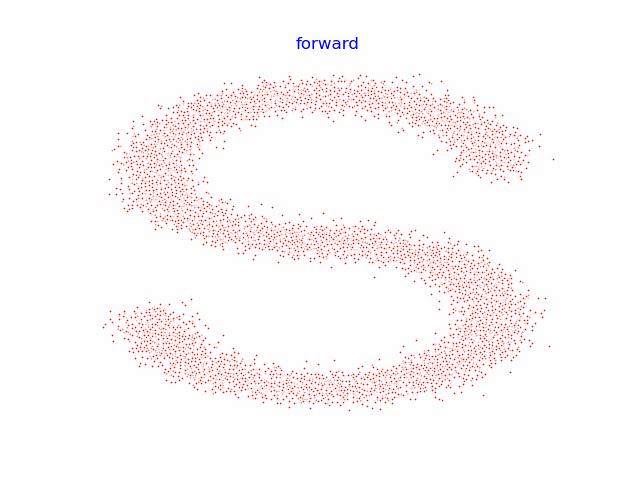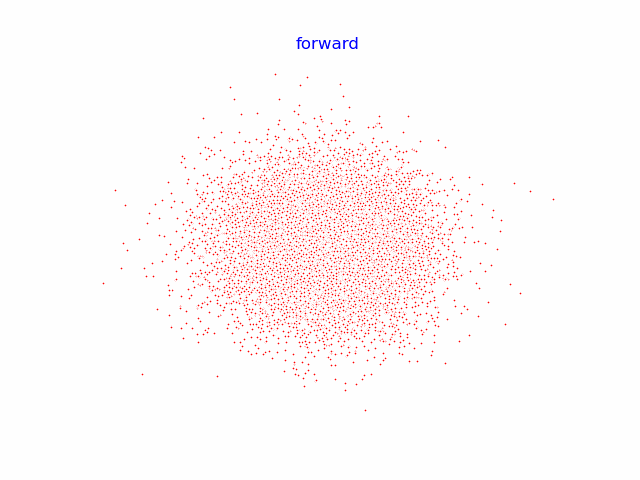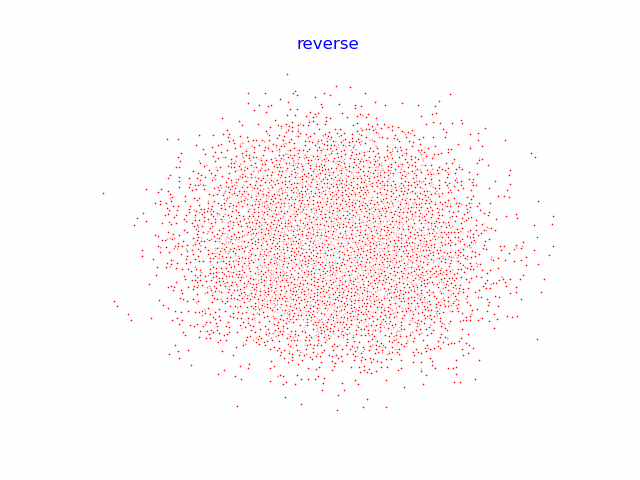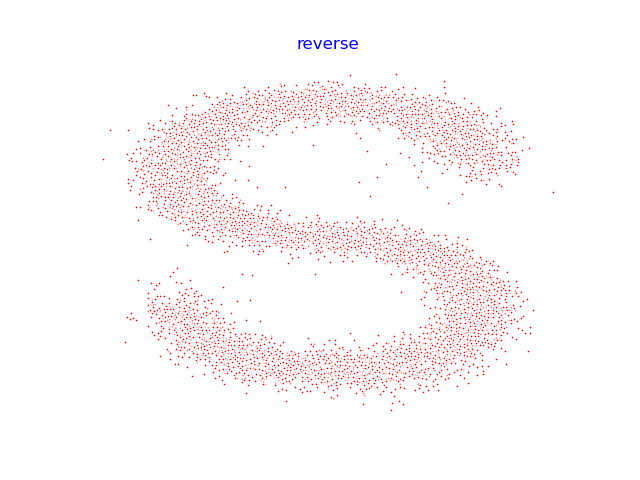
9.动画演示全过程
import io
from PIL import Image
imgs = []
for i in range(100):
plt.clf()
q_i = q_x(dataset, torch.tensor([i]))
plt.scatter(q_i[:,0], q_i[:,1], color='red', edgecolor='white', s=5)
plt.axis('off')
plt.title('forward')
img_buf = io.BytesIO()
plt.savefig(img_buf, format='png')
img = Image.open(img_buf)
imgs.append(img)
reverse = []
for i in range(100):
plt.clf()
cur_x = x_seq[i].detach()
plt.scatter(cur_x[:, 0], cur_x[:, 1], color='red', edgecolor='white', s=5)
plt.axis('off')
plt.title('reverse')
img_buf = io.BytesIO()
plt.savefig(img_buf, format='png')
img = Image.open(img_buf)
reverse.append(img)
imgs = imgs + reverse
imgs[0].save("diffusion.gif", format="GIF", append_images=imgs, save_all=True, duration=100, loop=0)




 浙公网安备 33010602011771号
浙公网安备 33010602011771号