ddpm扩散模型推导前置

扩散模型推导前置

鉴于扩散模型是一个非常严谨的数学推导过程，所以开始讲解DDPM等众多扩散模型公式前，需要先了解推导所需要的基本知识。其中涉及到的高等数学的内容都算比较简单的。本文将对论文的background段落的关键公式进行推导，尽量以高等数学基础知识解释清楚这里的背景原理，让看论文的人没那么懵逼。DDPM其实整个推导流程不复杂，也不难，如果有卡壳的地方不如放松脑子，往简单的方向想，不要想复杂了，想复杂了反而会对DDPM的原理很恐惧。

第一段

首先ddpm中正向过程\(0\rightarrow T\)的过程就是加噪声，从完整图片变成高斯噪声。从噪声生成图片就是逆向过程\(T\rightarrow 0\)。\(x_{0:T}\)的意思就是\(x_0,x_1,...,x_T\)的缩写，比如\(P(x_{0:T})=P(x_0,x_1,x_2,...,x_T)\)的联合概率分布。我们主要关注的就是逆向过程，也就是如何从高斯噪声生成一张图片。

第一个式子\(p_{\theta}(x_0):=\int p_{\theta}(x_{0:T})dx_{1:T}\)是概率论中联合分布的基本公式，即一个数据分布\(0\rightarrow T\)对\(1\rightarrow T\)做了积分以后，剩下的就是\(0\)处的概率分布，很好理解。\(p_\theta\)表示神经网络学习逆向过程，网络参数为\(\theta\)。逆向过程的起点\(x_T\)就是\(\mu=0,\sigma=1\)高斯噪声，表示为\(\mathcal N(x_T; 0,I)\)，\(x_T\)是我们提前定义好的高斯变量。与之相对的正向过程的数据分布由\(q\)表示，\(q\)并不需要使用网络学习。

第一段中还有一个重点就是，所有加噪声、去噪声的行为都定义为Markov chain(马尔科夫链)，意思就是只与前一项相关。比如在加噪声过程中\(x_3\)只和\(x_2\)相关，和\(x_1,x_0\)没有任何联系

第一个公式

我们来到了第一个公式中，附件(1)中有两个公式，左边的公式如下

\[p_\theta(x_{0:T}):=p(x_T)\prod_{t=1}^Tp_\theta(x_{t-1}|x_t) \]

我们可以通过这个公式知道\(p_\theta(x_{0:T})\)逆向过程的数据分布是如何计算的。右边的内容怎么来的，有一个非常简单的办法，ddpm所有的过程都是有限的\(T\)步，所以可以自己手写几项，整理完成后就可以推广到\(T\)项。以上述公式为例，我们手写一个\(p(x_1,x_2,x_3)\)为例子。根据概率论中的基本公式\(P(A,B)=P(A|B)P(B)=P(B|A)P(A)\)，易得

\[\begin{aligned} p(x_2, x_1, x_0) &= p(x_1, x_0 | x_2)p(x_2) &&(条件概率公式)\\ &=p(x_0|x_1,x_2)p(x_1|x_2)p(x_2) &&(条件概率公式的推广)\\ &=p(x_0|x_1)p(x_1|x_2)p(x_2) &&(马尔科夫链x_0只和x_1有关) \end{aligned} \]

在这个公式中，我们首先要意识到\(p\)代表逆向过程\(T\rightarrow 0\) ，所以下标大的作为概率条件计算下标小的概率，根据上述\(x_{0:2}\)的结果我们可以推广到\(x_{0:T}\)为如下结果

\[\begin{aligned} p(x_{0:T}) &= p(x_T,...,x_3,x_2,x_1,x_0) \\ &= p(x_0|x_1)p(x_1|x_2)p(x_2|x_3)...p(x_T) \\ &= p(x_T)\prod_{t=1}^Tp_\theta(x_{t-1}|x_t) \end{aligned} \]

由此我们得出了第一个公式的来源，接着我们看第二个公式如下：

\[p_\theta(x_{t-1}|x_t):=\mathcal N(x_{t-1};\mu_\theta(x_t,t),\Sigma_\theta(x_t,t)) \]

\(p_\theta\)用于训练逆向过程从高斯分布\(x_T\) 一步一步生成图像\(x_0\)，其中每一步都是通过神经网络训练的\((\mu_\theta,\Sigma_\theta)\)高斯分布得到

第二段

这一段的内容其实之前也提到了,\(q\)代表的是前向过程\(0 \rightarrow T\)，所以概率条件是小下标，概率分布是大下标。

前向过程同样是Markov chain，每一步根据方差\(\{\beta_1,...,\beta_T\}\)加入高斯噪声。\(\beta\)是啥目前还不用管，这是以后正文进行讲解的变量。

第二个公式

对于原文中的(2)目前也只看左边这个式子，即\(q\)加入噪声的数据分布计算公式：

\[q(x_{1:T}|x_0):=\prod_{t=1}^T q(x_t|x_{t-1}) \]

我们也可以写出具体的有限项的例子，然后推广到\(T\)，我们以\(q(x_{1:3}|x_0)\)为例子：

\[\begin{aligned} q(x_{1:3}|x_0) &= (x_3,x_2, x_1 | x_0) \\ &=q(x_3|x_2,x_1,x_0)q(x_2|x_1,x_0)q(x_1|x_0) &&(条件概率公式推广)\\ &=q(x_3|x_2)q(x_2|x_1)q(x_1|x_0) &&(马尔科夫链x_3只和x_2有关，x_2只和x_1有关) \end{aligned} \]

根据上面三项的结果，我们很容易就可以得到\(T\)项的表达式

\[q(x_{1:T}|x_0):=\prod_{t=1}^T q(x_t|x_{t-1}) \]

至此第二个公式也推导完毕

第三个公式

原文说公式(3)作为损失函数用于优化变分边界，同样我们先只看左半边的式子：

\[\mathbb E[-\log p_\theta(x_0)]\le\mathbb E_q\left[-\log\frac{p_\theta(x_{0:T})}{q(x_{1:T}|x_0)}\right] \]

首先，在第一段中已经告诉我们\(p_{\theta}(x_0):=\int p_{\theta}(x_{0:T})dx_{1:T}\)概率分布是这么计算的了，那么我们就从这个公式开始推导：

\[\begin{aligned} \mathbb E[-\log p_\theta(x_0)] &= -\log \int p_{\theta}(x_{0:T})dx_{1:T} \\ &= -\log\int q(x_{1:T}|x_0)\frac{p_{\theta}(x_{0:T})}{q(x_{1:T}|x_0)}dx_{1:T} &&(凑积分后面的x_{1:T},只有上一节推导的q能凑)\\ &=-\log \mathbb E_{q(x_{1:T}|x_0)}\left[\frac{p_{\theta}(x_{0:T})}{q(x_{1:T}|x_0)}\right] &&(期望的定义：\mathbb E_x(f(x)) = \int xf(x)dx) \end{aligned} \]

至此还差的区别在于我们推导出的结果\(\log\)在外面，而公式中的\(\log\)在期望里面，为此我们要引入Jessen不等式，对于上凸函数\(\log\)有以下性质:

\[\begin{aligned} f(\sum_{i=1}^M\lambda_ix_i) \ge\sum_{i=1}^M\lambda_if(x_i), &&\lambda_i\ge0 \end{aligned} \]

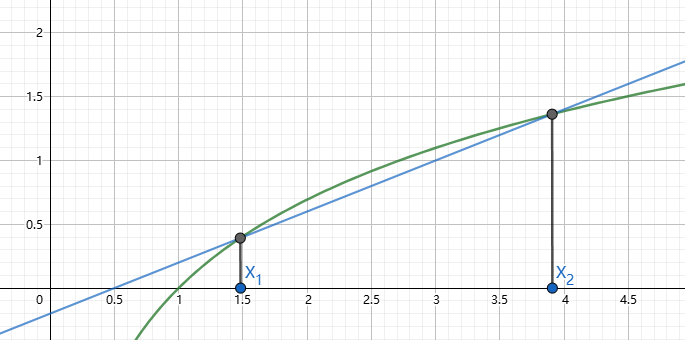
对于上凸函数，比如\(\log\)的Jessen不等式非常好理解，比如下图任取\(X_1,X_2\)为\(\log\)上的点连成直线，在区间\([X_1,X_2]\)之间我们可以看到直线永远小于等于\(\log\)函数，使用概率期望的表达如下公式表达如下：

\[f(\mathbb E(x)) \ge \mathbb E(f(x)) \]

我们将\(f(\cdot)\)使用\(\log\)函数套进去，额外的负号让不等式变号，则可以的得到：

\[\mathbb E[-\log p_\theta(x_0)] = -\log \mathbb E_{q(x_{1:T}|x_0)}\left[\frac{p_{\theta}(x_{0:T})}{q(x_{1:T}|x_0)}\right] \le \mathbb E_{q(x_{1:T}|x_0)}\log \left[\frac{p_{\theta}(x_{0:T})}{q(x_{1:T}|x_0)}\right] \]

至此我们完成了第三个公式的推导。

其他的前置知识

重采样技巧

若希望从高斯分布\(\mathcal N(\mu,\sigma)\)中采样，可以先从标准分布\(\mathcal N(0,1)\)采样出\(\epsilon\)，再得到\(\sigma \ast \epsilon+\mu\)，这样做的好处是将随机性转移到了常量\(\epsilon\)上。具体来说，我们要在如下高斯分布上采样：

\[p(x)=\mathcal N(\mu x_{t-1},\sigma^2) \]

我们的采样公式为如下公式，从一个标准正态分布中采样出我们需要的正态分布：

\[\begin{aligned} x=\mu x_{t-1}+\sigma\epsilon, && \epsilon\in\mathcal N(0,I) \end{aligned} \]

正太分布的性质

为了防止已经完全遗忘了概率论的知识，我们将一些用到的知识点重新罗列在这一小节。在正文中有看不懂的地方可以来这里查询。

\(X\sim \mathcal N(\mu, \sigma^2I)\)表示正态分布，其中\(\mu\)是均值，\(\sigma^2\)为方差，正态分布的计算公式如下：

\[p(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(x-\mu)^2}{2\sigma^2}) \]

假设\(X_1\sim \mathcal N(\mu_1, \sigma_1^2I)\),\(X_2\sim \mathcal N(\mu_2, \sigma_2^2I)\),则\(X_1+X_2 \sim \mathcal N(\mu_1+\mu_2, (\sigma_1^2+\sigma_2^2)I)\)

KL散度

KL散度用于衡量两种分布的相似性公式表示如下：

\[D_{KL}(p(x)\|q(x)) =\int p(x)\log\frac{p(x)}{q(x)}dx \]

KL散度越小代表越接近，KL散度越大越不同。

高斯分布的KL散度

对于两个单一变量的高斯分布\(p(x)\)和\(q(x)\)，他们的KL散度如下：

\[D_{KL}(p(x)\|q(x)) = \log \frac{\sigma_q}{\sigma_p} + \frac{\sigma_p^2+(\mu_p-\mu_q)^2}{2\sigma_q^2}-\frac{1}{2} \]

推导过程如下，假设高斯分布为\(p(x)=\mathcal N(\mu_p,\sigma_p^2),q(x)=\mathcal N(\mu_q,\sigma_q^2)\),带入上一小节KL散度公式中的\(\log \frac{p(x)}{q(x)}\)：

\[\begin{aligned} \log\frac{p(x)}{q(x)} &= \log \frac{\frac{1}{\sqrt{2\pi}\sigma_p}\exp(-\frac{(x-\mu_p)^2}{2\sigma_p^2})}{\frac{1}{\sqrt{2\pi}\sigma_q}\exp(-\frac{(x-\mu_q)^2}{2\sigma^2_q})} \\ &=\log\left[ \frac{\sigma_q}{\sigma_p}\exp(-\frac{(x-\mu_p)^2}{2\sigma_p^2}+\frac{(x-\mu_q)^2}{2\sigma_q^2}) \right] \\ &=\log\frac{\sigma_q}{\sigma_p} + \frac{(x-\mu_q)^2}{2\sigma_q^2}-\frac{(x-\mu_p)^2}{2\sigma_p^2} \end{aligned} \]

则KL散度

\[\begin{aligned} D_{KL}(p(x)\|q(x)) &= \int p(x)\left[ \log\frac{\sigma_q}{\sigma_p} + \frac{(x-\mu_q)^2}{2\sigma_q^2}-\frac{(x-\mu_p)^2}{2\sigma_p^2}\right]dx \\ &=\int p(x) \log\frac{\sigma_q}{\sigma_p}dx &(I_1)\\ &+ \frac{1}{2\sigma_q^2}\int p(x)(x-\mu_q)^2dx &(I_2) \\ &-\frac{1}{2\sigma_p^2}\int p(x)(x-\mu_p)^2dx &(I_3) \end{aligned} \]

计算\(I_1\)

\[\begin{aligned} I_1&=\int p(x) \log\frac{\sigma_q}{\sigma_p}dx \\ &=\log\frac{\sigma_q}{\sigma_p} \int p(x)dx &(正态分布积分为1)\\ &=\log \frac{\sigma_q}{\sigma_p} \end{aligned} \]

计算\(I_2\)

\[\begin{aligned} I_2 &= \frac{1}{2\sigma_q^2}\int p(x)(x-\mu_q)^2dx \\ & =\frac{1}{2\sigma_q^2}\int p(x)(x-\mu_p+\mu_p-\mu_q)^2dx&(构造) \\ &= \frac{1}{2\sigma_q^2}\int p(x)\left[(x-\mu_p)^2+2(x-\mu_p)(\mu_p-\mu_q) + (\mu_p-\mu_q)^2\right]dx \\ &= \frac{1}{2\sigma_q^2}\left[\int p(x)(x-\mu_p)^2dx + 2(\mu_p-\mu_q)\int p(x)(x-\mu_p)dx+(\mu_p-\mu_q)^2\int p(x)dx \right] \end{aligned} \]

第一项根据高斯分布方差的定义\(\int p(x)(x-\mu_p)^2dx=\sigma_p^2\)。

第二项根据高斯分布的中心对称性\(\int p(x)(x-\mu_p)dx=0\)

\(p(x)\)高斯分布是\(y\)轴对称的偶函数，\(x-\mu_p\)是过原点的奇函数，所以\(p(x)(x-\mu_p)\)是奇函数，所以积分为0

第三项根据高斯分布的定义\(\int p(x)dx=1\)

综上

\[I_2=\frac{1}{2\sigma_q^2}[\sigma_p^2+(\mu_p-\mu_q)^2] \]

计算\(I_3\)

\[I_3 = \frac{1}{2\sigma_p^2}\int p(x)(x-\mu_p)^2dx =\frac{1}{2\sigma_p^2}\cdot\sigma_p^2=\frac{1}{2} \]

合并结果

将\(I_1,I_2,I_3\)合并：

\[D_{KL}(p\|q) =\log \frac{\sigma_q}{\sigma_p}+\frac{1}{2\sigma_q^2}[\sigma_p^2+(\mu_p-\mu_q)^2]-\frac{1}{2} \]

附件（原文background）