时空复杂度分析

算法的复杂度是评估算法优劣一个重要指标，可以帮助我们估算出算法在执行之后所需要的时间和空间。算法的复杂度分为算法的时间复杂度和空间复杂度。在介绍时间复杂度之前，我们需要引入时间频度的概念。时间频度是指算法中语句的执行次数，用\(T(n)\)来表示，\(n\)为问题的规模。

在算法竞赛中，一般为了理解方便，只用\(O(n)\)表示复杂度。简单来说，用时间频度的表达方法不够简洁，于是引入了时间复杂度的概念。如果有一个辅助函数\(f(n)\)，在\(n\)趋向于无穷大时，\(T(n) \div f(n)\)的极限值为不等于0的常数，则我们近似的将\(f(n)\)替代\(T(n)\)，记为\(T(n) = O(f(n))\)，称为算法的渐进时间复杂度。

时间复杂度只需要计算算法中最耗时的部分，舍去常数部分，通常用简单的函数来表示。例如，某算法时间频度\(T(n)=2n^3+4n^2+n\)，则它的时间复杂度为\(O(n^3)\)。按效率从高到低排列，时间复杂度一般有以下几种：

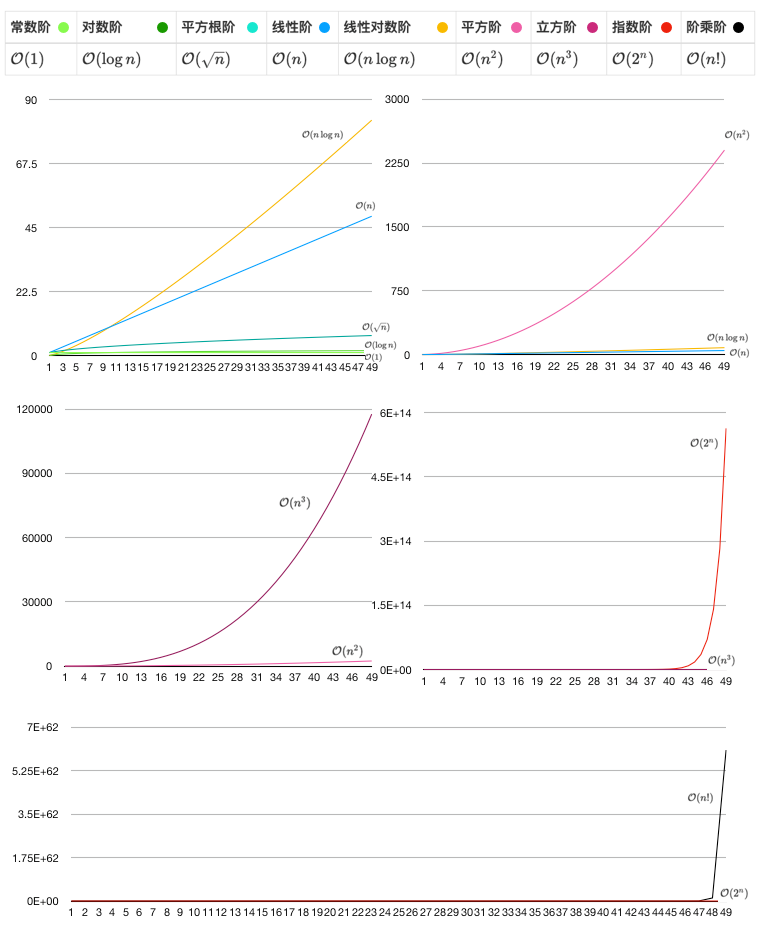
我们举个例子来描述下算法时间复杂度的计算过程。现有如下代码，可以计算出语句1执行了\(n^2\)次，语句2执行了\(n\)次，语句3执行了\(log(n)\)次，则\(T(n)=n^2+n+log(n)\)，取最耗时部分计算，则时间复杂度为\(O(n^2)\)。

for (int i = 0; i < n; ++i) {
    for (int j = 0; j < n; ++j) {
        a++; //  语句 1
    }
}
for (int i = 0; i < n; ++i) {
    b++; //语句 2
}
while (n) {
    n = n / 2; //语句 3
}

算法的空间复杂度是指运行该算法所占用的存储空间大小，记为\(S(n)\)。和时间复杂度类似，通常也是取它的渐进空间复杂度，用一个直观的函数来表示。通过空间复杂度，我们可以预估出算法运行所需的存储空间，包括指令空间、数据空间、动态申请的内存空间等。

有如下代码，可以计算出\(S(n)=N^2+n\)，则空间复杂度为\(O(n^2)\)。

int a[n];
int b[n][n];

在使用函数递归的时候，别忘记递归消耗的栈空间。

在竞赛中，我们一般认为计算机一秒能执行\(5\times10^8\)如果题目给出的时间限制为\(1\)秒，那么你选择的算法执行的计算次数最多应该只能在\(10^8\)量级解决这个题目。

一般地：

\(O(n)\)的算法能解决的数据范围在\(n\le10^8\)

\(O(nlog(n))\)的算法能解决的数据范围在\(n\le10^6\)

\(O(n\sqrt n)\)的算法能解决的数据范围在\(n\le10^5\)

\(O(n^2)\)的算法能解决的数据范围在\(n\le5000\)

\(O(n^3)\)的算法能解决的数据范围在\(n\le300\)

\(O(2^n)\)​​​​的算法能解决的数据范围在\(n\le25\)

\(O(n!)\)的算法能解决的数据范围在\(n\le11\)

以上范围仅供参考，实际中还需要考虑每种算法的常数。