各种排序(二)
- 本文中 \(n\) 代表着待排序序列的长度。
- 算法是否稳定:若 \(a_i = a_j \ , \ i < j\),排序后若\(i < j\) 则稳定,反之不稳定。(可能有点歧义凑活看)
归并排序
用了二分的思想。
在递归的过程中不断将需要排序的区间缩小,使小区间有序后,再使大区间变得有序会简单很多。
最差时间复杂度:\(O(nlogn)\)
最优时间复杂度:\(O(nlogn)\)
平均时间复杂度:\(O(nlogn)\)
算法是否稳定:是
void mergesort(int l,int r,int mid) {//将[l,r]区间排好序
int i=l,j=mid+1,cnt=0;//[l,mid]与[mid+1,r]已经有序了,所以可以进行下面的操作。
while(i<=mid&&j<=r) temp[++cnt]=a[i]<=a[j]?a[i++]:a[j++];
while(i<=mid) temp[++cnt]=a[i++];
while(j<=r) temp[++cnt]=a[j++];
for(int i=l;i<=r;++i) a[i]=temp[i-l+1];
}
void merge(int l,int r) {//不断将区间缩小
if(l==r) return;
int mid=(l+r)>>1;
merge(l,mid),merge(mid+1,r);
mergesort(l,r,mid);return;//递归,先给小区间排序后大区间。
}
merge(1,n);
上张图理解一下: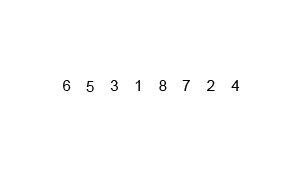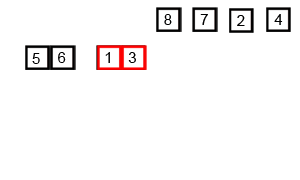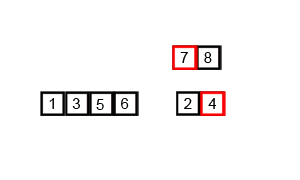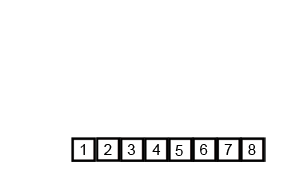
可用于求逆序对的个数。
堆排序
不想写,咕咕咕。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号