2个2D向量计算交点的夹角和补角

2维向量如何计算与某一个交点之间的夹角,假设A,B是向量,C是他们共同连接的一个点计算出A-C-B形成的角度

 

我们先了解几个简单的计算:

2D向量的乘积计算	(A.x * B.x + A.y * B.y)
2D向量的取摸	开平方(A.x * A.x + A.y * A.y)
弧度转换角度	弧度 除以 圆周率 再乘以180
角度转换弧度	角度 乘以 圆周率 后再除以180
补角	计算方式1:  补角 = 180 - 正角. 计算方式1:  两个向量方向一正一反就可以计算出补角

如果你理解了以上公式,那么来看看如何计算夹角的公式,两向量夹角余弦等于向量数量积除以两向量模的乘积

公式1： cos角度=(ac+bd)/( 根号(a*a+b*b) ) * ( 根号(c*c+d*d))

推导1： 弧度= 反cos((ac+bd)/(根号a*a+b*b) * (根号(c*c+d*d)))

推导2： 角度= 反cos((ac+bd)/(根号a*a+b*b) * (根号(c*c+d*d))) / 圆周率 * 180;

 

公式代码实现：

public void JiSun() 
    {
        hudu = Math.Acos(
             (ac.x * cb.x
            + ac.y * cb.y)
            / (Mathf.Sqrt(ac.x * ac.x + ac.y * ac.y)
            * Mathf.Sqrt(cb.x * cb.x + cb.y * cb.y)));

        //弧度转换角度
        jiajiao = hudu / Math.PI * 180;
        补角.text = jiajiao + "度";
    }

 

项目源码：http://yunpan.cn/cdrmEcDjfSDMD  访问密码 d262

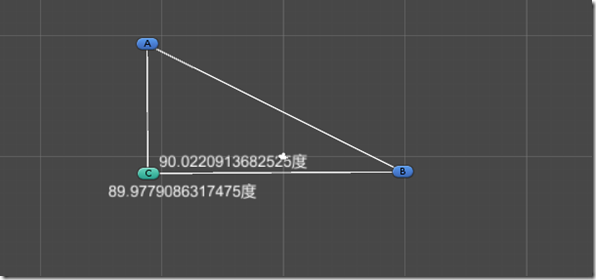
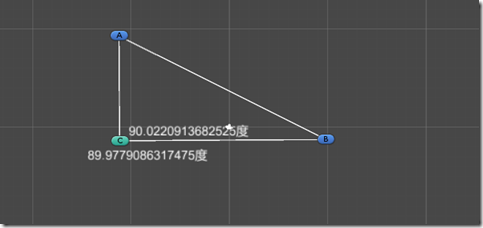
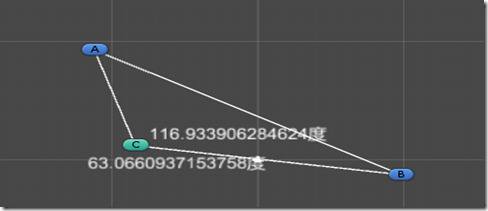
效果图:

 

工程代码：

using UnityEngine;
using System.Collections;
using UnityEditor;
using System;

public class Test : MonoBehaviour {


    public Transform a;
    public Transform b;
    public Transform c;
    public TextMesh 正角;
    public TextMesh 补角;

    // Update is called once per frame
    void Update () {

        Vector3 ac = a.position - c.position;
        Vector3 bc = b.position - c.position;
        Vector3 cb = c.position - b.position;


        /*
         * cos＜A,B＞=(ac+bd)/(根号a*a+b*b)(根号c*c+d*d)
         * 两向量夹角余弦等于向量数量积除以两向量模的乘积 
         */
        double hudu = Math.Acos(
                             (ac.x * bc.x
                            + ac.y * bc.y)
                            / (Mathf.Sqrt(ac.x * ac.x + ac.y * ac.y)
                            * Mathf.Sqrt(bc.x * bc.x + bc.y * bc.y)));
        //弧度转换角度
        double jiajiao = hudu / Math.PI * 180;


        正角.text = jiajiao + "度";
        //补角.text = (180 - jiajiao) + "度";



        hudu = Math.Acos(
                     (ac.x * cb.x
                    + ac.y * cb.y)
                    / (Mathf.Sqrt(ac.x * ac.x + ac.y * ac.y)
                    * Mathf.Sqrt(cb.x * cb.x + cb.y * cb.y)));

        //弧度转换角度
        jiajiao = hudu / Math.PI * 180;
        补角.text = jiajiao + "度";

    }

    //绘制线段
    public void OnDrawGizmos() 
    {
        Gizmos.DrawLine(a.position, b.position);
        Gizmos.DrawLine(a.position, c.position);
        Gizmos.DrawLine(b.position, c.position);
    }

    //以原点计算两个坐标的夹角
    public void OriginAngle() 
    {
        double hudu = Math.Acos(
                     (a.position.x * b.position.x
                    + a.position.y * b.position.y)
                    / (Mathf.Sqrt(a.position.x * a.position.x + a.position.y * a.position.y)
                    * Mathf.Sqrt(b.position.x * b.position.x + b.position.y * b.position.y)));

        double jiajiao = hudu / Math.PI * 180;
        正角.text = jiajiao + "度";
    }

}