人工智能基础笔记 · Part B 人工神经网络

C3 人工神经网络

ANN，Artificial Neural Networks。属于连接主义的范畴。

本质上是在形成图。有/无环、有/无向图。

从 1943 年的模型出发

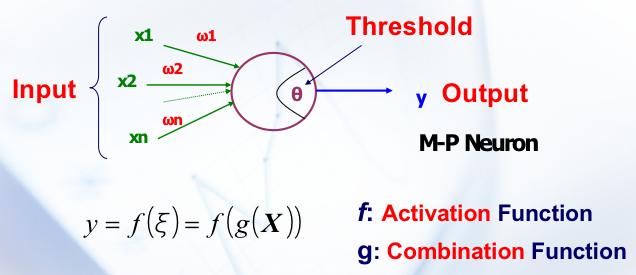
接受输入 \(X\)，给出输出 \(y\)。通过 \(g(X)\) 对 \(x_1,x_2,x_3\) 来组合，看组合结果的是否超过一个阈值，返回一个 \(y=f(g(X))\) ，这个 \(f\) 就可以看做是在和阈值作比较并决定最后输出什么。

\(g\) 的选择

• Weighted Sum

\[\begin{aligned} \xi & =g(\boldsymbol{X})=\sum_{i=1}^n \omega_i x_i-\theta \\ y & =f(\xi)=f\left(\sum_{i=1}^n \omega_i x_i-\theta\right) \longrightarrow y=f(\xi)=f\left(\sum_{i=0}^n \omega_i x_i\right) \end{aligned} \]

• Radial Distance

\[\xi=\|\boldsymbol{X}-\boldsymbol{C}\|=\sqrt{\sum_{i=1}^n\left(x_i-c_i\right)^2} \quad y=f(\xi)=f\left(\sqrt{\sum_{i=1}^n\left(x_i-c\right)^2}\right) \]

\(f\) 的选择

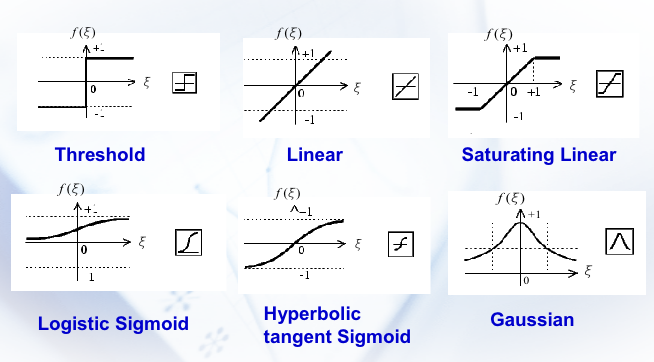
一些比较厉害的激活函数 \(f\)。

现在面临的问题有两个：

• 如何连接各个单元？

• 如何自动调整 ANN 中边的权值甚至是结构？

神经网络

接下来是把神经元连起来的工作。

前向神经网络 Feedforward networks

反馈神经网络 Feedforward networks

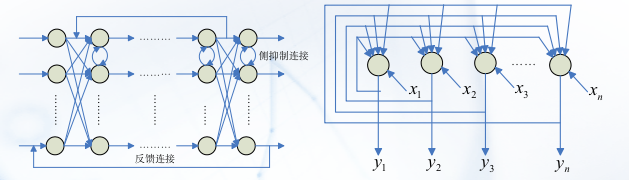
神经网络的训练，就是神经网络的自由参数（例如权重和偏差）通过与其所处环境相互作用而得到调整的过程。

不同的学习策略

错误修正 Error Correction

监督学习。通常的表达是 \(\omega \leftarrow \omega+\Delta \omega=\omega+\eta \delta\) 。

赫布学习 Hebbian Learning

无监督学习。基本的思想是 “在神经网络中，如果一个神经元的活动频率与另一个神经元的活动频率高度相关，那么它们之间的连接强度应该增加”。

\(\omega_{i j}(t+1)=\omega_{i j}(t)+\eta\left(x_i(t) \cdot x_j(t)\right)\)

竞争学习 Competitive Learning

无监督学习。赢者通吃的思想。Winner-take-all, WTA。在这种机制中，网络中的神经元相互竞争以对输入信号做出响应，最终只有一个或少数几个神经元被激活。这种方法主要用于模式识别和决策制定过程。换言之：发掘特征。

• 硬竞争（Hard competition）

对于给定的输入，只有一个神经元被激活。这意味着网络作出了一个非常明确的选择，只有一个“赢家”。这是一种更为严格和排他性的响应模式。

• 软竞争（Soft competition）

软竞争允许除了最强信号的神经元外，其邻近的神经元也部分激活。这种方法提供了更多的灵活性和鲁棒性，因为它允许网络识别和响应类似但不完全相同的模式。

多层感知机 MLP

单层感知机 （1957）

大概长这样：

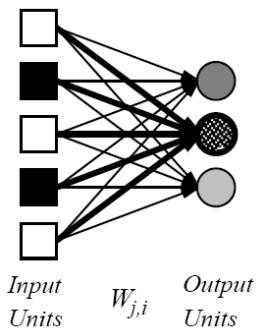
可以通过简单的方式来调整参数：

\[\omega_{ij} \leftarrow \omega_{ij} + \eta \cdot x_i \cdot (d_j - y_j), \quad y_j = f\left(\sum_{i=0}^{m} \omega_{ij} \cdot x_i\right) \]

其中用到了预期输出和真实输出的差值。

一个比较有意思的点是，单层感知机可以表达与运算、或运算和非运算，但不能表达异或运算（线性不可分）。

• 与运算

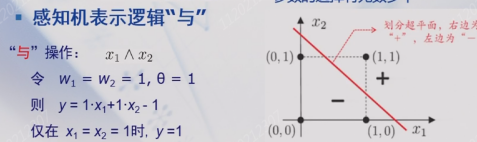
• 或运算

• 非运算

事实上，3 layers 即可以表示 All continuous functions，4 layers 就可以表示 all functions。

深度学习

Deep architectures are composed of multiple levels (usually >3) of non-linear operations, such as neural nets with many hidden layers.

层数越高，抽象程度越高。某些功能无法通过太浅的架构有效地表示（就可调元素的数量而言），深层架构也许能够表示一些原本无法有效表示的功能。

发展缓慢的原因：

• 梯度扩散，传递到底层时影响很少了。

• 缺少带标签的数据，也即缺少数据集。

深度神经网络主要采取这样的思路：

–Sigmoid nonlinearity for hidden layers.

–Softmax for the output layer.

B-P Network

Back-Propagation (B-P) Algorithm and Network。一种结构上最简单的有趣 MLP。具体的算法如下：

• 输入数据从输入层传递到隐藏层，然后传递到输出层（前向传播）。

• 错误信息从外层向后传播到隐藏层，然后传播到输入层（反向传播）。

具体而言， \(\bold w\cdot \bold x + b = \sigma_j'\) ，经过激活函数变成了隐藏层保留的值 \(y_j'\)，接着 \(y_j'\) 隐藏层再经过一次线性组合得到 \(\sigma _i\)，经过激活函数变成了输出 \(y_i\)。所以过程是线性组合 \(\to\) 激活函数 \(\to\) 线性组合 \(\to\) 激活函数。也即，通常在隐藏层和输出层的线性组合之后都会有激活函数的步骤。

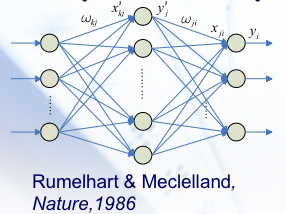
简单步骤

• 从训练集中选择一个模式并将其呈现给网络。

• 计算该序列中输入、隐藏和输出神经元的激活值（每个节点的输出）。

• 通过将生成的输出与所需的输出进行比较来计算输出神经元的误差。

• 使用计算出的误差来更新网络中的所有权重，从而减少全局误差测量。

• 重复步骤 1 到步骤 4，直到全局误差低于预定义的阈值。

误差的衡量。采用平方损失（Mean Squared Error，MSE）。

进而可以使用梯度下降法调整参数：

\[\begin{gathered} \boldsymbol{\omega}=\boldsymbol{\omega}+\eta \underbrace{[-\nabla e(\boldsymbol{\omega})]}_\delta \\ \omega=\omega-\eta \frac{\partial e}{\partial \omega} \end{gathered} \]

右侧连边 \(\omega_{j i}\)

那么对于隐藏层和输出层 \(Y\)：

\[\begin{gathered} \omega_{j i}=\omega_{j i}-\eta x_{j i} y_i\left(1-y_i\right)\left(y_i-d_i\right) \\ \frac{\partial e}{\partial \omega_{j i}}=\frac{\partial e}{\partial y_i} \frac{\partial y_i}{\partial \sigma_i} \frac{\partial \sigma_i}{\partial \omega_{j i}} \end{gathered} \]

计算过程如下：

\[\left.\begin{array}{l} e=\frac{1}{2} \sum\left(d_i-y_i\right)^2 \Rightarrow \frac{\partial e}{\partial y_i}=\left(y_i-d_i\right) \\ y_i=\frac{1}{1+e^{-\sigma_i}} \Rightarrow \frac{\partial y_i}{\partial \sigma_i}=y_i\left(1-y_i\right) \\ \sigma_i=\sum \omega_{j i} x_{j i} \Rightarrow \frac{\partial \sigma_i}{\partial \omega_{j i}}=x_{j i} \end{array}\right\}-\frac{\partial e}{\partial \omega_{j i}}=x_{j i} y_i\left(1-y_i\right)\left(y_i-d_i\right) \]

这个地方的激活函数选择了 sigmoid 作为激活函数的原因是它导数的形态很合理，且范围合理：

\[\sigma^{\prime}(x)=\sigma(x) \cdot(1-\sigma(x)) \]

左侧连边 \(\omega_{kj}\)

\[\frac{\partial e}{\partial \omega_{k j}}=\sum_{i=1}^n \frac{\partial e}{\partial y_i} \frac{\partial y_i}{\partial \sigma} \frac{\partial \sigma}{\partial y_j^{\prime}} \frac{\partial y_j^{\prime}}{\partial \sigma^{\prime}} \frac{\partial \sigma_j^{\prime}}{\partial \omega_{k j}} \]

总之就是算来算去，可以得到最终的形式如下：

\[\begin{gathered} \frac{\partial e}{\partial y_i}=\left(y_i-d_i\right), \frac{\partial y_i}{\partial \sigma_i}=y_i\left(1-y_i\right), \frac{\partial \sigma_i}{\partial y_j^{\prime}}=\omega_{j i}, \frac{\partial y_j^{\prime}}{\partial \sigma_j^{\prime}}=y_j^{\prime}\left(1-y_j^{\prime}\right), \frac{\partial \sigma_j^{\prime}}{\partial \omega_{k j}}=x_{k j} \\ \frac{\partial e}{\partial \omega_{k j}}=x_{k j} y_j^{\prime}\left(1-y_j^{\prime}\right) \sum_{i=1}^n\left[\omega_{j i} y_i\left(1-y_i\right)\left(y_i-d_i\right)\right] \\ \Longrightarrow \omega_{k j}=\omega_{k j}-\eta x_{k j} y_j^{\prime}\left(1-y_j^{\prime}\right) \sum_{i=1}^n \omega_{j i} y_i\left(1-y_i\right)\left(y_i-d_i\right) \end{gathered} \]

深度信念网络 DBNs

Deep Belief Networks。这块真看不懂。所以只能大概理解一下结构了：

受限玻尔兹曼机 RBM

Restricted Boltzmann Machines，一个两层结构的网络。RBM 是一种无监督的能量基模型，其核心思想是通过一个能量函数来定义网络的状态。

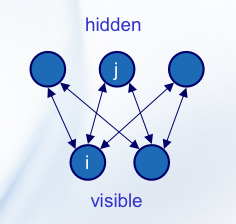
• 可见层（Visible Layer）：代表观察到的数据，可以是任何类型的输入数据，比如图片的像素值、文本的词向量等。

• 隐藏层（Hidden Layer）：代表数据的特征，这些特征是模型通过学习数据分布自动捕捉到的。

RBM 的特点在于其层内的节点不相互连接，只有可见层与隐藏层之间存在连接，这些连接是双向的并且权重是对称的。这种结构限制了网络的复杂性，同时使得训练算法（如对比散度，Contrastive Divergence, CD）能够有效地更新权重。

RBM 中的每一个状态（即可见层和隐藏层的神经元配置）都有一个定义好的能量，该能量由网络的权重和偏置确定，对于给定的可见单元的状态 $\mathbf{v} $ 和隐藏单元的状态 $\mathbf{h} $，RBM的能量函数 $E $ 定义为：

\[E(\mathbf{v}, \mathbf{h}) = -\sum_{i} a_i v_i - \sum_{j} b_j h_j - \sum_{i,j} v_i w_{ij} h_j \]

其中：

• $a_i $ 是可见单元 $v_i $ 的偏置。
• $b_j $ 是隐藏单元 $h_j $ 的偏置。
• $w_{ij} $ 是可见单元 $i $ 和隐藏单元 $j $ 之间的权重。

那么 RBM 中可见单元和隐藏单元的联合概率分布由下面的玻尔兹曼分布给出：

\[P(\mathbf{v}, \mathbf{h}) = \frac{1}{Z} e^{-E(\mathbf{v}, \mathbf{h})} \]

这里 $Z $ 是配分函数（归一化常数），定义为所有可能状态的能量的指数和的总和。但这个通常没法算。

真正需要的是可见单元的边缘概率分布，但实际应用中直接计算边缘分布不可行，因此通常使用一些近似方法，如对比散度（Contrastive Divergence, CD）算法，来近似地学习模型参数。通过这样的训练过程，RBM 能够学习到一个近似的数据分布，使得通过该分布生成的数据和真实数据尽可能相似。

DBNs 结构

DBNs 的结构可以如此刻画：显层（输入层）\(\to\) 隐层 \(\to\) 隐层 \(...~ \to\) 隐层 \(\to\) 输出层。其中，中间的层均为 RBM，最后一个隐层和输出层之间是 BP。因此，DBNs 可以认为是由多层受限玻尔兹曼机堆叠而成，每一层都对上一层的表示进行进一步抽象。采用无监督预训练，逐层构建复杂模型。

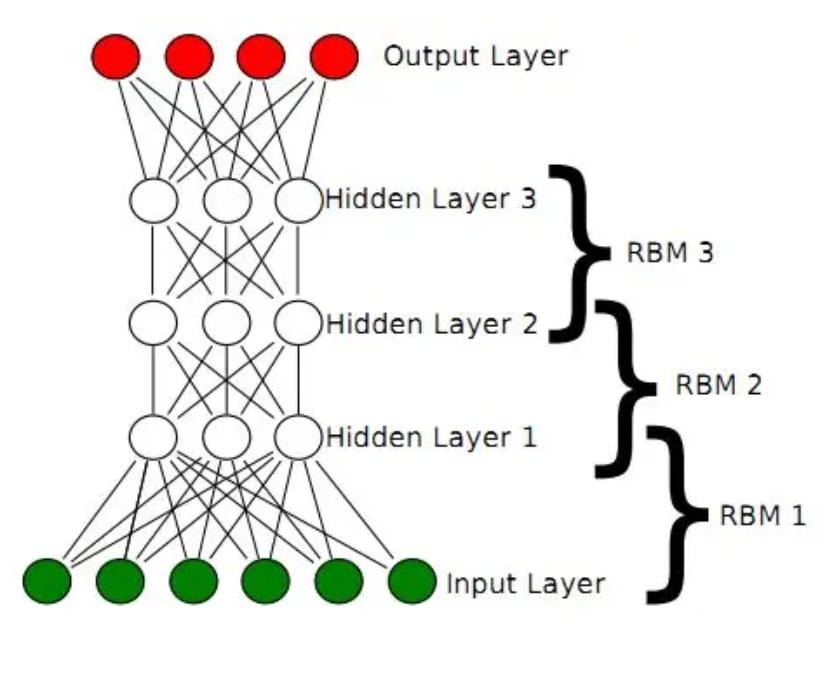
算法步骤如下：

• 前向传播: 从可见层到隐藏层的激活。

• 后向传播: 从隐藏层到可见层的重构。

• 梯度计算: 通过对比散度( Contrastive Divergence,CD ) 计算权重更新的梯度。

• 权重更新: 通过学习率更新权重。

其训练过程可以分为两个阶段：

• 预训练阶段: 每个 RBM 层按照从底到顶的顺序进行贪心逐层训练。

• 微调阶段(fine-tuning): 使用监督学习方法( 如反向传播)对整个网络进行微调。

RBM 层能贪心的原因是，我们可以通过无监督学习使得 RBM 的能量值来到最小，此时每个 RBM 层可以独立地学习到一个对输入数据有效的表示。那之后微调自然是和 B-P 一样的思路，要选择一个最佳的表示。

AutoEncoder

一种前馈神经网络结构，由编码器（encoder）和解码器（decoder）组成，用于学习输入数据的紧凑表示。往往通过监督学习或无监督学习进行训练，目标是最小化输入和重构输出之间的差异。主要用于数据压缩、去噪、特征学习等任务。

为啥这块知识会出现在这里，我毫无头绪。

Hopfield Neural Network 霍普菲尔德网络

基本逻辑

1982。属于 Feedback Networks，也叫做 Recurrent Neural Network，循环神经网络。对于循环神经网络，通常追求其能达到某个稳定的状态，即 \(Y(t) = Y(t + 1)\) 。

冥思苦想半天终于明白是怎么个事儿了。HNN 的意思是，一开始给出了 \(K\) 组输入/训练集作为初始模式/吸引子，通过这些输入获得了一组权重 \(w\)。那么再让新的输入进来的时候，他就会自动朝着最相近的 \(K\) 组输入之一靠拢，来实现一个分类器的作用，其中分类的基准是这些预先“记忆”的吸引子。下面是个不错的例子。左侧是初始模式，右侧是四个输入，他们分别最后被联想成了 \(3\)，其实就是分类进了 \(3\)。

所以，Hopfield 网络常常可以用于联想记忆，因此又称联想记忆网络。与人脑的联想记忆功能类似，Hopfield 网络实现联想记忆需要两个阶段：

• 记忆阶段

在记忆阶段，外界输入的数据使得系统自动调整网络的权值，最终用合适的权值使系统具有若干个稳定状态，即吸引子(attractor)。其吸引域半径定义为吸引子所能吸引的状态的最大距离。吸引域半径越大，说明联想能力越强。联想记忆网络的记忆容量定义为吸引子的数量。

• 联想阶段

在联想阶段，对于给定的输入模式，系统经过一定的演化过程，最终稳定收敛于某个吸引子。

结构特点

此处 HNN 专指 DHNN（离散的，神经元 \(= +1/-1\)）。

• 只有单层。虽然这个地方定义层有点诡异。

• 每个神经元可以处于激活（通常表示为 \(+1\)）或未激活（表示为 \(-1\)）的状态。神经元节点之间是全连接的，且权重对称。

• 只有输入，没有输出。

• 可以到达稳定状态。

权重和势能函数

势能函数 \(E\)。取自热力学概念，当 \(E\) 最小时，系统进入稳定。对于当前的联想分类问题，则是会让数据进入到某个吸引子状态。具体可以让参考下图：

Hopfield 证明了当权重满足下述条件时，\(E\) 一定会来到极小值处：

\[w_{i j}=\left\{\begin{array}{l} w_{j i}, i \neq j \\ 0, i=j \end{array}\right. \]

因此假设我们预先准备了 \(K\) 组吸引子 \(X_1~X_K\)，这些吸引子的长度为 \(n\)，那么可以通过这种方式得到一组符合要求的权重（两种表述）：

\[\begin{aligned} & \boldsymbol{\omega}=\sum_{k=1}^K \boldsymbol{X}_k \boldsymbol{X}_k^T-K \boldsymbol{I} \\ & \omega_{i j}=\left\{\begin{array}{l} \sum_{k=1}^K x_{i k} x_{j k}, i \neq j \\ 0, i=j \end{array}\right. \end{aligned} \]

进一步，势能函数可以如此定义。

• With input

\[E=-\frac{1}{2} \sum_{i=0}^n \sum_{j=0}^n \omega_{i j} s_i s_j-\sum_{i=1}^n I_i s_i \]

• Without input

\[E=-\frac{1}{2} \sum_{i=0}^n \sum_{j=0}^n \omega_{i j} s_i s_j=-\frac{1}{2} \boldsymbol{S}^T \boldsymbol{\omega} \boldsymbol{S} \]

其中，\(s_i\) 表示的是第 \(i\) 个神经元的状态。\(I_i\) 表示的则是输入的第 \(i\) 项。值得一提的是，权重矩阵 \(w\) 的边长 = 外部输入向量 \(I\) 的长度 = 初始设置的吸引子的边长。举个例子来说，就是把鸭子分类成鸭子，那这两个鸭子需要是同一个形态的。很神奇的一个构造是，神经元的数量恰好等于吸引子的长度。

以下是一个例子：

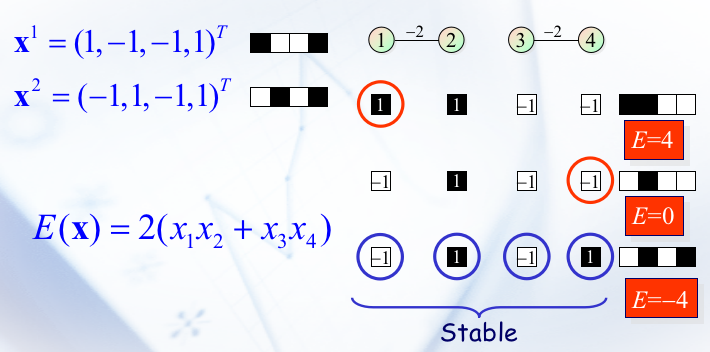
而关于怎么走到一个稳定状态，似乎是看脸？ 我本来以为真的是瞎选的，结果 G4 老师说：

这一步 \(S \to h\) 的过程就是一个时序的过程。更新神经元 \(i\) 的状态时，确实是在计算从时间 \(t\) 到 \(t+1\) 的转变。另外，每个神经元的状态更新只由其他神经元的状态决定，而不是由它自身的当前状态直接决定。具体原因还是看 G 老师吧：

DHNN 解决 TSP 问题

一步转化。假设第 \(i\) 个时刻到达了第 \(j\) 个城市。那么这个 \(n\times n\) 的矩阵显然满足以下条件：

• 每行只能有一个神经元“开启”。

• 每列只能有一个神经元“开启”。

• 对于 \(n\) 个城市的问题，将开启 \(n\) 个神经元。

\[\begin{aligned} E & =\underbrace{\frac{\lambda_1}{2} \sum_{i=1}^n \sum_{x=1}^n \sum_{y=1}^n s_{x i} d_{x y}\left(s_{y, i-1}+s_{y, i+1}\right)}_{\text {goal }} \\ & +\underbrace{\frac{\lambda_2}{2} \sum_{x=1}^n \sum_{i=1}^n \sum_{j=1}^n s_{x i} s_{x j}+\frac{\lambda_3}{2} \sum_{i=1}^n \sum_{x=1}^n \sum_{y=1}^n s_{x i} s_{y i}+\frac{\lambda_4}{2}\left(\sum_{x=1}^n \sum_{i=1}^n s_{x i}-n\right)^2}_{\text {constraint }} \end{aligned} \]

上课也没讲后续怎么做，什么拉格朗日乘子法什么玩意的，或者是经过一些奥妙重重的方式把 TSP 的势能函数抽象出来，总之是没懂。留点儿公式吧。

\[\begin{gathered} E=-\frac{1}{2} \sum_{i=0}^n \sum_{j=0}^n \omega_{i j} s_i s_j-\sum_{i=1}^n I_i s_i \\ E=-\frac{1}{2} \sum_{x=1}^n \sum_{i=1}^n \sum_{y=1}^n \sum_{j=1}^n s_{x i} \omega_{x i, y j} s_{y j}-\frac{1}{2} \sum_{x=1}^n \sum_{i=1}^n I_{x i} s_{x i} \\ \omega_{x i, y j}=-\lambda_1 d_{x y}\left(\delta_{i, j+1}+\delta_{i, j-1}\right)-\lambda_2 \delta_{x y}\left(1-\delta_{i j}\right)-\lambda_3 \delta_{i j}\left(1-\delta_{x y}\right)-\lambda_4\left(1-\delta_{i j}\right)\left(1-\delta_{x y}\right) \\ I_{x i}=\lambda_4 n \quad \delta_{x y}=\left\{\begin{array}{l} 1, x=y \\ 0, x \neq y \end{array}\right. \end{gathered} \]

LSTM

看不懂啦

SOFM 自组织特征映射

Self-Organizing Feature Map (SOFM) of Kohonen ，一种无监督学习的神经网络，用于降维的同时保存数据的拓扑信息，属于竞争学习的范畴。SOFM 通常将高维输入映射到一维或二维的输出空间中。在这个映射过程中，它保持了输入数据的拓扑结构，即相似的输入数据在映射后的空间中仍然保持相似性。

e.g. 对人进行建模。打标签的方式，可以用 SOFM 降维。

三大原则

• 自我强化 (Self-organization):

  • SOFM 的自我组织能力指的是网络在没有外部干预的情况下，通过内部机制形成有组织的结构。这是通过逐渐调整神经元权重实现的，使得相似的输入会激活相邻的神经元。

• 竞争（Competition）:

  • 在每次迭代中，所有神经元会竞争对当前输入向量的响应。最终，仅有一个（或一小组）神经元成为赢家，即所谓的“胜者通吃”原则。

• 协同 (Cooperation):

  • 获胜的神经元不仅会调整自己的权重来更好地匹配输入，还会影响其邻近神经元的权重，从而在网络中形成局部的拓扑结构。

最后形成的局面会长这样，是以上全部特性共同缔造的结果。

应用

SOFM 应用广泛，包括数据可视化、模式识别、分类和聚类分析等领域。通过SOFM，复杂或高维的数据可以以更直观的方式被展现和解释。