强化学习学习笔记（第四章，动态规划）

本章的重点就是计算价值函数，通过DP进行迭代计算。

Vπ(s)的定义式：

 

 

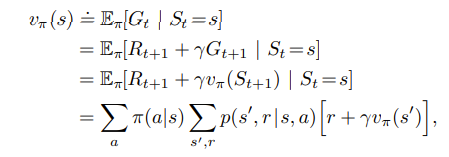
 迭代计算方式：

 

 

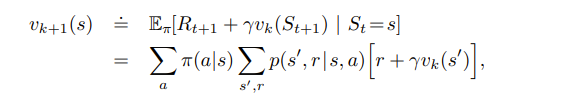
 以该问题为例，编写代码加深理解：

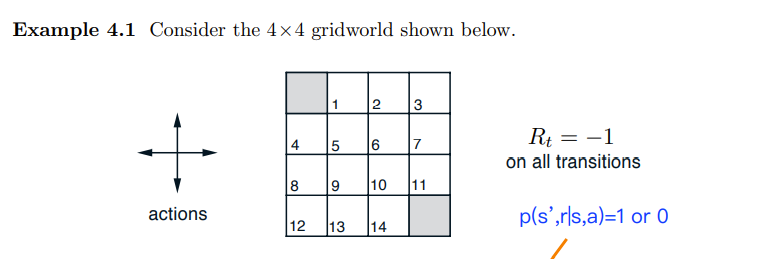
过程图：

 

 

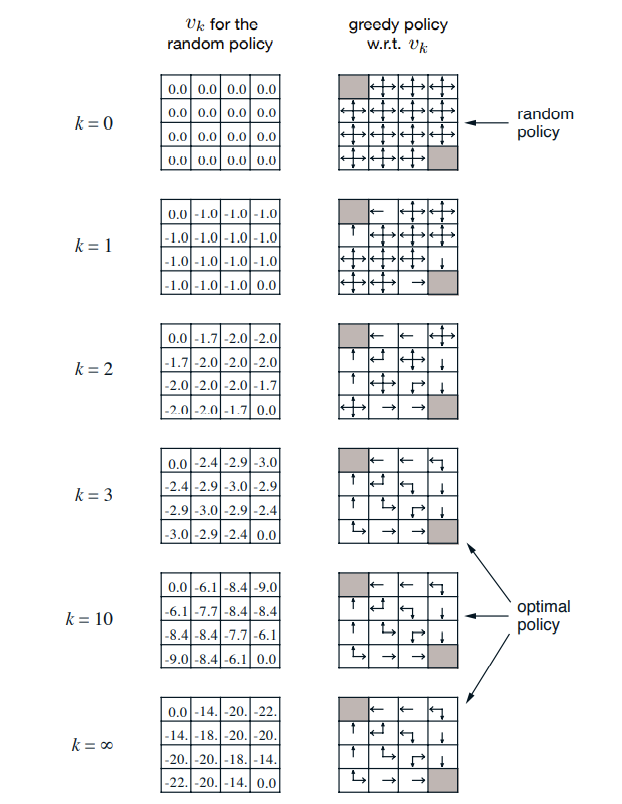
本图中展示的是策略不变的情况。虽然策略没变，但是仍然找到了每个状态的最优动作。

 

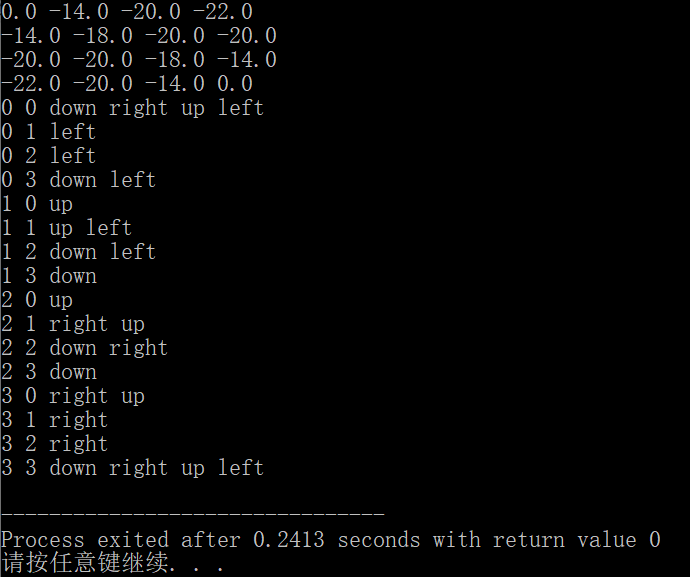
 此为模拟程序在策略不改变的情况下展示的结果

策略改变：

 

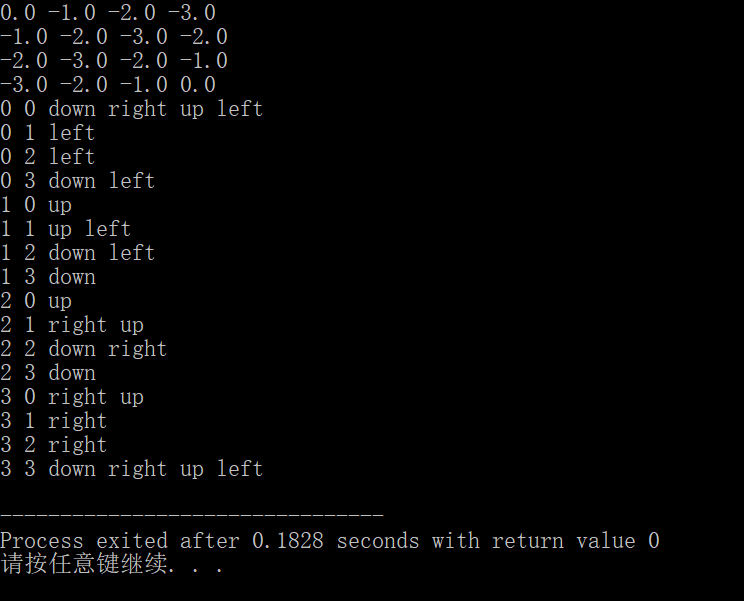
 添加了基于贪心的策略改进之后，Vπ比原来更优。

代码：

#include <bits/stdc++.h>
using namespace std;
double eps = 1e-10;
double v[2][5][5];//v(s)
double q[5][5][5];//q(s,a) 
double pi[5][5][5]; //π 
int dx[4] = {1, 0, -1, 0}, dy[4] = {0, 1, 0, -1};

void print(int x) {
	if(x == 0) printf("down ");
	if(x == 1) printf("right ");
	if(x == 2) printf("up ");
	if(x == 3) printf("left "); 
}

int pos(int x, int y) {
	return (x - 1) * 4 + y;
}

int p(int x) {
	if(x < 0) return 0;
	if(x > 3) return 3;
	return x;
}
void solve(int k) {
	int now = k & 1;
	int pre = now ^ 1;
	memset(v[now], 0, sizeof(v[now]));
	//迭代 
	for (int i = 1; i < 15; i++) {
		int x = i / 4, y = i % 4;
		for (int j = 0; j < 4; j++) {
			int tx = p(x + dx[j]), ty = p(y + dy[j]);
			q[x][y][j] = pi[x][y][j] * (v[pre][tx][ty] - 1.0);
			if(q[x][y][j] == 0) q[x][y][j] = -1e9; 
			v[now][x][y] += pi[x][y][j] * (v[pre][tx][ty] - 1.0);
		}
	}
	//策略改进 
	vector<int> tmp;
	for (int i = 0; i < 4; i++) {
		for (int j = 0; j < 4; j++) {
			double mx = -1e9;
			tmp.clear();
			for (int k = 0;  k < 4; k++) {
				if(q[i][j][k] - mx > eps) {
					mx = q[i][j][k];
					tmp.clear();
					tmp.push_back(k);
				}
				else if(fabs(q[i][j][k] - mx) < eps) {
					tmp.push_back(k);
				}
			}
//			printf("%d %d ", i, j);
			memset(pi[i][j], 0, sizeof(pi[i][j]));
			for (auto x : tmp) {
				pi[i][j][x] = 1.0 / tmp.size();
			}
//			printf("\n");
		}
	}
}

void print_table(int now) {
	for (int i = 0; i < 4; i++) {
		for (int j = 0; j < 4; j++) {
			printf("%.1lf ", v[now][i][j]);
		}
		printf("\n");
	}
	vector<int> tmp;
	for (int i = 0; i < 4; i++) {
		for (int j = 0; j < 4; j++) {
			double mx = -1e9;
			tmp.clear();
			for (int k = 0;  k < 4; k++) {
				if(q[i][j][k] - mx > eps) {
					mx = q[i][j][k];
					tmp.clear();
					tmp.push_back(k);
				}
				else if(fabs(q[i][j][k] - mx) < eps) {
					tmp.push_back(k);
				}
			}
			printf("%d %d ", i, j);
			for (auto x : tmp) {
				print(x);
			}
			printf("\n");
		}
	}
}

int main() {
	int T = 1000;
	for (int i = 0; i < 5; i++) {
		for (int j = 0; j < 5; j++) {
			for (int k = 0; k < 5; k++) {
				pi[i][j][k] = 0.25;
			}
		}
	}
	for (int i = 1; i <= T; i++) {
		solve(i);
//		int now = T & 1;
//		print_table(now); 
	}
	int now = T & 1;
		print_table(now); 
}