2.3神经网络的“齿轮”：张量运算

神经网络学到的所有变换都可以简化为数值数据张量上的一些张量计算。

keras.layers.Dense(512, activation='relu')

这个层可以理解为一个函数，输入一个 2D 张量，返回另一个 2D 张量，即输入张量的新表示。具体而言，这个函数如下所示（其中 W 是一个 2D 张量，b 是一个向量，二者都是该层的属性）。

output = relu(dot(w,input)+b)

我们将上式拆开来看。这里有三个张量运算：输入张量和张量 W 之间的点积运算（dot）、得到的 2D 张量与向量 b 之间的加法运算（+）、最后的 relu 运算。relu(x) 是 max(x, 0)。

1.逐元素运算

relu运算和加法都是逐元素的运算。即该运算独立的应用于张量的每一个元素。这种运算非常适用于大规模并行实现。

例1：对逐元素relu运算的简单实现

#x是一个Numpy的2D张量
def naive_relu(x):
    assert len(x.shape)==2

#避免覆盖输入张量
x = x.copy()
for i in range(x.shape[0]):
    for j in range(x.shape[1]):
        x[i,j] = max(x[i,j], 0)
return x

例2：对加法采用同样的实现方法

def naive_add(x, y):
    assert len(x.shape)==2
    assert x.shape==y.shape
    
x = x.copy()
for i in range(x.shape[0]):
    for j in range(x.shape[1]):
        x[i,j] += y[i,j]
return x

根据同样的方法，你可以实现逐元素的乘法和减法等。

2.广播

如果将两个形状不同的张量相加，没有歧义的话，较小的张量将被广播，以匹配较大张量的形状。广播包含以下两步：

（1）向较小的张量添加轴（叫作广播轴），使其 ndim 与较大的张量相同。

（2）将较小的张量沿着新轴重复，使其形状与较大的张量相同。

例1：假设 X 的形状是 (32, 10)，y 的形状是 (10,)。首先，我们给 y添加空的第一个轴，这样 y 的形状变为 (1, 10)。然后，我们将 y 沿着新轴重复 32 次，这样得到的张量 Y 的形状为 (32, 10)，并且 Y[i, :] == y for i in range(0, 32)。现在，我们可以将 X 和 Y 相加，因为它们的形状相同。

注：在实际的实现过程中并不会创建新的张量，那样非常低效。重复的操作是虚拟的，它只会出现在算法中，而没有发生在内存中。

简单实现：

def naive_add_matrix_and_vector(x, y):
    assert len(x.shape) == 2 
    assert len(y.shape) == 1 
    assert x.shape[1] == y.shape[0]
    
 x = x.copy() 
 for i in range(x.shape[0]):
     for j in range(x.shape[1]):
         x[i, j] += y[j]
 return x

如果一个张量的形状是 (a, b, ... n, n+1, ... m)，另一个张量的形状是 (n, n+1,... m)，那么你通常可以利用广播对它们做两个张量之间的逐元素运算。广播操作会自动应用于从 a 到 n-1 的轴。

例：利用广播将逐元素的maximum运算应用于两个形状不同的张量

import numpy as np

x = np.random.random((64, 3, 32, 10)) 
y = np.random.random((32, 10)) 

#输出z的形状为（64,3,32,10），与x相同
z = np.maximum(x, y)

3.张量点积

 点积运算，也叫张量积。它将输入张量的元素合并在一起。在Numpy和keras中，用标准的dot运算符来实现点积。

import numpy as np
z = np.dot(x, y)

从数学角度来看，两个向量x,y的点积运算过程如下：

def naive_vector_dot(x,y):
    assert len(x.shape)==1
    assert len(y.shape)==1
    assert x.shape[0]==y.shape[0]
    
    z = 0.
    for i in range(x.shape[0]):
        z += x[i]*y[i]
    return z

注：两个向量之间的点积是一个标量，而且只有元素个数相同的向量之间才能做点积。

可以对一个矩阵 x 和一个向量 y 做点积，返回值是一个向量，其中每个元素是 y 和 x的每一行之间的点积。其实现过程如下。

import numpy as np
def naive_matrix_vector_dot(x, y):
    assert len(x.shape) == 2 
    assert len(y.shape) == 1 
    assert x.shape[1] == y.shape[0] 
    
    z = np.zeros(x.shape[0]) 
    for i in range(x.shape[0]):
        for j in range(x.shape[1]):
            z[i] += x[i, j] * y[j]
    return z

复用前面的代码，实现过程：

import numpy as np


def naive_matrix_vector_dot(x, y):
    z = np.zeros(x.shape[0])
    for i in range(x.shape[0]):
        z[i] = naive_vector_dot(x[i, :], y)
    return z

点积可以推广到具有任意个轴的张量。最常见的应用可能就是两个矩阵之间的点积。对于两个矩阵 x 和 y，当且仅当 x.shape[1] == y.shape[0] 时，你才可以对它们做点积（dot(x, y)）。得到的结果是一个形状为 (x.shape[0], y.shape[1]) 的矩阵，其元素为 x的行与 y 的列之间的点积。其简单实现如下。

def naive_matrix_dot(x, y):
    assert len(x.shape) == 2 
    assert len(y.shape) == 2
    assert x.shape[1] == y.shape[0] 
    
    z = np.zeros((x.shape[0], y.shape[1])) 
    for i in range(x.shape[0]): 
        for j in range(y.shape[1]): 
            row_x = x[i, :]
            column_y = y[:, j]
            z[i, j] = naive_vector_dot(row_x, column_y)
    return z

可视化理解点积的形状匹配：

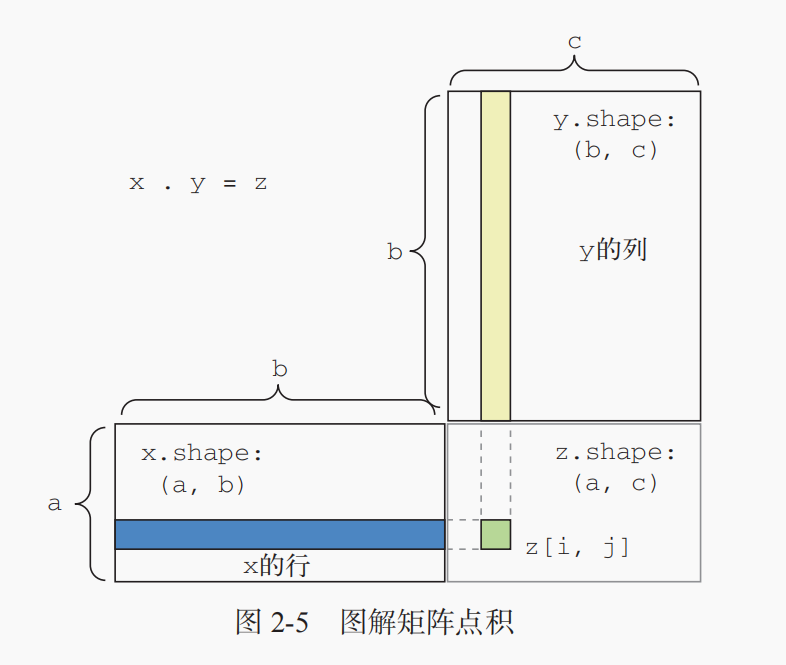
更一般地说，你可以对更高维的张量做点积，只要其形状匹配遵循与前面 2D 张量相同的原则：

(a, b, c, d) . (d,) -> (a, b, c)

(a, b, c, d) . (d, e) -> (a, b, c, e)

4.张量变形

张量变形是指改变张量的行和列，以得到想要的形状。变形后的张量的元素总个数与初始张量相同。

 例1：

import numpy as np

x = np.array([[1, 2],
              [3, 4],
              [5, 6]])

print(x.shape)

x1 = x.reshape((6, 1))
print(x1)

x2 = x.reshape((2, 3))
print(x2)

经常遇到的一种特殊的张量变形是转置（transposition）。对矩阵做转置是指将行和列互换，使 x[i, :] 变为 x[:, i]。

import numpy as np

x = np.array([[1, 2],
              [3, 4],
              [5, 6]])

print(x.shape)

x1 = x.transpose()
#x1 = np.transpose(x)
print(x1.shape)

 

 5.张量运算的几何解释

对于张量运算所操作的张量，其元素可以被解释为某种几何空间内点的坐标，因此所有的张量运算都有几何解释。

 例1：首先有这样一个向量A=[0.5, 1],再假设有这么一个向量B=[1, 0.25],计算A+B

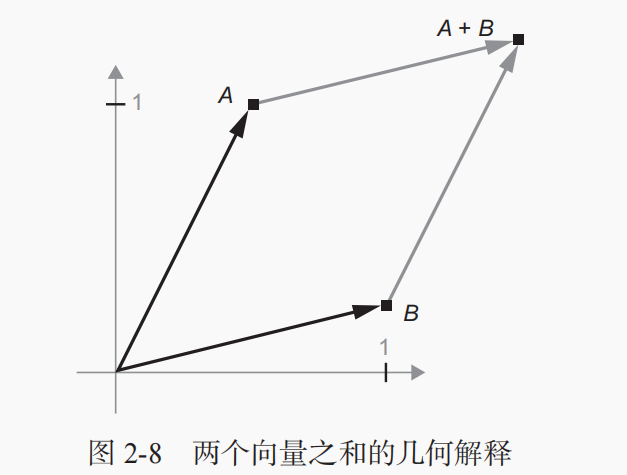
通常来说，仿射变换、旋转、缩放等基本的几何操作都可以表示为张量运算。举个例子，要将一个二维向量旋转 theta 角，可以通过与一个 2×2 矩阵做点积来实现，这个矩阵为 R = [u, v]，其中 u 和 v 都是平面向量：u = [cos(theta), sin(theta)]，v = [-sin(theta), cos(theta)]。

6.深度学习的几何解释

可以将神经网络解释为高维空间中非常复杂的几何变换，这种变换可以通过许多简单的步骤来实现。

例：想象有两张彩纸：一张红色，一张蓝色。36　　第 2 章　神经网络的数学基础将其中一张纸放在另一张上。现在将两张纸一起揉成小球。这个皱巴巴的纸球就是你的输入数据，每张纸对应于分类问题中的一个类别。神经网络（或者任何机器学习模型）要做的就是找到可以让纸球恢复平整的变换，从而能够再次让两个类别明确可分。通过深度学习，这一过程可以用三维空间中一系列简单的变换来实现，比如你用手指对纸球做的变换，每次做一个动作，如图 2-9 所示。

 

让纸球恢复平整就是机器学习的内容：为复杂的、高度折叠的数据流形找到简洁的表示。现在你应该能够很好地理解，为什么深度学习特别擅长这一点：它将复杂的几何变换逐步分解为一长串基本的几何变换，这与人类展开纸球所采取的策略大致相同。深度网络的每一层都通过变换使数据解开一点点——许多层堆叠在一起，可以实现非常复杂的解开过程。