双指针问题“转圈打印矩阵”+“之字型打印矩阵”+“在行列都排好序的矩阵中找数”+“回文问题”
转圈打印矩阵:
【题目】 给定一个整型矩阵matrix,请按照转圈的方式打印它。
例如:
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
打印结果为:1,2,3,4,8,12,16,15,14,13,9,5,6,7,11, 10
【要求】 额外空间复杂度为O(1)。
【思路】
模拟剥洋葱式输出,将矩阵从外围一圈一圈往里逼近。
设定两个标记位置,一个为矩阵的左上角边界,一个为矩阵的右下角边界,第一圈,从左上角的点开始按顺时针横坐标++打印元素,一直到右下角边界点的横坐标则停,然后纵坐标++往下打印元素,一直到右下角边界点的纵坐标则停,然后横坐标减减打印元素,一直到左上角边界点的横坐标则停,然后纵坐标减减输出打印,一直到与左上角边界点的纵坐标相等时不打印。此时即将外面一圈按转圈的方式打印完毕,然后更新左右边界,将左上角边界横纵坐标都++,右下角边界点横纵坐标都--,重复上述转圈打印,即可。
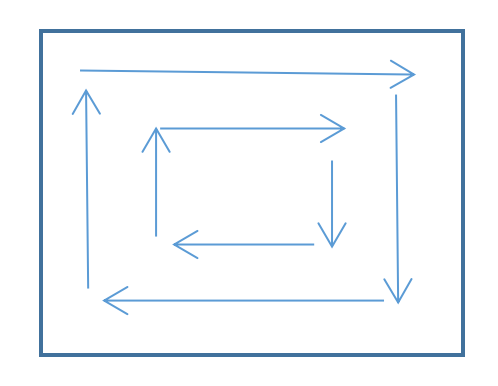
【Code】
public static void spiralOrderPrint(int[][] matrix) {
int tR = 0;//左上角坐标
int tC = 0;
int dR = matrix.length - 1;//右下角坐标
int dC = matrix[0].length - 1;
while (tR <= dR && tC <= dC) {
printEdge(matrix, tR++, tC++, dR--, dC--);
}
}
public static void printEdge(int[][] m, int tR, int tC, int dR, int dC) {
if (tR == dR) {
for (int i = tC; i <= dC; i++) {
System.out.print(m[tR][i] + " ");
}
} else if (tC == dC) {
for (int i = tR; i <= dR; i++) {
System.out.print(m[i][tC] + " ");
}
} else {
int curC = tC;
int curR = tR;
while (curC != dC) {
System.out.print(m[tR][curC] + " ");
curC++;
}
while (curR != dR) {
System.out.print(m[curR][dC] + " ");
curR++;
}
while (curC != tC) {
System.out.print(m[dR][curC] + " ");
curC--;
}
while (curR != tR) {
System.out.print(m[curR][tC] + " ");
curR--;
}
}
}
public static void main(String[] args) {
int[][] matrix = { { 1, 2, 3, 4 }, { 5, 6, 7, 8 }, { 9, 10, 11, 12 },
{ 13, 14, 15, 16 } };
spiralOrderPrint(matrix);
}
“之”字形打印矩阵:
【题目】 给定一个矩阵matrix,按照“之”字形的方式打印这个矩阵,
例如:
1 2 3 4
5 6 7 8
9 10 11 12
“之”字形打印的结果为:1,2,5,9,6,3,4,7,10,11,8,12
【要求】 额外空间复杂度为O(1)。
【思路】
设定两个点,初始位置都为(0,0),打印第一个元素后,a点往右移一步,b点往下移一步,两点之间形成一条对角线,打印对角线上的元素,规定方向,一开始为右上往左下,随后为左下往右上打印,打印完毕后两点继续右移和下移,当a点右移到边界时下移,b点下移到边界时右移,ab两点总能形成一条对角线,交替方向打印对角线上的数据即可。
【Code】
public static void printMatrixZigZag(int[][] matrix) {
int tR = 0;
int tC = 0;
int dR = 0;
int dC = 0;
int endR = matrix.length - 1;
int endC = matrix[0].length - 1;
boolean fromUp = false;
while (tR != endR + 1) {
printLevel(matrix, tR, tC, dR, dC, fromUp);
tR = tC == endC ? tR + 1 : tR;
tC = tC == endC ? tC : tC + 1;
dC = dR == endR ? dC + 1 : dC;
dR = dR == endR ? dR : dR + 1;
fromUp = !fromUp;
}
System.out.println();
}
public static void printLevel(int[][] m, int tR, int tC, int dR, int dC,
boolean f) {
if (f) {
while (tR != dR + 1) {
System.out.print(m[tR++][tC--] + " ");
}
} else {
while (dR != tR - 1) {
System.out.print(m[dR--][dC++] + " ");
}
}
}
在行列都排好序的矩阵中找数:
【题目】
给定一个有N*M的整型矩阵matrix和一个整数K,matrix的每一行和每一
列都是排好序的。实现一个函数,判断K是否在matrix中。
例如:
0 1 2 5
2 3 4 7
4 4 4 8
5 7 7 9
如果K为7,返回true;如果K为6,返回false。
【要求】
时间复杂度为O(N+M),额外空间复杂度为O(1)。
【思路】
依题意,起始先从矩阵的右上角开始查找,如果比K大,证明此点下方所有元素都比K大,不用再看,将位置左移,比较,若还是比K大,则证明此点下方所有元素也都比K大,不用再看,将位置左移,比较,若此时该位置比K小,但不等于K,则往下查,如又比K大,则左移,如比K小,则下移,直至查到,或到达矩阵边界,程序结束。
【Code】
public static boolean isContains(int[][] matrix, int K) {
int row = 0;
int col = matrix[0].length - 1;
while (row < matrix.length && col > -1) {
if (matrix[row][col] == K) {
return true;
} else if (matrix[row][col] > K) {
col--;
} else {
row++;
}
}
return false;
}
判断一个链表是否为回文结构:
【题目】
给定一个链表的头节点head,请判断该链表是否为回文结构。
例如:
1->2->1,返回true。
1->2->2->1,返回true。
15->6->15,返回true。
1->2->3,返回false。
附:查找链表中点位置,需要一个快指针和一个慢指针,快指针一次走两步,慢指针一次走1步,当快指针到达终点时慢指针即在链表的中点位置。
【基本思路】
使用一个栈结构,将数据都压入栈内,然后一一出栈与数组从头开始比较即可判别。
public static boolean isPalindrome1(Node head) {
Stack<Node> stack = new Stack<Node>();
Node cur = head;
while (cur != null) {
stack.push(cur);
cur = cur.next;
}
while (head != null) {
if (head.value != stack.pop().value) {
return false;
}
head = head.next;
}
return true;
}
进阶:
如果链表长度为N,时间复杂度达到O(N),额外空间复杂度达到O(1)。
【思路1】(省一半空间复杂度)
使用附中技术,找到链表中点,将中点后的元素都压入栈中,再依次从表头开始对出栈元素进行比较。
public static boolean isPalindrome2(Node head) {
if (head == null || head.next == null) {
return true;
}
Node right = head.next;
Node cur = head;
while (cur.next != null && cur.next.next != null) {
right = right.next;
cur = cur.next.next;
}
Stack<Node> stack = new Stack<Node>();
while (right != null) {
stack.push(right);
right = right.next;
}
while (!stack.isEmpty()) {
if (head.value != stack.pop().value) {
return false;
}
head = head.next;
}
return true;
}
【思路2】(空间复杂度为O(1)但实现较繁琐复杂,适合面试讲述)
还是用附的技术找到链表中点,此时将中点往后的元素进行逆序。然后从两头开始进行比对。
比如1->2->3->2->1,找到中点3,将3后的链表逆序,改成1->2->3<-2<-1,从两头进行比对,当任何一个指向空时停止。
逆序操作:例将3->2->1逆序,将2的next指针1记下,将2指向3,然后下顺,将1的next指针记下,再将next指向2。具体实现看Code。
【Code】
// need O(1) extra space
public static boolean isPalindrome3(Node head) {
if (head == null || head.next == null) {
return true;
}
Node n1 = head;
Node n2 = head;
while (n2.next != null && n2.next.next != null) { // find mid node
n1 = n1.next; // n1 -> mid
n2 = n2.next.next; // n2 -> end
}
n2 = n1.next; // n2 -> right part first node
n1.next = null; // mid.next -> null
Node n3 = null;
while (n2 != null) { // right part convert
n3 = n2.next; // n3 -> save next node
n2.next = n1; // next of right node convert
n1 = n2; // n1 move
n2 = n3; // n2 move
}
n3 = n1; // n3 -> save last node
n2 = head;// n2 -> left first node
boolean res = true;
while (n1 != null && n2 != null) { // check palindrome
if (n1.value != n2.value) {
res = false;
break;
}
n1 = n1.next; // left to mid
n2 = n2.next; // right to mid
}
n1 = n3.next;
n3.next = null;
while (n1 != null) { // recover list
n2 = n1.next;
n1.next = n3;
n3 = n1;
n1 = n2;
}
return res;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号