nchu-software-oop-2022-3
输入连个点的坐标,计算两点之间的距离
输入格式:
4个double类型的实数,两个点的x,y坐标,依次是x1、y1、x2、y2,两个点的坐标之间以空格分隔,每个点的x,y坐标以英文“,”分隔。例如:0,0 1,1或0.1,-0.3 +3.5,15.6。
若输入格式非法,输出"Wrong Format"。
若输入格式合法但坐标点的数量超过两个,输出“wrong number of points”。
输出格式:
计算所得的两点之间的距离。例如:1.4142135623730951
输入样例:
整数输入。例如:
0,0 1,1输出样例:
在这里给出相应的输出。例如:
1.4142135623730951输入样例1:
带符号double类型实数输入。例如:
+2,-2.3 0.9,-3.2输出样例1:
在这里给出相应的输出。例如:
1.42126704035519输入样例2:
格式非法。例如:
++2,-2.3 0.9,-3.2输出样例2:
在这里给出相应的输出。例如:
Wrong Format输入样例3:
点的数量超过两个。例如:
+2,-2.3 0.9,-3.2 +2,-2.3输出样例3:
在这里给出相应的输出。例如:
wrong number of points从这里开始就明显需要正则表达式判定输入了,因为非法输入的情况太多了,使用正则表达式判定是最简单快捷的方式。我使用的正则表达式是"([+|-]?)(0|[1-9](\\d*))(\\.\\d+)?",可以判定一个合法数字的输入。但是输入样例都是点集,所以不能直接对输入的字符串进行判定。我需要使用String.split("")进行分割,我选择先对输入的字符串对空格进行分割,这样我可以得到两个点的字符串数组,一个是空格前面的点,一个是空格后面的一个点。但是这样还是无法利用正则表达式判定,所以我需要对于单个点对','进行分割,即我可以得到一个x和一个y。这样我就可以对x或者y进行合法判定。如果嫌麻烦的同学也可以将正则表达式改成可以直接判定输入点集的表达式。如果我对空格分割的数组长度大于2,则输出wrong number of points”,如果合法按照公式输出两点之间距离即可。核心代码如下:
String s0="([+|-]?)(0|[1-9](\\d*))(\\.\\d+)?";
String[] str=s1.split(" ");
for(int i=0;i<str.length;i++)
{
String[] str1=str[i].split(",");
p[i]=new point();
if(str1[0].matches(s0)&&str1[1].matches(s0))
{
p[i].x=Double.parseDouble(str1[0]);
p[i].y=Double.parseDouble(str1[1]);
}
else
{
System.out.println("Wrong Format");
return;
}
cnt++;
}
if(cnt>2)
{
System.out.println("wrong number of points");
return;
}
else
{
System.out.println(Math.sqrt(Math.pow(p[0].x-p[1].x,2)+Math.pow(p[0].y-p[1].y,2)));
}
}这里提一嘴,按正则表达式匹配字符串应该使用String.match(regexp)。
用户输入一组选项和数据,进行与直线有关的计算。选项包括:
1:输入两点坐标,计算斜率,若线条垂直于X轴,输出"Slope does not exist"。
2:输入三个点坐标,输出第一个点与另外两点连线的垂直距离。
3:输入三个点坐标,判断三个点是否在一条线上,输出true或者false。
4:输入四个点坐标,判断前两个点所构成的直线与后两点构成的直线是否平行,输出true或者false.
5:输入四个点坐标,计算输出前两个点所构成的直线与后两点构成的直线的交点坐标,x、y坐标之间以英文分隔",",并输出交叉点是否在两条线段之内(不含四个端点)的判断结果(true/false),判断结果与坐标之间以一个英文空格分隔。若两条线平行,没有交叉点,则输出"is parallel lines,have no intersection point"。
输入格式:
基本格式:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。
例如:1:0,0 1,1
如果不符合基本格式,输出"Wrong Format"。
如果符合基本格式,但输入点的数量不符合要求,输出"wrong number of points"。
不论哪个选项,如果格式、点数量都符合要求,但构成任一条线的两个点坐标重合,输出"points coincide",
输出格式:
见题目描述。
输入样例1:
选项1,两点重合。例如:
1:-2,+5 -2,+5输出样例:
在这里给出相应的输出。例如:
points coincide输入样例2:
选项1,斜率无穷大的线。例如:
1:-2,3 -2,+5输出样例:
在这里给出相应的输出。例如:
Slope does not exist输入样例3:
选项1,斜率无穷大。例如:
1:-2,3 -2,+5输出样例:
在这里给出相应的输出。例如:
Slope does not exist输入样例4:
选项1,符合格式输入,带符号/不带符号数混合。例如:
1:-2.5,3 -2,+5.3输出样例:
在这里给出相应的输出。例如:
4.6输入样例5:
选项2,计算第一个点到另外两点连线的垂直距离。例如:
2:0,1 1,0 2,0输出样例:
在这里给出相应的输出。例如:
1.0输入样例6:
选项3,判断三个点是否在一条线上。例如:
3:0,1 2,2 5,3输出样例:
在这里给出相应的输出。例如:
false输入样例7:
选项4,判断两条线是否平行。例如:
4:0,1 0,2 2,1 3,0 输出样例:
在这里给出相应的输出。例如:
false输入样例8:
选项5,判断两条线的交点。例如:
5:0,0 -1,-1 0,2 3,-1输出样例:
在这里给出相应的输出,交点坐标之间以英文","分隔,判断结果与坐标之间以一个英文空格分隔。例如:
1.0,1.0 true输入样例9:
选项5,判断两条线的交点。但两条线平行例如:
5:0,0 -1,-1 2,3 3,4输出样例:
在这里给出相应的输出,交点坐标之间以英文","分隔,判断结果与坐标之间以一个英文空格分隔。例如:
is parallel lines,have no intersection point这题我们需要先使用正则表达式去判定输入的合法性,可以使用"^\\d:(.*)"进行判定,但是后面switch中需要加入default的情况,也就是序号不在1-5的范围内的情况。或者干脆直接使用"^[1-5]:(.*)"判定,将范围限制在1-5之间。点的判定同上一题,你也可以选择将点和序号判定合起来。接下来就是按照序号实现功能了,在每个功能的实现前都需要判断点的个数是否和要求相等,如果数量都不相等,直接输出"wrong number of points",其次就是判断构成线的两点是否重合,可以把这个判定重合封装进点的类里。唯一值得一提的是选项5,如果需要判定交点是否在线段内,可以线判定两条直线是否平行,如果平行则输出"is parallel lines,have no intersection point"。不平行的情况下,通过交点坐标公式求出交点,如果交点的x在4个点x的内部,即x小于第一条线两点中最大的x坐标并且大于最小的x点坐标,y和另一条直线同理。核心代码如下:
class cal{
double test1(point p1,point p2){
double a=(p1.x-p2.x)/(p1.y-p2.y);
return a;
}
double test2(point p1,point p2,point p3){
double d=Math.abs(((p2.y-p3.y)*p1.x+(p3.x-p2.x)*p1.y+p2.x*p3.y-p2.y*p3.x)/Math.sqrt(Math.pow((p2.y-p3.y),2)+Math.pow((p2.x-p3.x),2)));
return d;
}
boolean test3(point p1,point p2,point p3){
double a=(p1.x-p2.x)/(p1.y-p2.y);
if(a!=0){
double b=p1.y-(1/a)*p1.x;
if(p3.y==(1/a)*p3.x+b)
return true;
else
return false;
}
else{
if(p1.x==p2.x&&p1.x==p3.x)
return true;
else
return false;
}
}
boolean test4(point p1,point p2,point p3,point p4){
double a1,a2;
if(p1.y-p2.y==0||p3.y-p4.y==0){
a1=(p1.y-p2.y)/(p1.x-p2.x);
a2=(p3.y-p4.y)/(p3.x-p4.x);
}
else{
a1=(p1.x-p2.x)/(p1.y-p2.y);
a2=(p3.x-p4.x)/(p3.y-p4.y);
}
if(a1==a2)
return true;
else
return false;
}
void test5(point p1,point p2,point p3,point p4){
double a=((p1.x-p2.x)*(p3.x*p4.y-p4.x*p3.y)-(p3.x-p4.x)*(p1.x*p2.y-p2.x*p1.y))/((p3.x-p4.x)*(p1.y-p2.y)-(p1.x-p2.x)*(p3.y-p4.y));
double b=((p1.y-p2.y)*(p3.x*p4.y-p4.x*p3.y)-(p1.x*p2.y-p2.x*p1.y)*(p3.y-p4.y))/((p3.x-p4.x)*(p1.y-p2.y)-(p1.x-p2.x)*(p3.y-p4.y));
System.out.print(a);
System.out.print(',');
System.out.print(b);
System.out.print(" ");
if((a<Math.max(p1.x,p2.x)&&a>Math.min(p1.x,p2.x)&&a<Math.max(p1.y,p2.y)&&a>Math.min(p1.y,p2.y))||(b<Math.max(p3.x,p4.x)&&b>Math.min(p3.x,p4.x)&&b<Math.max(p3.y,p4.y)&&b>Math.min(p3.y,p4.y)))
{
System.out.print("true");
}
else
System.out.print("false");
}
用户输入一组选项和数据,进行与三角形有关的计算。选项包括:
1:输入三个点坐标,判断是否是等腰三角形、等边三角形,判断结果输出true/false,两个结果之间以一个英文空格符分隔。
2:输入三个点坐标,输出周长、面积、重心坐标,三个参数之间以一个英文空格分隔,坐标之间以英文","分隔。
3:输入三个点坐标,输出是钝角、直角还是锐角三角形,依次输出三个判断结果(true/false),以一个英文空格分隔,
4:输入五个点坐标,输出前两个点所在的直线与三个点所构成的三角形相交的交点数量,如果交点有两个,则按面积大小依次输出三角形被直线分割成两部分的面积。若直线与三角形一条线重合,输出"The point is on the edge of the triangle"
5:输入四个点坐标,输出第一个是否在后三个点所构成的三角形的内部(输出in the triangle/outof triangle)。
必须使用射线法,原理:由第一个点往任一方向做一射线,射线与三角形的边的交点(不含点本身)数量如果为1,则在三角形内部。如果交点有两个或0个,则在三角形之外。若点在三角形的某条边上,输出"on the triangle"
输入格式:
基本格式:选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔,点与点之间以一个英文空格分隔。
输出格式:
基本输出格式见每种选项的描述。
异常情况输出:
如果不符合基本格式,输出"Wrong Format"。
如果符合基本格式,但输入点的数量不符合要求,输出"wrong number of points"。
如果输入的三个点无法构成三角形,输出"data error"。
注意:输出的数据若小数点后超过6位,只保留小数点后6位,多余部分采用四舍五入规则进到最低位。小数点后若不足6位,按原始位数显示,不必补齐。例如:1/3的结果按格式输出为 0.333333,1.0按格式输出为1.0
选项4中所输入线的两个点坐标重合,输出"points coincide",
输入样例1:
选项4,定义线的两点重合。例如:
4:1,0 1,0 0,0 2,0 4,0输出样例:
在这里给出相应的输出。例如:
points coincide输入样例2:
选项4,构成三角形的三个点在一条线上,无法构成三角形。例如:
4:1,0 0,2 0,0 0,0 4,0输出样例:
在这里给出相应的输出。例如:
data error输入样例3:
选项1,判断等腰、等边三角形。例如:
1:-2,0 2,0 0,4输出样例:
两个判断结果。例如:
true false输入样例4:
选项2,输出边长、面积、重心坐标。例如:
2:0,0 3,0 0,1输出样例:
在这里给出相应的输出。例如:
7.162278 1.5 1.0,0.333333输入样例5:
选项3,钝角、直角、锐角的判断。例如:
3:0,1 1,0 2,0输出样例:
在这里给出相应的输出。例如:
true false false输入样例6:
选项4,直线与三角形交点的数量等于2,输出数量值以及三角形被分割的两部分面积。例如:
4:1,0 0,2 0,0 0,2 4,0输出样例:
在这里给出相应的输出。例如:
2 1.0 3.0输入样例7:
选项4,直线与三角形交点的数量少于两个,只输出数量值。例如:
4:-1,0 1,2 0,1 0,-1 2,0输出样例:
在这里给出相应的输出。例如:
1输入样例8:
选项5,用射线法判断点是否在三角形内部。例如:
5:0.5,0.5 0,0 0,2 4,0输出样例:
在这里给出相应的输出,交点坐标之间以英文","分隔,判断结果与坐标之间以一个英文空格分隔。例如:
in the triangle输入样例9:
选项5,用射线法判断点是否在三角形内部。例如:
5:0,0 -1,-1 2,3 3,4输出样例:
在这里给出相应的输出。例如:
outof the triangle这题合法输入条件与上一题相同,主要的难点可能在于按照选项实现功能,以及实现精度问题。精度问题其实很好实现,我所使用的方式是先将double类型数据转换为字符串,利用String.substring(String.indexOf(".")+1)进行切割,实际上就是将double类型小数点后的数据切割完保存在一个字符串内,这样的话如果我想知道小数点后是否超过6位,我可以直接对字符串求长度得知。相关代码如下:
void accuracy(double a){
String s=Double.toString(a);
String str=s.substring(s.indexOf(".")+1);
if(str.length()>6)
System.out.printf("%.6f",a);
else
System.out.print(a);
}选项1的实现还是比较简单的,之前的题目也曾实现过。只需要通过坐标算出边长,判断边长相等就可以分别判断出是等腰还是直角三角形。选项二周长直接通过第一问求得的边长a+b+c即可求得。面积的求法如果使用边长可能稍显麻烦,如果学过线性代数可以知道通过三角形三点坐标可以直接求得面积的 ,S=Math.abs(0.5*((p1.x*p2.y-p2.x*p1.y)+(p2.x*p3.y-p3.x*p2.y)+(p3.x*p1.y-p1.x*p3.y)))。重心坐标((x1+x2+x3)/3,(y1+y2+y3)/3)。选项3的实现,如果a*a>b*b+c*c就可以说明是钝角三角形,a*a<b*b+c*c则说明是锐角三角形。但是如果你直接这么判定还是会有一个测试样例无法通过,这是因为这也存在精度问题,无法做到精准的判定相等。所以如果我们需要判定他是否为钝角三角形a*a-(b*b+c*c)>1e-6需要这么判定。选项4我们要分情况讨论,如果前面两点构成的直线和任意一边平行,我们判定交点时就可以少判定一条边相交的情况。输出面积的话,可以通过大三角形减去小三角形面积的方式求得,这样就可以避免计算四边形面积。选项5需要注意的是,如果你从三角形外引入一个点构成直线和三角形判断交点的话,你需要注意必须是射线,所以交点必须要在给定点的一侧,也就是不是所有交点都满足条件。核心代码如下:
class Triangle{
boolean judge(point p1,point p2,point p3){
double a,b,c;
a=Math.sqrt(Math.pow((p1.x-p2.x),2)+Math.pow((p1.y-p2.y),2));
b=Math.sqrt(Math.pow((p1.x-p3.x),2)+Math.pow((p1.y-p3.y),2));
c=Math.sqrt(Math.pow((p3.x-p2.x),2)+Math.pow((p3.y-p2.y),2));
if(a+b>c&&a+c>b&&b+c>a)
return true;
else
return false;
}
void test1(point p1,point p2,point p3){
double a,b,c;
a=Math.sqrt(Math.pow((p1.x-p2.x),2)+Math.pow((p1.y-p2.y),2));
b=Math.sqrt(Math.pow((p1.x-p3.x),2)+Math.pow((p1.y-p3.y),2));
c=Math.sqrt(Math.pow((p3.x-p2.x),2)+Math.pow((p3.y-p2.y),2));
if(a==b||a==c||b==c)
System.out.print("true");
else
System.out.print("false");
System.out.print(" ");
if(a==b&&b==c&&a==c){
System.out.print("true");
}
else
System.out.print("false");
}
void test2(point p1,point p2,point p3){
double a,b,c,C,S,x,y;
a=Math.sqrt(Math.pow((p1.x-p2.x),2)+Math.pow((p1.y-p2.y),2));
b=Math.sqrt(Math.pow((p1.x-p3.x),2)+Math.pow((p1.y-p3.y),2));
c=Math.sqrt(Math.pow((p3.x-p2.x),2)+Math.pow((p3.y-p2.y),2));
S=0.5*((p1.x*p2.y-p2.x*p1.y)+(p2.x*p3.y-p3.x*p2.y)+(p3.x*p1.y-p1.x*p3.y));
C=a+b+c;
x=(p1.x+p2.x+p3.x)/3;
y=(p1.y+p2.y+p3.y)/3;
accuracy(C);
System.out.print(" ");
accuracy(S);
System.out.print(" ");
accuracy(x);
System.out.print(",");
accuracy(y);
}
void test3(point p1,point p2,point p3){
double a,b,c;
a=Math.sqrt(Math.pow((p1.x-p2.x),2)+Math.pow((p1.y-p2.y),2));
b=Math.sqrt(Math.pow((p1.x-p3.x),2)+Math.pow((p1.y-p3.y),2));
c=Math.sqrt(Math.pow((p3.x-p2.x),2)+Math.pow((p3.y-p2.y),2));
if(a>=b&&a>=c){
if(a*a-(b*b+c*c)>1e-6)
System.out.print("true");
else
System.out.print("false");
System.out.print(" ");
if(Math.abs(a*a-(b*b+c*c))<1e-6)
System.out.print("true");
else
System.out.print("false");
System.out.print(" ");
if(a*a-(b*b+c*c)<-1e-6)
System.out.print("true");
else
System.out.print("false");
}
if(b>=a&&b>=c){
if(b*b-(a*a+c*c)>1e-6)
System.out.print("true");
else
System.out.print("false");
System.out.print(" ");
if(Math.abs(b*b-(a*a+c*c))<1e-6)
System.out.print("true");
else
System.out.print("false");
System.out.print(" ");
if(b*b-(a*a+c*c)<-1e-6)
System.out.print("true");
else
System.out.print("false");
}
if(c>=b&&c>=a){
if(c*c-(b*b+a*a)>1e-6)
System.out.print("true");
else
System.out.print("false");
System.out.print(" ");
if(Math.abs(c*c-(b*b+a*a))<1e-6)
System.out.print("true");
else
System.out.print("false");
System.out.print(" ");
if(c*c-(b*b+a*a)<-1e-6)
System.out.print("true");
else
System.out.print("false");
}
}
void test4(point p1,point p2,point p3,point p4,point p5){
line l1=new line(p1,p2);
line l2=new line(p3,p4);
line l3=new line(p3,p5);
line l4=new line(p4,p5);
double S=Area(p3,p4,p5),s1;
point p01=new point(),p02=new point(),p03=new point();
if(parallel(p1,p2,p3,p4)){
int cnt=0;
if(Test(p1,p2,p3,p5)){
cnt++;
p01=Test2(p1,p2,p3,p5);
}
if(Test(p1,p2,p4,p5)){
cnt++;
p02=Test2(p1,p2,p4,p5);
}
if(p01.x==p02.x&&p01.y==p02.y)
{
if(cnt>1)
cnt--;
}
if(cnt<2){
System.out.print(cnt);
return;
}
else{
System.out.print(cnt);
System.out.print(" ");
s1=Area(p5,p01,p02);
accuracy(Math.min(s1,S-s1));
System.out.print(" ");
accuracy(Math.max(s1,S-s1));
}
}
else if(parallel(p1,p2,p3,p5)){
int cnt=0;
if(Test(p1,p2,p3,p4)){
cnt++;
p01=Test2(p1,p2,p3,p4);
}
if(Test(p1,p2,p4,p5)){
cnt++;
p02=Test2(p1,p2,p4,p5);
}
if(p01.x==p02.x&&p01.y==p02.y)
{
if(cnt>1)
cnt--;
}
if(cnt<2){
System.out.print(cnt);
return;
}
else{
System.out.print(cnt);
System.out.print(" ");
s1=Area(p4,p01,p02);
accuracy(Math.min(s1,S-s1));
System.out.print(" ");
accuracy(Math.max(s1,S-s1));
}
}
else if(parallel(p1,p2,p4,p5)){
int cnt=0;
if(Test(p1,p2,p3,p4)){
cnt++;
p01=Test2(p1,p2,p3,p4);
}
if(Test(p1,p2,p3,p5)){
cnt++;
p02=Test2(p1,p2,p3,p5);
}
if(p01.x==p02.x&&p01.y==p02.y)
{
if(cnt>1)
cnt--;
}
if(cnt<2){
System.out.print(cnt);
return;
}
else{
System.out.print(cnt);
System.out.print(" ");
s1=Area(p3,p01,p02);
accuracy(Math.min(s1,S-s1));
System.out.print(" ");
accuracy(Math.max(s1,S-s1));
}
}
else{
int cnt=0;
if(Test(p1,p2,p3,p4)){
cnt++;
p01=Test2(p1,p2,p3,p4);
}
if(Test(p1,p2,p3,p5)){
cnt++;
p02=Test2(p1,p2,p3,p5);
}
if(Test(p1,p2,p4,p5)){
cnt++;
p03=Test2(p1,p2,p4,p5);
}
if(p01.x==p02.x&&p01.y==p02.y)
{
if(cnt>1)
cnt--;
}
if(p01.x==p03.x&&p01.y==p03.y)
{
if(cnt>1)
cnt--;
}
if(p02.x==p03.x&&p02.y==p03.y)
{
if(cnt>1)
cnt--;
}
if(cnt<2){
System.out.print(cnt);
return;
}
else{
System.out.print(cnt);
System.out.print(" ");
if(Test(p1,p2,p3,p4)&&Test(p1,p2,p3,p5)&&(Test2(p1,p2,p3,p4).x!=Test2(p1,p2,p3,p5).x||Test2(p1,p2,p3,p4).y!=Test2(p1,p2,p3,p5).y)){
s1=Area(p3,p01,p02);
accuracy(Math.min(s1,S-s1));
System.out.print(" ");
accuracy(Math.max(s1,S-s1));
}
else if(Test(p1,p2,p3,p4)&&Test(p1,p2,p4,p5)&&(Test2(p1,p2,p3,p4).x!=Test2(p1,p2,p4,p5).x||Test2(p1,p2,p3,p4).y!=Test2(p1,p2,p4,p5).y)){
s1=Area(p4,p01,p03);
accuracy(Math.min(s1,S-s1));
System.out.print(" ");
accuracy(Math.max(s1,S-s1));
}
else if(Test(p1,p2,p3,p5)&&Test(p1,p2,p4,p5)&&(Test2(p1,p2,p3,p5).x!=Test2(p1,p2,p4,p5).x||Test2(p1,p2,p3,p5).y!=Test2(p1,p2,p4,p5).y)){
s1=Area(p5,p02,p03);
accuracy(Math.min(s1,S-s1));
System.out.print(" ");
accuracy(Math.max(s1,S-s1));
}
}
}
}
void test5(point p1,point p2,point p3,point p4){
point p5=new point();
int sum=0;
p5.x=999;p5.y=999;
point p01=new point(),p02=new point(),p03=new point();
if(Test(p1,p5,p2,p3)){
p01=Test2(p1,p5,p2,p3);
}
if(Test(p1,p5,p2,p4)){
p02=Test2(p1,p5,p2,p4);
}
if(Test(p1,p5,p3,p4)){
p03=Test2(p1,p5,p3,p4);
}
int cnt=0;
if(p01.x<=Math.max(p2.x,p3.x)&&p01.x>=p1.x&&p01.y>=p1.y&&p01.y<=Math.max(p2.y,p3.y))
cnt++;
if(p02.x<=Math.max(p2.x,p4.x)&&p02.x>=p1.x&&p02.y>=p1.y&&p02.y<=Math.max(p2.y,p4.y))
cnt++;
if(p03.x<=Math.max(p3.x,p4.x)&&p03.x>=p1.x&&p03.y>=p1.y&&p03.y<=Math.max(p3.y,p4.y))
cnt++;
if(p01.x==p02.x&&p01.y==p02.y)
{
if(cnt>1)
cnt--;
}
if(p01.x==p03.x&&p01.y==p03.y)
{
if(cnt>1)
cnt--;
}
if(p03.x==p02.x&&p03.y==p02.y)
{
if(cnt>1)
cnt--;
}
if(cnt%2==1)
System.out.print("in the triangle");
else
System.out.print("outof the triangle");
}
boolean Test(point p1,point p2,point p3,point p4){
double a=((p1.x-p2.x)*(p3.x*p4.y-p4.x*p3.y)-(p3.x-p4.x)*(p1.x*p2.y-p2.x*p1.y))/((p3.x-p4.x)*(p1.y-p2.y)-(p1.x-p2.x)*(p3.y-p4.y));
double b=((p1.y-p2.y)*(p3.x*p4.y-p4.x*p3.y)-(p1.x*p2.y-p2.x*p1.y)*(p3.y-p4.y))/((p3.x-p4.x)*(p1.y-p2.y)-(p1.x-p2.x)*(p3.y-p4.y));
if((a<=Math.max(p3.x,p4.x)&&a>=Math.min(p3.x,p4.x)&&b<=Math.max(p3.y,p4.y)&&b>=Math.min(p3.y,p4.y)))
{
return true;
}
else
return false;
}
point Test2(point p1,point p2,point p3,point p4){
double a=((p1.x-p2.x)*(p3.x*p4.y-p4.x*p3.y)-(p3.x-p4.x)*(p1.x*p2.y-p2.x*p1.y))/((p3.x-p4.x)*(p1.y-p2.y)-(p1.x-p2.x)*(p3.y-p4.y));
double b=((p1.y-p2.y)*(p3.x*p4.y-p4.x*p3.y)-(p1.x*p2.y-p2.x*p1.y)*(p3.y-p4.y))/((p3.x-p4.x)*(p1.y-p2.y)-(p1.x-p2.x)*(p3.y-p4.y));
point p=new point();
p.x=a;
p.y=b;
return p;
}
double Area(point p1,point p2,point p3){
return Math.abs(0.5*((p1.x*p2.y-p2.x*p1.y)+(p2.x*p3.y-p3.x*p2.y)+(p3.x*p1.y-p1.x*p3.y)));
}
double distance(point p1,point p2,point p3){
double d=Math.abs(((p2.y-p3.y)*p1.x+(p3.x-p2.x)*p1.y+p2.x*p3.y-p2.y*p3.x)/Math.sqrt(Math.pow((p2.y-p3.y),2)+Math.pow((p2.x-p3.x),2)));
return d;
}
void accuracy(double a){
String s=Double.toString(a);
String str=s.substring(s.indexOf(".")+1);
if(str.length()>6)
System.out.printf("%.6f",a);
else
System.out.print(a);
}
boolean parallel(point p1,point p2,point p3,point p4){
line l1=new line(p1,p2);
line l2=new line(p3,p4);
if(l1.a==0){
if(l2.a==0&&l2.b%l1.b==l2.c%l1.c)
return true;
else
return false;
}
else if(l1.b==0){
if(l2.b==0&&l2.a%l1.a==l2.c%l1.c)
return true;
else
return false;
}
else{
if(l1.a%l1.b==l2.b%l2.a)
return true;
else
return false;
}
}
}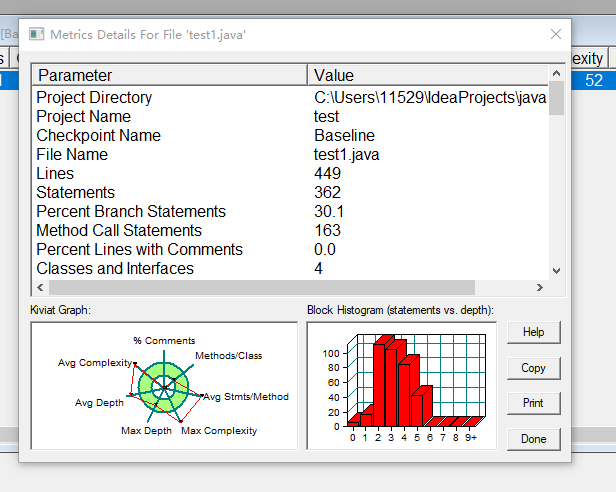
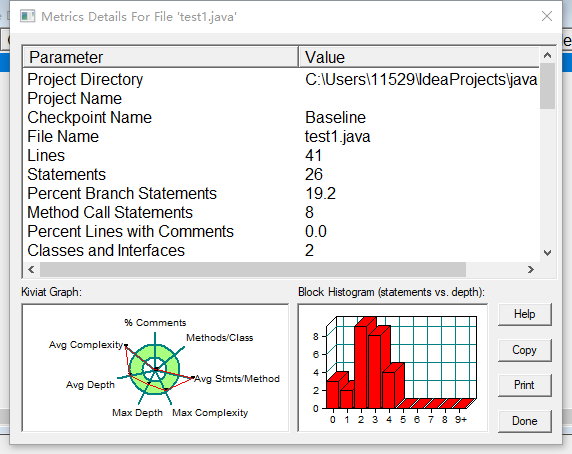
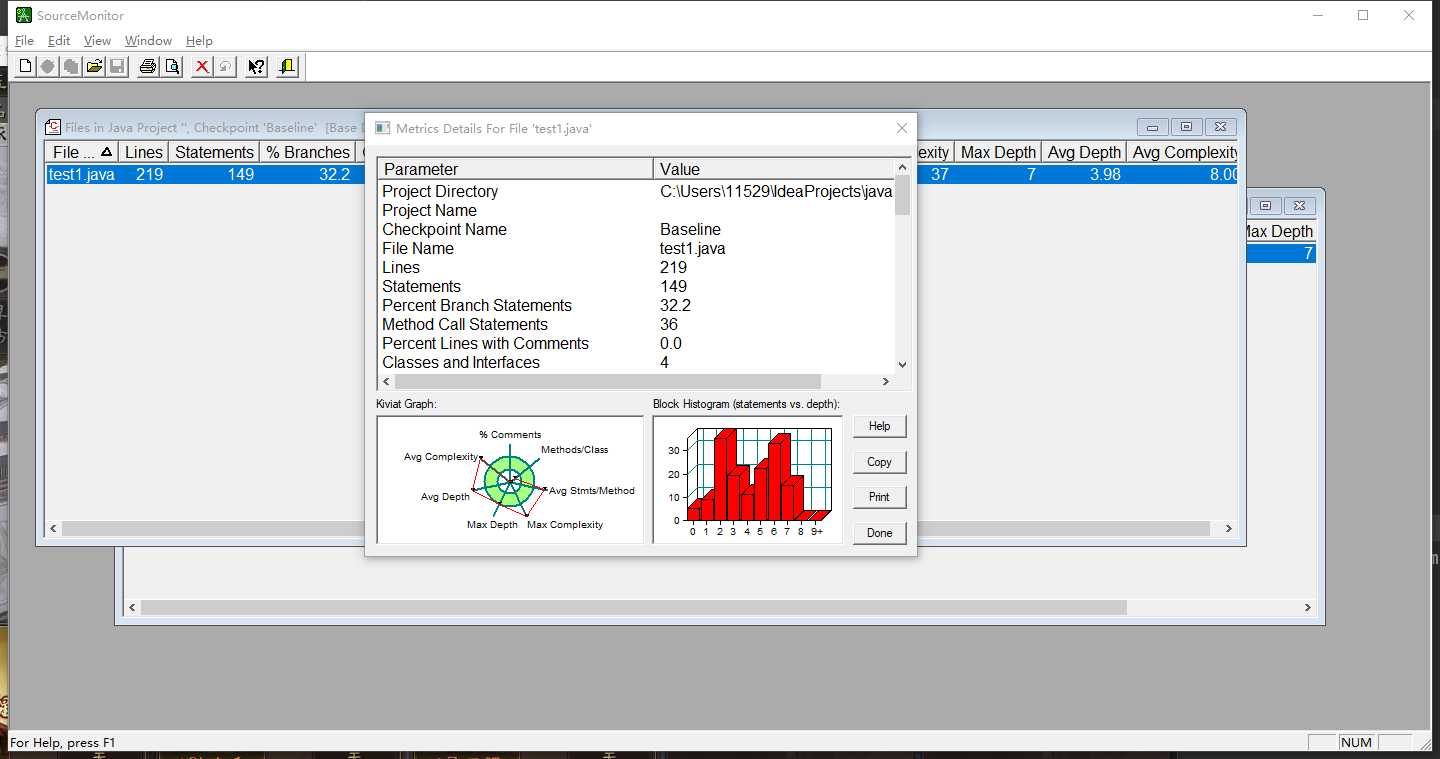
代码写的还是比较杂乱,有很多非必要的代码也在其中,因为写的时候思路不是很清晰。所以代码复杂度很高。
感谢观看!!!!!!





 浙公网安备 33010602011771号
浙公网安备 33010602011771号